Homework 3

Code

library(tidyverse)

knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)
library(ggplot2)

Introduction

For this Homework we will be exploring the Mass Public Schools dataset in more depth, and start to make some visualizations that investigate our main research questions which we outlined in the Homework 2.

Reading in Data

Code

data<- read_csv("_data/MA_Public_Schools_2017.csv",show_col_types = FALSE)

keeps <- c(1,2,10,13,14,15,26,27,28,29,30,31,32,34,36,38,40,42,43,44,45,46,47,48,49,50,51,53,55,62,64,68,70,71,72,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97)

hs <- data[keeps]%>% 
      subset(! is.na(data$`% Graduated`))

hs <- mutate(hs,
              `African American Students` = round((`% African American`/100)*`Number of Students`),
              `Asian Students` = round((`% Asian`/100)*`Number of Students`),
              `Hispanic Students` = round((`% Hispanic`/100)*`Number of Students`),
              `White Students` = round((`% White`/100)*`Number of Students`),
              `Native American Students` = round((`% Native American`/100)*`Number of Students`),
              `Native Hawaiian, Pacific Islander` = round((`% Native Hawaiian, Pacific Islander`/100)*`Number of Students`),
              `Multi-Race, Non-Hispanic` = round((`% Multi-Race, Non-Hispanic`/100)*`Number of Students`),
              `Male Students` = round((`% Males`/100)*`Number of Students`),
              `Female Students` = round((`% Females`/100)*`Number of Students`)
               )

Split Spending and Salary Into Brackets

The first research question we are interested in is how much of an effect teacher salary and spending on students plays a role in the success of students. Salaries can vary widely in the state and a question we would like to answer is whether or not teacher salary plays a role in the success of students, and whether or not there is a ceiling to which expenditures cease to produce better results.

First, mutate the data to include a “Salary Bracket” column and a “Enpenditure Bracket” column.

Code

hs <- mutate(hs,`Salary Bracket` = case_when(
            `Average Salary` < 55000 ~ "Less than $55000",
            `Average Salary` < 60000 ~ "Between $55000 and $60000",
            `Average Salary` < 65000 ~ "Between $60000 and $65000",
            `Average Salary` < 70000 ~ "Between $65000 and $70000",
            `Average Salary` < 75000 ~ "Between $70000 and $75000",
            `Average Salary` < 80000 ~ "Between $75000 and $80000",
            `Average Salary` < 85000 ~ "Between $80000 and $85000",
            `Average Salary` <= 90000 ~ "Between $85000 and $90000",
            `Average Salary` > 90000 ~ "Greater than $90000"
              ))

hs <- mutate(hs,`Per Pupil Expenditure Bracket` = case_when(
            `Average Expenditures per Pupil` < 12500 ~ "Less than $12500",
            `Average Expenditures per Pupil` < 15000 ~ "Between $12500 and $15000",
            `Average Expenditures per Pupil` < 17500 ~ "Between $15000 and $17500",
            `Average Expenditures per Pupil` < 20000 ~ "Between $17500 and $20000",
            `Average Expenditures per Pupil` < 22500 ~ "Between $20000 and $22500",
            `Average Expenditures per Pupil` <= 25000 ~ "Between $22500 and $25000",
            `Average Expenditures per Pupil` > 25000 ~ "Greater than $25000"
              ))

Before we dive into the data, let’s take a look at two scatter plots for Salary and average expenditures to see if anything sticks out.

Code

ggplot(hs, aes(x=`Average Expenditures per Pupil`, y=`% Graduated`)) + geom_point()+
  theme_bw() +
  labs(title ="Per Pupil Expenditure vs Graduation Rate", y = "Graduation Rate", x = "Average Expenditure per Pupil")

Code

ggplot(hs, aes(x=`Average Salary`, y=`% Graduated`)) + geom_point()+
  theme_bw() +
  labs(title ="Average Teacher Salary vs Graduation Rate", y = "Graduation Rate", x = "Average Teacher Salary")

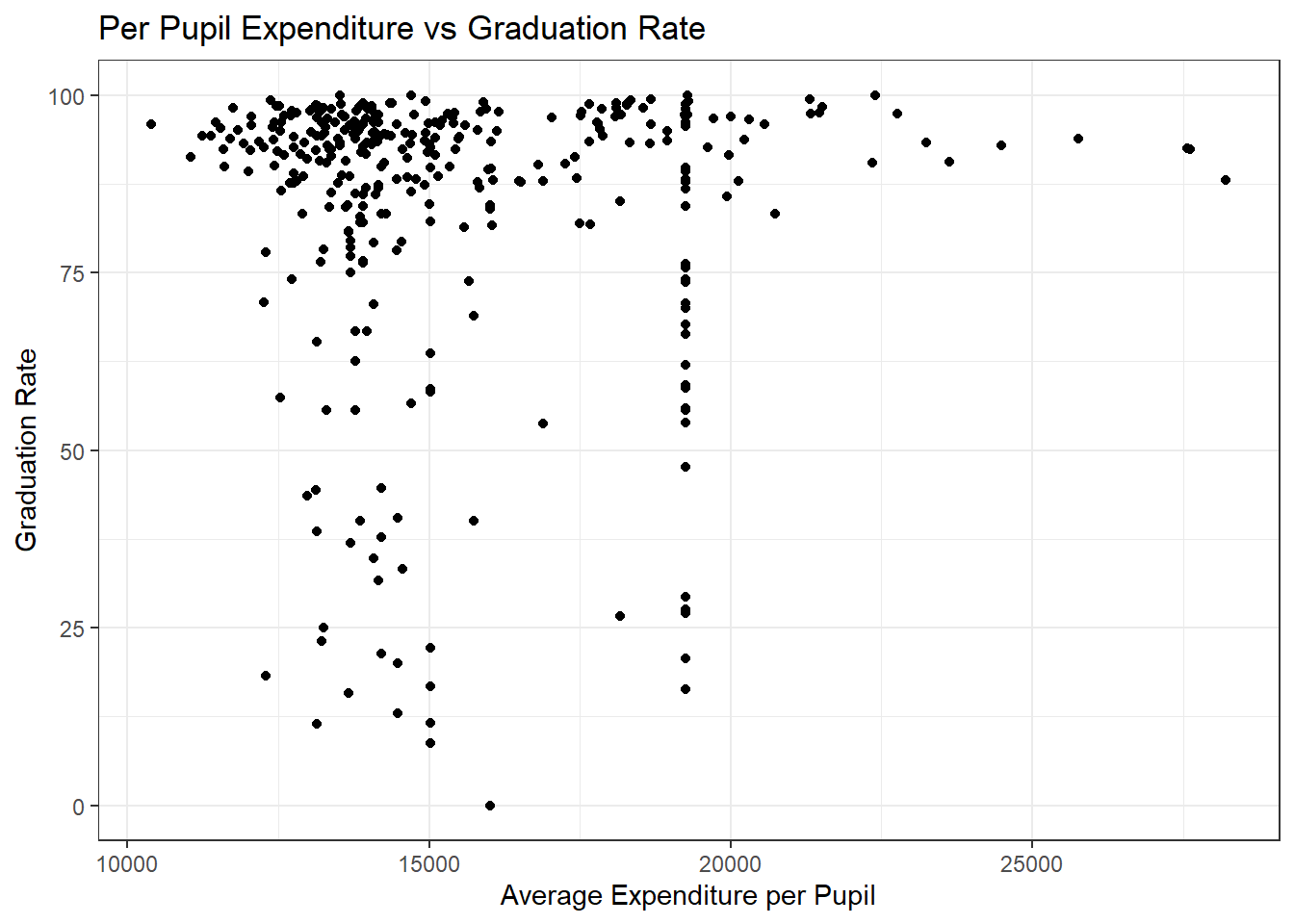
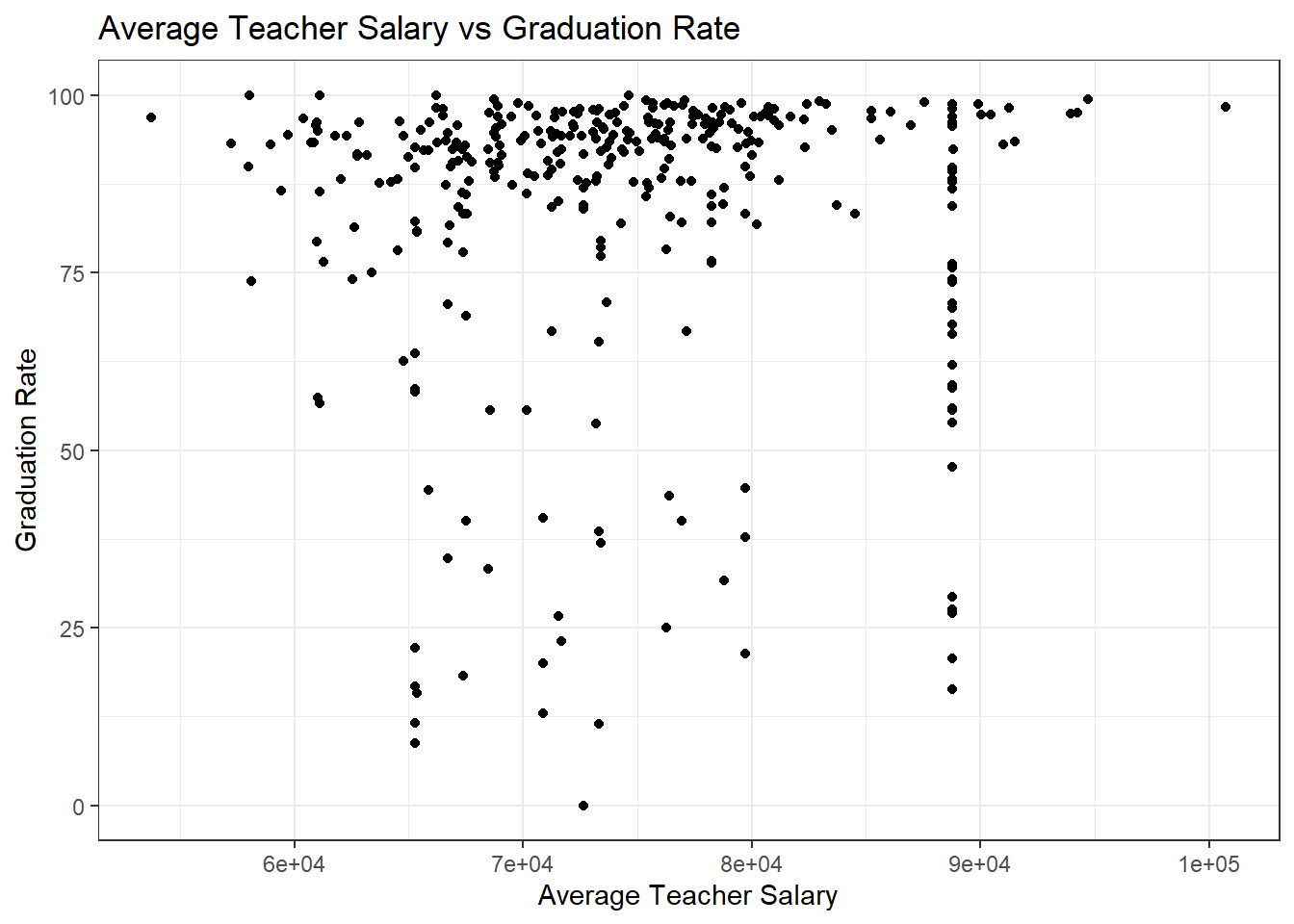
Something that sticks out to me from these two plots is the almost all of the schools with low graduation rates fall below a certain threshold, suggesting to me that while not all low income schools have low graduation rates, almost all schools with low graduation rates don’t pay teachers very highly or spend as much on each student.

Another thing to notice is that graduation rate does not increase continuously, as it is capped in the 95%+ range. This makes sense as you can only get so close to 100% graduation rate, but this calls to question whether the extra $10000 per student that some schools spend is worth the money, or if there is wasted spending which could be better allocated in lower income schools.

Another thing to note is the straight line with varying data that is present in both charts. This is due to average salary being reported by district and Boston Public Schools encompasses many schools which have varying results due to more socioeconomic factors than just salary or expenditure.

Test Scores

I think a good focus for my research will be looking into how salary and spending on students affects test scores. Below are two more scatter plots, similar to the ones we had above, for AP Test Scores vs salary and expenditures.

Code

hs <- mutate(hs, `Average AP Score` = (`AP_Score=1` + 2*`AP_Score=2` + 3*`AP_Score=3` + 4*`AP_Score=4` + 5*`AP_Score=5`)/`AP_Tests Taken`)

ggplot(hs, aes(x=`Average Salary`, y=`% Graduated`)) + geom_point()+
  theme_bw() +
  labs(title ="Average Teacher Salary vs AP Test Scores", y = "Average AP Test Score", x = "Average Teacher Salary")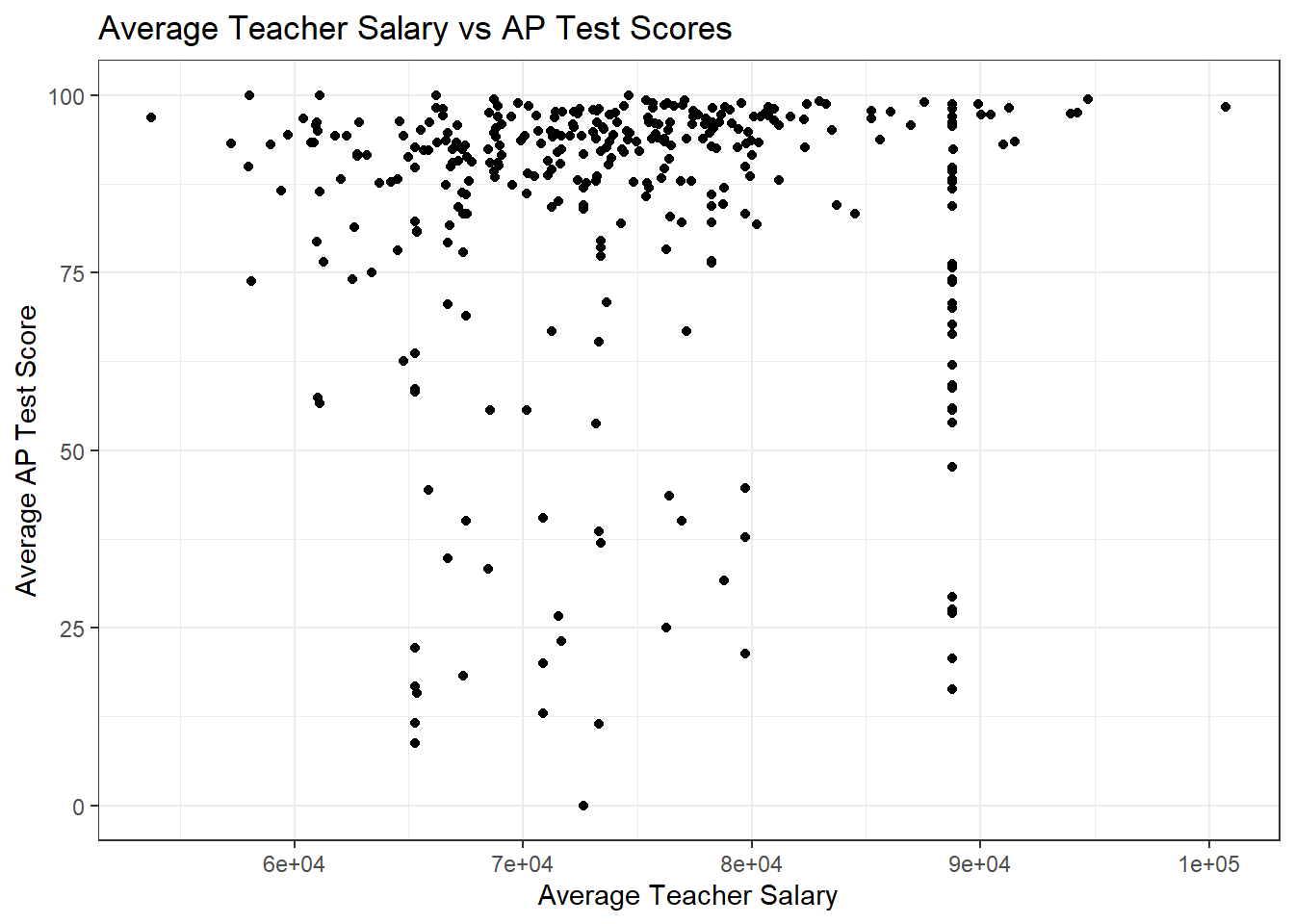

Above we once again see visually that many of the lowest scoring schools tend to collect in the same kind of range. We can investigate this further by looking at the mean SAT scores in different salary brackets.

Code

math <- aggregate(hs$ `Average SAT_Math`,list(hs$`Salary Bracket`),FUN=mean, na.rm=TRUE)
read <- aggregate(hs$`Average SAT_Reading`,list(hs$`Salary Bracket`),FUN=mean, na.rm=TRUE)
write <- aggregate(hs$`Average SAT_Writing`,list(hs$`Salary Bracket`),FUN=mean, na.rm=TRUE)

math

                    Group.1        x
1 Between $55000 and $60000 524.0000
2 Between $60000 and $65000 508.5385
3 Between $65000 and $70000 496.3898
4 Between $70000 and $75000 517.4722
5 Between $75000 and $80000 516.4412
6 Between $80000 and $85000 523.4091
7 Between $85000 and $90000 451.5714
8       Greater than $90000 595.5556
9          Less than $55000 500.0000

Code

read

                    Group.1        x
1 Between $55000 and $60000 526.5714
2 Between $60000 and $65000 504.4615
3 Between $65000 and $70000 491.8983
4 Between $70000 and $75000 510.2639
5 Between $75000 and $80000 501.4412
6 Between $80000 and $85000 514.7727
7 Between $85000 and $90000 425.4857
8       Greater than $90000 577.7778
9          Less than $55000 520.0000

Code

write

                    Group.1        x
1 Between $55000 and $60000 507.4286
2 Between $60000 and $65000 485.2692
3 Between $65000 and $70000 475.0508
4 Between $70000 and $75000 494.3889
5 Between $75000 and $80000 490.1471
6 Between $80000 and $85000 498.6818
7 Between $85000 and $90000 421.0571
8       Greater than $90000 572.0000
9          Less than $55000 504.0000

There doesn’t seem to be a perfect correlation, but this could be due to other factors, especially socioeconomic ones. The brackets are also not equal in size, as most districts pay teachers in the 65000 to 85000 range. Looking at those ranges alone, there does seem to be a general trend upward in SAT scores, with the exception of the 85000 district which contains Boston Public schools, which varies widely in scores due to a variety of socioeconomic factors that cannot be simplifed down to just teacher salary.

Visualization Limitations

The visualizations are fairly simple and bland, While they might be clear to understand, the takeaways might noe be very clear. The final paper could benefit from a wider variety of vsiaulizations, with some box plots and histograms. I also think the visualizations need to be more complex in order to make the conclusions easier to understand.

Some ideas I have include having plots for all 5 different AP scores, not just the average, and showing the number of AP test takers there are in each school, which is a function of investment in a school, since not all schools can afford to offer many AP courses.