DACSS 603 Final Project Pt 2

Setup

Code

library(tidyverse)

── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
✔ ggplot2 3.3.6      ✔ purrr   0.3.5 
✔ tibble  3.1.8      ✔ dplyr   1.0.10
✔ tidyr   1.2.1      ✔ stringr 1.4.1 
✔ readr   2.1.3      ✔ forcats 0.5.2 
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()

Code

library(readr)
library(scales)

Attaching package: 'scales'

The following object is masked from 'package:purrr':

    discard

The following object is masked from 'package:readr':

    col_factor

Code

library(ggplot2)

# Importing datasets

NYC_2019 <- read_csv("_data/2018-2019_School_Demographic_Snapshot.csv", col_types = cols(`Grade PK (Half Day & Full Day)` = col_skip(), `# Multiple Race Categories Not Represented` = col_skip(), `% Multiple Race Categories Not Represented` = col_skip()))

NYC_2019$`% Poverty` <- percent(NYC_2019$`% Poverty`, accuracy=0.1)

NYC_2021 <- read_csv("_data/2020-2021_Demographic_Snapshot_School.csv", col_types = cols(`Grade 3K+PK (Half Day & Full Day)` = col_skip(), `# Multi-Racial` = col_skip(), `% Multi-Racial` = col_skip(), `# Native American` = col_skip(), `% Native American` = col_skip(), `# Missing Race/Ethnicity Data` = col_skip(), `% Missing Race/Ethnicity Data` = col_skip()))

# In order to bind the data, I had to remove columns that were not present in the other spreadsheet: Grade PK or 3K, Native American, the different multi-racial categories, and Missing Data

school_data <- rbind(NYC_2019, NYC_2021)

# Renaming some columns

school_data$pct_white <- school_data$'% White'

# Making values coded as "above 95%" to equal 95% and "below 5%" to equal 5% for the purposes of this analysis

school_data$`% Poverty` <- recode(school_data$`% Poverty`, "Above 95%" = "95%", "Below 5%" = "5%")

# Re-coding variables as numeric

school_data$`% Poverty` <- sapply(school_data$`% Poverty`, function(x) gsub("%", "", x))

school_data$`% Poverty` <- as.numeric(school_data$`% Poverty`)

school_data$`Economic Need Index` <- as.numeric(school_data$`Economic Need Index`)

Warning: NAs introduced by coercion

Code

# Creating a new variable of post-Covid (1) and pre-Covid (0)

school_data$Post_Covid <- ifelse(school_data$Year == "2020-21", c("1"), c("0"))

Research Question

The research question I want to explore is whether child poverty has increased in schools that are predominantly made up of non-white students from the 2014-2015 school year to the 2020-2021 school year. I think this is extremely important to look at because of the pandemic’s impact on not only child learning but also families’ economic resources. According to the Columbia University Center on Poverty and Social Policy, “nearly a quarter of children ages 0-3 live in poverty and nearly half of the city’s young children live in lower-opportunity neighborhoods where the poverty rate is at least 20 percent” (“Poverty”). Unfortunately, research shows that poverty is disproportionately felt according to one’s race or ethnicity. In New York State, as of 2021, child poverty among children of color is almost 30%, with Black or African American children more than twice as likely to live in poverty than White, Non-Hispanic children (“New York State”, 2021). With this disproportionate level of economic need in children of color, it seems important to investigate if the poverty level within New York City schools that are predominately non-White has increased significantly compared to schools that are predominantly White. When searching the UMass Libraries databases and other sources, it was hard to find studies that used this data in this way. It is important to understand if there is increasing poverty levels within an already vulnerable group.

Hypothesis

I hypothesize that the poverty rate in NYC schools that are predominantly children of color will have increased more between pre- and post-Covid than the poverty rate in schools that are predominantly White. Since I have not found many previous studies on this, it is hard to know if this hypothesis was tested before. However, this data is fairly recent and also relates to the pandemic’s effects on economics, so I think it is still a significant contribution to test this hypothesis.

Descriptive Statistics

A description and summary of your data. How was your data collected by its original collectors? What are the important variables of interest for your research question? Use functions like glimpse() and summary() to present your data.

The data was collected by New York City and put on its Open Data source. The data covers NYC schools in the academic years 2014-2015 to 2020-2021. The important variables of interest included in the data are:

• Academic year, which I transformed into pre-Covid and post-Covid variables

• Number and percentage of Asisan, Black, Hispanic, and White students

• Number and percentage of students in poverty

• Economic need index, which is the average of students’ “Economic Need Values”

  • The Economic Need Index (ENI) estimates the percentage of students facing economic hardship

The other variables included are: DBN (district, borough, school number), school name, total enrollment, enrollment numbers for K-12, number and percentage of female and male students, number and percentage of students with disabilities, and number and percentage of English-Language Learner (ELL) students.

Code

glimpse(school_data)

Rows: 18,142
Columns: 38
$ DBN                            <chr> "01M015", "01M015", "01M015", "01M015",…
$ `School Name`                  <chr> "P.S. 015 Roberto Clemente", "P.S. 015 …
$ Year                           <chr> "2014-15", "2015-16", "2016-17", "2017-…
$ `Total Enrollment`             <dbl> 183, 176, 178, 190, 174, 270, 270, 271,…
$ `Grade K`                      <dbl> 27, 32, 28, 28, 20, 44, 47, 37, 34, 30,…
$ `Grade 1`                      <dbl> 47, 33, 33, 32, 33, 40, 43, 46, 38, 39,…
$ `Grade 2`                      <dbl> 31, 39, 27, 33, 30, 39, 41, 47, 42, 43,…
$ `Grade 3`                      <dbl> 19, 23, 31, 23, 30, 35, 43, 40, 46, 41,…
$ `Grade 4`                      <dbl> 17, 17, 24, 31, 20, 40, 35, 43, 42, 44,…
$ `Grade 5`                      <dbl> 24, 18, 18, 26, 28, 42, 40, 34, 42, 42,…
$ `Grade 6`                      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 7`                      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 8`                      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 9`                      <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 10`                     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 11`                     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `Grade 12`                     <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ `# Female`                     <dbl> 84, 83, 83, 99, 85, 132, 125, 127, 114,…
$ `% Female`                     <dbl> 0.459, 0.472, 0.466, 0.521, 0.489, 0.48…
$ `# Male`                       <dbl> 99, 93, 95, 91, 89, 138, 145, 144, 143,…
$ `% Male`                       <dbl> 0.541, 0.528, 0.534, 0.479, 0.511, 0.51…
$ `# Asian`                      <dbl> 8, 9, 14, 20, 24, 30, 27, 24, 23, 14, 2…
$ `% Asian`                      <dbl> 0.044, 0.051, 0.079, 0.105, 0.138, 0.11…
$ `# Black`                      <dbl> 65, 57, 51, 52, 48, 47, 55, 51, 49, 52,…
$ `% Black`                      <dbl> 0.355, 0.324, 0.287, 0.274, 0.276, 0.17…
$ `# Hispanic`                   <dbl> 107, 105, 105, 110, 95, 158, 169, 180, …
$ `% Hispanic`                   <dbl> 0.585, 0.597, 0.590, 0.579, 0.546, 0.58…
$ `# White`                      <dbl> 2, 2, 4, 6, 6, 27, 16, 15, 16, 18, 25, …
$ `% White`                      <dbl> 0.011, 0.011, 0.022, 0.032, 0.034, 0.10…
$ `# Students with Disabilities` <dbl> 64, 60, 51, 49, 38, 82, 82, 88, 90, 92,…
$ `% Students with Disabilities` <dbl> 0.350, 0.341, 0.287, 0.258, 0.218, 0.30…
$ `# English Language Learners`  <dbl> 17, 16, 12, 8, 8, 18, 13, 9, 8, 8, 120,…
$ `% English Language Learners`  <dbl> 0.093, 0.091, 0.067, 0.042, 0.046, 0.06…
$ `# Poverty`                    <chr> "169", "149", "152", "161", "145", "200…
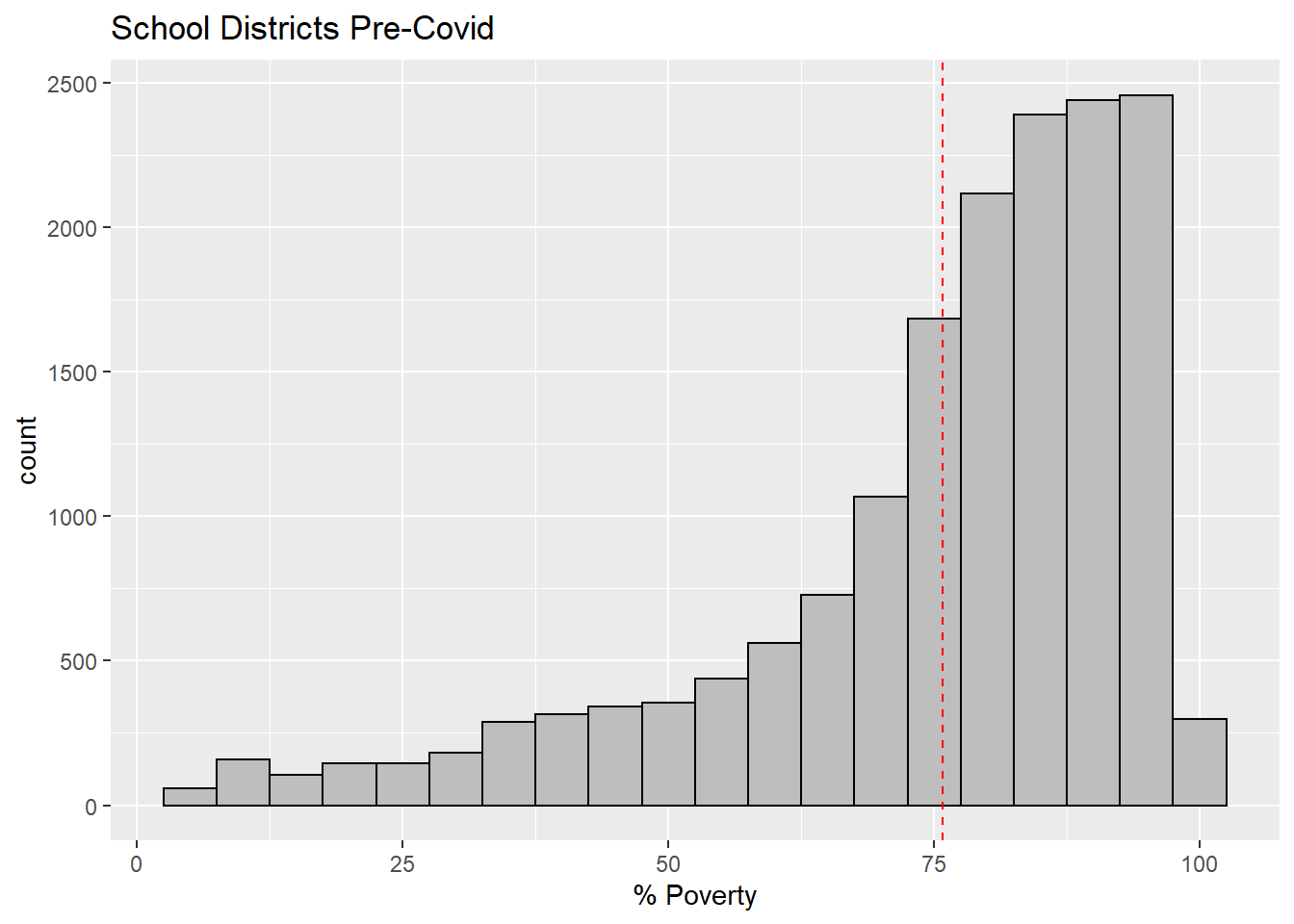
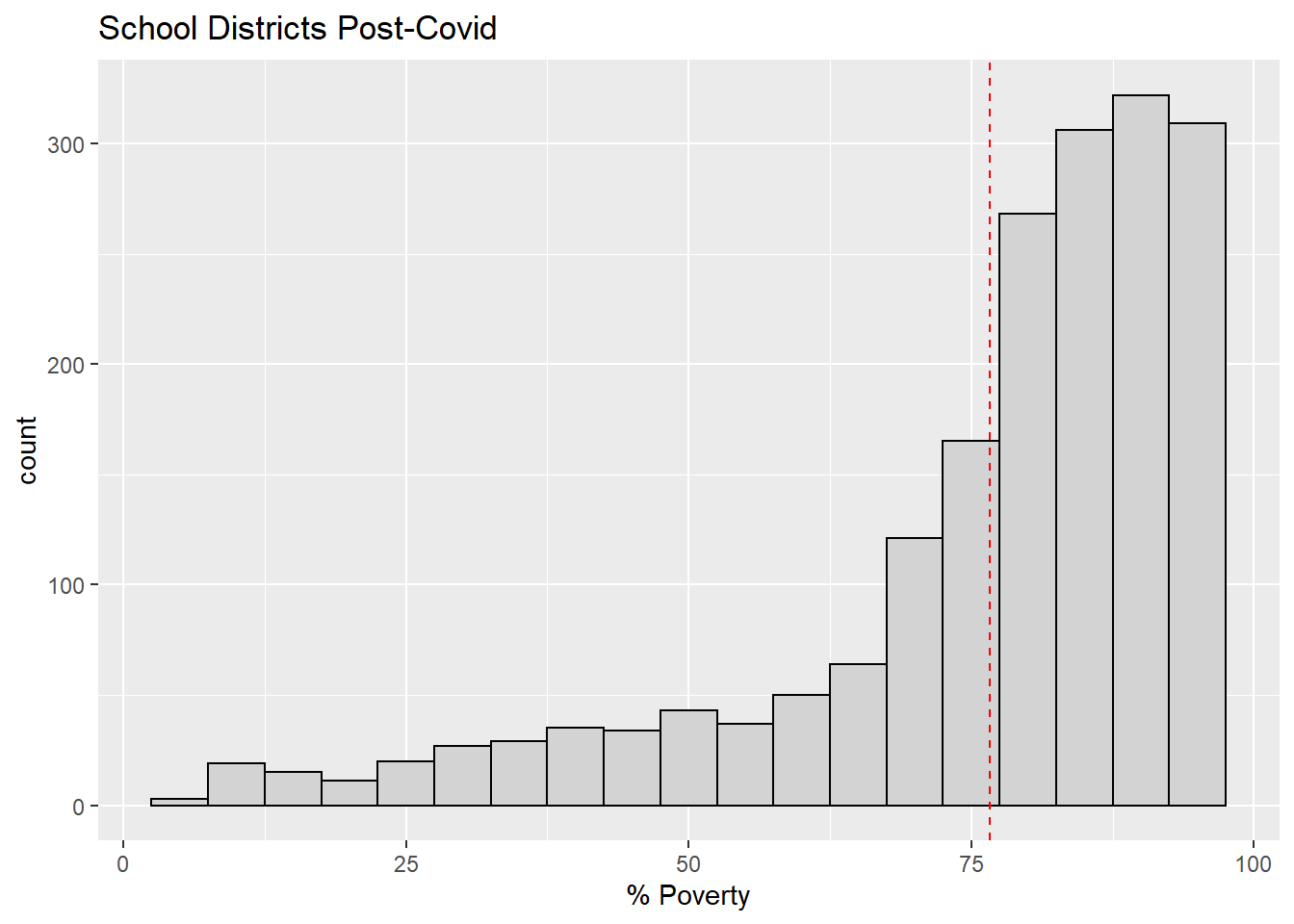
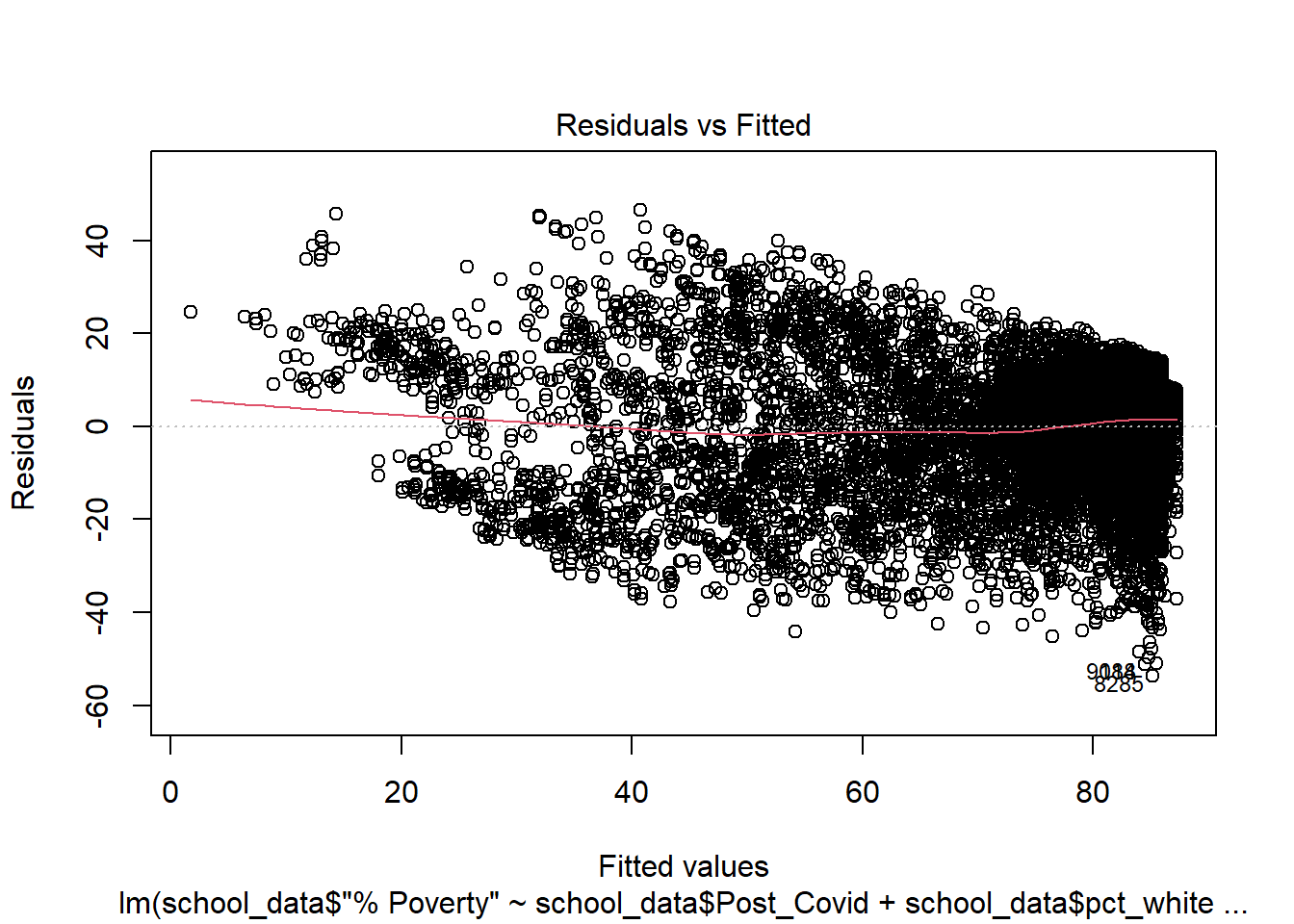
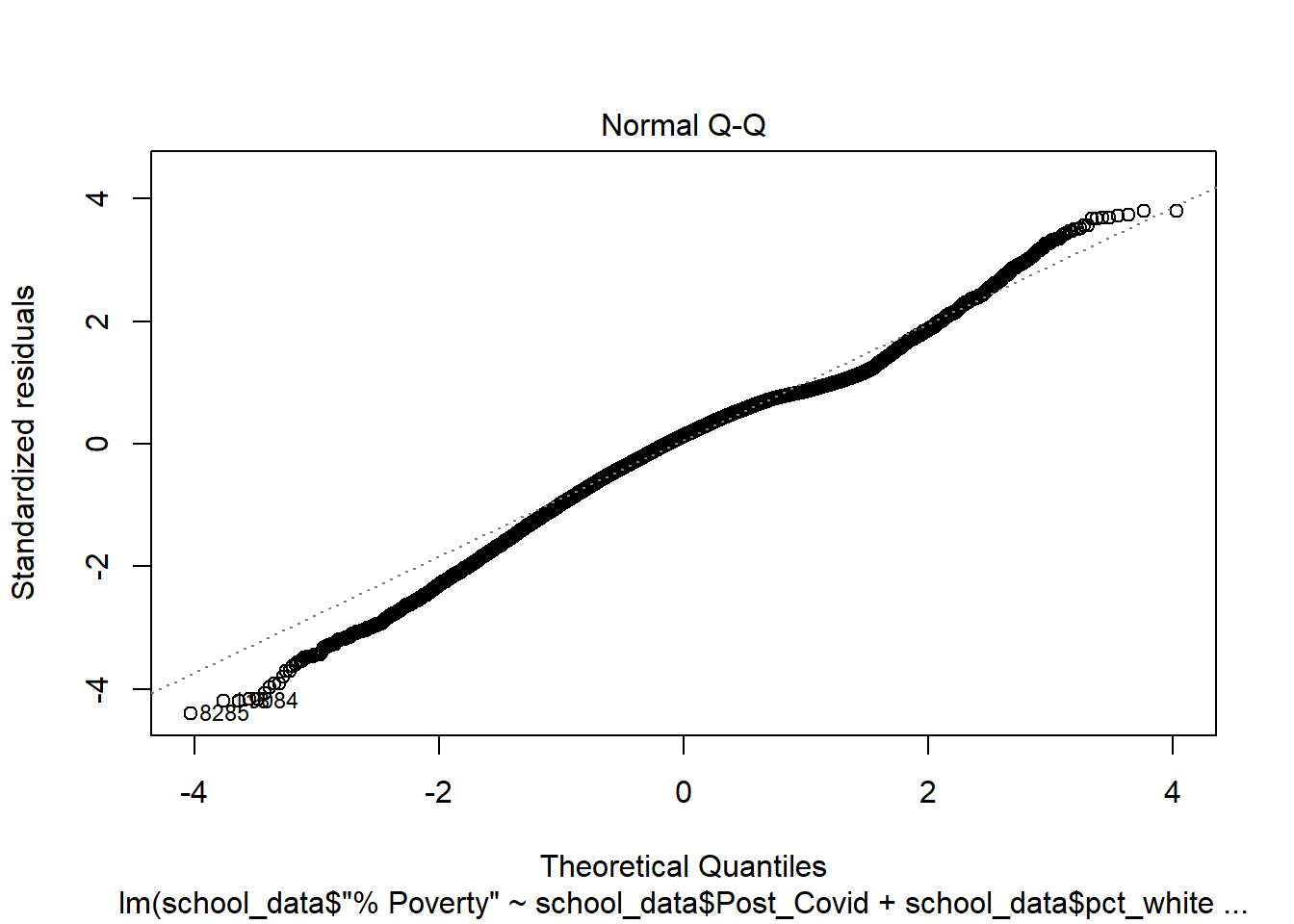
$ `% Poverty`                    <dbl> 92.3, 84.7, 85.4, 84.7, 83.3, 74.1, 80.…
$ `Economic Need Index`          <dbl> 0.930, 0.889, 0.882, 0.890, 0.880, 0.60…
$ pct_white                      <dbl> 0.011, 0.011, 0.022, 0.032, 0.034, 0.10…
$ Post_Covid                     <chr> "0", "0", "0", "0", "0", "0", "0", "0",…

Code

summary(school_data)

     DBN            School Name            Year           Total Enrollment
 Length:18142       Length:18142       Length:18142       Min.   :   7.0  
 Class :character   Class :character   Class :character   1st Qu.: 323.0  
 Mode  :character   Mode  :character   Mode  :character   Median : 477.0  
                                                          Mean   : 592.3  
                                                          3rd Qu.: 695.0  
                                                          Max.   :6040.0  
                                                                          
    Grade K          Grade 1          Grade 2          Grade 3      
 Min.   :  0.00   Min.   :  0.00   Min.   :  0.00   Min.   :  0.00  
 1st Qu.:  0.00   1st Qu.:  0.00   1st Qu.:  0.00   1st Qu.:  0.00  
 Median : 32.00   Median : 33.00   Median : 32.00   Median : 28.00  
 Mean   : 44.25   Mean   : 45.79   Mean   : 45.73   Mean   : 45.33  
 3rd Qu.: 78.00   3rd Qu.: 81.00   3rd Qu.: 82.00   3rd Qu.: 81.00  
 Max.   :393.00   Max.   :383.00   Max.   :349.00   Max.   :369.00  
                                                                    
    Grade 4         Grade 5          Grade 6          Grade 7      
 Min.   :  0.0   Min.   :  0.00   Min.   :  0.00   Min.   :  0.00  
 1st Qu.:  0.0   1st Qu.:  0.00   1st Qu.:  0.00   1st Qu.:  0.00  
 Median : 22.0   Median : 19.00   Median :  0.00   Median :  0.00  
 Mean   : 44.8   Mean   : 44.18   Mean   : 43.15   Mean   : 42.37  
 3rd Qu.: 80.0   3rd Qu.: 80.00   3rd Qu.: 64.00   3rd Qu.: 62.00  
 Max.   :376.0   Max.   :351.00   Max.   :771.00   Max.   :796.00  
                                                                   
    Grade 8          Grade 9           Grade 10         Grade 11      
 Min.   :  0.00   Min.   :   0.00   Min.   :   0.0   Min.   :   0.00  
 1st Qu.:  0.00   1st Qu.:   0.00   1st Qu.:   0.0   1st Qu.:   0.00  
 Median :  0.00   Median :   0.00   Median :   0.0   Median :   0.00  
 Mean   : 41.88   Mean   :  49.34   Mean   :  48.7   Mean   :  39.85  
 3rd Qu.: 60.00   3rd Qu.:  68.00   3rd Qu.:  69.0   3rd Qu.:  54.00  
 Max.   :784.00   Max.   :1555.00   Max.   :3832.0   Max.   :1529.00  
                                                                      
    Grade 12          # Female         % Female          # Male      
 Min.   :   0.00   Min.   :   0.0   Min.   :0.0000   Min.   :   0.0  
 1st Qu.:   0.00   1st Qu.: 146.0   1st Qu.:0.4620   1st Qu.: 163.0  
 Median :   0.00   Median : 232.0   Median :0.4880   Median : 248.0  
 Mean   :  39.58   Mean   : 287.4   Mean   :0.4827   Mean   : 304.9  
 3rd Qu.:  53.00   3rd Qu.: 347.0   3rd Qu.:0.5130   3rd Qu.: 364.0  
 Max.   :1566.00   Max.   :2405.0   Max.   :1.0000   Max.   :3635.0  
                                                                     
     % Male          # Asian           % Asian          # Black      
 Min.   :0.0000   Min.   :   0.00   Min.   :0.0000   Min.   :   0.0  
 1st Qu.:0.4870   1st Qu.:   5.00   1st Qu.:0.0130   1st Qu.:  42.0  
 Median :0.5120   Median :  17.00   Median :0.0400   Median : 105.0  
 Mean   :0.5173   Mean   :  95.38   Mean   :0.1136   Mean   : 154.1  
 3rd Qu.:0.5380   3rd Qu.:  79.00   3rd Qu.:0.1400   3rd Qu.: 198.0  
 Max.   :1.0000   Max.   :3671.00   Max.   :0.9470   Max.   :1493.0  
                                                                     
    % Black        # Hispanic     % Hispanic        # White       
 Min.   :0.000   Min.   :   1   Min.   :0.0060   Min.   :   0.00  
 1st Qu.:0.083   1st Qu.:  89   1st Qu.:0.1980   1st Qu.:   6.00  
 Median :0.251   Median : 180   Median :0.3990   Median :  15.00  
 Mean   :0.316   Mean   : 241   Mean   :0.4251   Mean   :  87.24  
 3rd Qu.:0.502   3rd Qu.: 313   3rd Qu.:0.6323   3rd Qu.:  78.00  
 Max.   :0.987   Max.   :2056   Max.   :1.0000   Max.   :3190.00  
                                                                  
    % White       # Students with Disabilities % Students with Disabilities
 Min.   :0.0000   Min.   :  0.0                Min.   :0.0000              
 1st Qu.:0.0140   1st Qu.: 66.0                1st Qu.:0.1570              
 Median :0.0330   Median : 98.0                Median :0.2030              
 Mean   :0.1205   Mean   :121.6                Mean   :0.2295              
 3rd Qu.:0.1440   3rd Qu.:146.0                3rd Qu.:0.2540              
 Max.   :0.9450   Max.   :925.0                Max.   :1.0000              
                                                                           
 # English Language Learners % English Language Learners  # Poverty        
 Min.   :   0.0              Min.   :0.0000              Length:18142      
 1st Qu.:  18.0              1st Qu.:0.0430              Class :character  
 Median :  43.0              Median :0.0950              Mode  :character  
 Mean   :  81.1              Mean   :0.1363                                
 3rd Qu.: 100.0              3rd Qu.:0.1800                                
 Max.   :1219.0              Max.   :1.0000                                
                                                                           
   % Poverty      Economic Need Index   pct_white       Post_Covid       
 Min.   :  2.90   Min.   :0.030       Min.   :0.0000   Length:18142      
 1st Qu.: 69.30   1st Qu.:0.579       1st Qu.:0.0140   Class :character  
 Median : 81.40   Median :0.743       Median :0.0330   Mode  :character  
 Mean   : 75.89   Mean   :0.691       Mean   :0.1205                     
 3rd Qu.: 89.90   3rd Qu.:0.846       3rd Qu.:0.1440                     
 Max.   :100.00   Max.   :0.998       Max.   :0.9450                     
                  NA's   :9169                                           

Code

# Note: the summary data for the enrollment numbers split by grade is somewhat off (especially minimums) because there is no variable listed for type of school (i.e., middle versus high school). So, for example, an elementary school would have an enrollment total of 0 for grade 12, which would show up as the minimum.

As we can see from this summary, the median percent of poverty in NYC schools (81.4%) is higher than the mean percent (75.89%), indicating that there may be low outliers with very low percentages of poverty. The same holds true for the Economic Need Index, with the mean (0.691) lower than the median (0.743). It is troubling, however, that both the mean and median percentages of poverty in NYC schools overall is more than three-fourths of the population.

Visualizations

Code

post_white <- filter(school_data, pct_white > 0.5 & Post_Covid == "1")
post_nonwhite <- filter(school_data, pct_white <= 0.5 & Post_Covid == "1")
pre_white <- filter(school_data, pct_white > 0.5 & Post_Covid == "0")
pre_nonwhite <- filter(school_data, pct_white <= 0.5 & Post_Covid == "0")
post <- filter(school_data, Post_Covid == "1")
pre <- filter(school_data, Post_Covid == "0")
white <- filter(school_data, pct_white > 0.5)
nonwhite <- filter(school_data, pct_white <= 0.5)

Code

boxplot(school_data$`% Poverty` ~ school_data$Post_Covid,
        xlab = "Pre-Covid (0) or Post-Covid (1)",
        ylab = "Percent of Students in Poverty")

From the box plot above, we can see that poverty levels between pre- and post-Covid did not change very dramatically for overall students. However, the maximum percentage of poverty did decrease from close to 100% to about 95%. Yet the median percentage level of poverty increased from pre- to post-Covid, though still remained under 90%. There are a large number of outliers below the minimum level of poverty, which is interesting–yet the minimum level of poverty increased between pre- and post-Covid.

Code

boxplot(white$`% Poverty` ~ white$Post_Covid,
        xlab = "Pre-Covid (0) or Post-Covid (1)",
        ylab = "Percent of Students in Majority White Districts in Poverty",
        cex.lab = 0.75)

The box plot showing majority white districts’ poverty levels pre- and post-Covid indicate that, while the median poverty level did not change dramatically, the maximum percentage and the third quartile percentage of poverty decreased between pre- and post-Covid. There was a high outlier pre-Covid, but this disappeared in the post-Covid box plot. The majority of observations for predominantly white schools fall in between about 15%-40% of students in poverty, for both pre- and post-Covid levels.

Code

boxplot(nonwhite$`% Poverty` ~ nonwhite$Post_Covid,
        xlab = "Pre-Covid (0) or Post-Covid (1)",
        ylab = "Percent of Students in Majority Non-White Districts in Poverty",
        cex.lab = 0.75)

The box plot for majority non-white districts’ poverty levels has a large number of outliers under the poverty level of 50%, similar to the plot for all school districts. The median level of poverty actually increased slightly between pre- and post-Covid years, along with the minimum level of poverty (both in the plot and in outliers). The maximum level of poverty, however, decreased more between these years. A majority of obersvations for both pre- and post-Covid are between 70%-90% of students in poverty for majority non-white districts.

Code

ggplot(school_data, aes(x=`% Poverty`)) +
  geom_histogram(binwidth = 5, color="black", fill="white") +
  geom_vline(aes(xintercept=mean(`% Poverty`)), color="red", linetype="dashed")

From the histogram above, we can see that the mean percentage of poverty for all NYC school districts is just above 75%. Most observations are above the mean, with very few school districts below 50% poverty levels. This is most likely why there were so many outliers in the box plots for all school districts and majority non-white school districts.

Code

ggplot(pre, aes(x=`% Poverty`)) +
  geom_histogram(binwidth = 5, color="black", fill="gray") +
  labs(title="School Districts Pre-Covid") +
  geom_vline(aes(xintercept=mean(`% Poverty`)), color="red", linetype="dashed")

Code

ggplot(post, aes(x=`% Poverty`)) +
  geom_histogram(binwidth = 5, color="black", fill="light gray") +
  labs(title="School Districts Post-Covid") +
  geom_vline(aes(xintercept=mean(`% Poverty`)), color="red", linetype="dashed")

The two different plots above show that a alightly larger share of districts post-Covid had poverty levels above the mean. The observations are very skewed to the left in all three plots, however.

Hypothesis Testing

Response variables: Percentage of students in poverty

Explanatory variables: Post- or pre-Covid, whether the school is majority or minority white

I’m including the interaction term of school demographics because I think that this does play a major role in how Covid effects were mitigated or compounded. Schools with more white students may have received more support during Covid, whether directly to the school or to the students themselves.

Null Hypothesis: The percentage of students in poverty is the same both pre- and post-Covid for both majority and minority white school districts.

Alternative Hypothesis: The percentage of students in poverty is higher post-Covid than pre-Covid, and this effect will be more drastic in minority white school districts than in majority white school districts.

Code

mean(post_white$'% Poverty') - mean(pre_white$'% Poverty')

[1] -0.9168508

Code

mean(post_nonwhite$'% Poverty') - mean(pre_nonwhite$'% Poverty')

[1] 0.4610488

Code

mean(post$'% Poverty') - mean(pre$'% Poverty')

[1] 0.8529465

Before conducting the hypothesis test, we already see that the differences between pre- and post-Covid poverty levels are very different for majority white and majorty nonwhite schools. Majority white schools actually had a decrease in poverty of 0.91% between pre-Covid and post-Covid school years. Yet majority nonwhite schools saw poverty increase between pre- and post-Covid by 0.46%. All school districts saw an overall 0.85% poverty increase in this time period. However, these numbers could be skewed since there is only one post-Covid year while there are a lot of years included in the data-set pre-Covid.

Code

# Hypothesis Test

model <- lm(school_data$'% Poverty' ~ school_data$Post_Covid + school_data$pct_white + school_data$Post_Covid * school_data$pct_white)
summary(model)

Call:
lm(formula = school_data$"% Poverty" ~ school_data$Post_Covid + 
    school_data$pct_white + school_data$Post_Covid * school_data$pct_white)

Residuals:
    Min      1Q  Median      3Q     Max 
-53.760  -7.076   1.633   8.534  46.497 

Coefficients:
                                              Estimate Std. Error  t value
(Intercept)                                    86.0034     0.1154  745.344
school_data$Post_Covid1                         1.2192     0.3620    3.368
school_data$pct_white                         -84.3586     0.5311 -158.838
school_data$Post_Covid1:school_data$pct_white  -6.1271     1.7540   -3.493
                                              Pr(>|t|)    
(Intercept)                                    < 2e-16 ***
school_data$Post_Covid1                       0.000757 ***
school_data$pct_white                          < 2e-16 ***
school_data$Post_Covid1:school_data$pct_white 0.000478 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.22 on 18138 degrees of freedom
Multiple R-squared:  0.6083,    Adjusted R-squared:  0.6082 
F-statistic:  9389 on 3 and 18138 DF,  p-value: < 2.2e-16

As seen from the results above, the p-values for all three coefficients are smaller than the significance level of a = 0.05. The results for the coefficient for the varaible Post-Covid indicate that there is statistically significant evidence to reject the null hypothesis, that the percentage of students in poverty is the same both pre- and post-Covid.

Model Comparisons

Code

model2 <- lm(school_data$'% Poverty' ~ school_data$Post_Covid + school_data$pct_white)
summary(model2)

Call:
lm(formula = school_data$"% Poverty" ~ school_data$Post_Covid + 
    school_data$pct_white)

Residuals:
    Min      1Q  Median      3Q     Max 
-53.822  -7.128   1.638   8.595  46.731 

Coefficients:
                        Estimate Std. Error  t value Pr(>|t|)    
(Intercept)              86.0713     0.1138  756.533   <2e-16 ***
school_data$Post_Covid1   0.5011     0.2980    1.681   0.0927 .  
school_data$pct_white   -84.9203     0.5063 -167.720   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.23 on 18139 degrees of freedom
Multiple R-squared:  0.608, Adjusted R-squared:  0.608 
F-statistic: 1.407e+04 on 2 and 18139 DF,  p-value: < 2.2e-16

In this second model without the interaction term, the Covid variable has a much higher p-value of 0.9, larger than the 0.05 significance level. This means that in this model, there is not significant evidence to reject the hypothesis that the percentage of students in poverty is the same both pre- and post-Covid. However, the p-value for the variable of the percentage of white students remains much smaller than the 0.05 significance level. There is still significant evidence in this model to reject the hypothesis that the percentage of students in poverty is the same for all percentages of white students in the school.

Though this model could still work, I think the first model with the interaction term would still be more accurate. As stated before, the effects of Covid on poverty levels would be mitigated by how much support students in these school districts had, and there is ample evidence that majority white areas receive much more support or are generally more affluent than majority nonwhite areas.

Diagnostics

Code

plot(model)

In the Residuals vs Fitted plot, the Residuals seem to be random around the linear line, indicating that the assumption of a linear relationship is reasonable.

In the Normal Q-Q plot, the points generally fall along the line, supporting the assumption of normal residuals.

The Scale-Location plot does show a slight downward trend, but is approximately horizontal for most of the graph. This means that standardized residuals could be changing because of the fitted values and it’s possible that there is not constant variance.

There are no points outside of the proper distance in the Residuals vs. Leverage plot, showing that there is no single influential observation.

References

New York State Child Poverty Facts. Schuyler Center for Analysis and Advocacy. (2021, February 18). Retrieved from https://scaany.org/wp-content/uploads/2021/02/NYS-Child-Poverty-Facts_Feb2021.pdf

Poverty in New York City. Columbia University Center on Poverty and Social Policy. (n.d.). Retrieved from https://www.povertycenter.columbia.edu/poverty-in-new-york-city#:~:text=Children%20and%20Families%20in%20New%20York%20City&text=Through%20surveys%2C%20we%20find%20that,is%20at%20least%2020%20percent.