PPP Loans: Party Affiliation and Loan Amount
PPP Loans: Party Affiliation and Loan Amount
Introduction
In the United States, the Paycheck Protection Program (PPP) was introduced as an emergency economic measure to prevent job loss during the 2020 Covid-19 pandemic. As a massive loan program with guaranteed forgiveness, some have criticized it for lax oversight. There have been many studies about the PPP focusing on its overall economic impact and the emergence of non-traditional, non-bank lenders. Less studied are political elements of the program.
My project leverages public-access data to compare federal PPP loan forgiveness amounts with political affiliation. Rather than using aggregate-level data like studies before, my analysis aimed to compare PPP recipients’ individual voter affiliation (e.g., who’s the owner of this business? Are they registered to vote in Florida? And to which party?) with their PPP loan outcome.
Targeting Florida, a state with liberal amounts of access to public voter registration and a closed primary (where a voter’s registration is better correlated with a person’s partisan identity), the individual-level version of this project was ultimately inconclusive due to data missing-not-at-random from Florida’s corporation/LLC database.
Following the discovery of the missing data, I approached the research question with county-level data from the 2020 presidential election, controlling for GDP and type of business.
Existing Work
Two interesting studies have been done about racial disparities re: access to PPP loans, with one finding that Black-owned businesses in Florida were 25% less likely to receive PPP funds (Chernenko & Scharfstein, 2022), and another measuring an even higher of a disparity (50%) among races but taking note of mitigating factors (e.g. access to “fintech” lending instead of traditional banks) (Atkins, Cook & Seamans).
I am not so much interested in the efficacy of the PPP or the racial make-up of PPP borrowers. But I am interested in their political affiliation, i.e. if they registered as Democratic or Republican. So, similarly to Chernenko & Scharfstein, I have used public-access data to cross-reference federal PPP data with state-level voter registration and corporation search data.
A relevant paper I found after I started looking at this data - “Buying the Vote? The Economics of Electoral Politics and Small-Business Loans” - does look at data from SBA and PPP loans and pit them against the hypothesis that “electoral considerations may have tilted the allocation of PPP funds toward firms in areas or industries that could have a significant impact on the results of the 2020 election” (Duchin & Hackney, 2021).
That particular study measured political ad spending and FEC filings as indicators of electoral considerations and used the Partisan Voting Index (PVI) from the Cook Political National Report to find which states were “battleground” or solid-R states. PPP lending outcomes were compared with electoral considerations to find if the SBA (under the Trump administration) preferred to give PPP loans to swing voters or members of the party “base” in anticipation of an upcoming general election.
Rather than aggregate-level state data, my original analysis attempted to compare individuals’ personal voter affiliation - if they are registered, and to which party - with their loan amount. Once I found that I could no longer proceed with the individual-level analysis due to missingness, I focused on using aggregate-level data to answer the research question.
Research Question
My research question is:
How does political affiliation affect PPP loan forgiveness status?
The data for PPP loans is current available on ProPublica, but not in a queryable way.
Fortunately, the underlying data has been made public by the SBA.
My hypotheses is:
Hypothesis 1 (H1): PPP loan forgiveness was given to registered Republicans more often than registered Democrats
Null Hypothesis (H0): There is no difference in loan forgiveness given to registered Democrats vs registered Republicans.
In some ways this is similar to Duchin & Hackney, but this benefits from a narrower look at who actually received PPP stimulus rather than eventual outcomes on the state level.
Clearly a few effects that would need to be controlled for. Loan forgiveness is likely affected by GDP per county and the industry of the loan recipient (e.g. aerospace, arts & crafts, etc…)
Ideally, I would have focused on my home state of Massachusetts. Although voter registration data is available for personal use in MA, you can’t download it all in one .csv, and scraping the Commonwealth’s website is not allowed.
Seeking an alternative, I noticed that the National Conference of State Legislatures keeps track of which states have full voter registration data for download. I selected Florida because:
PPP data is available for the state,
Florida’s corporation search database is downloadable (with some limitations),
Florida’s voter registration information is available to the public (which is surprisingly rare).
Florida is considered a ‘swing state’ or ‘battleground state’ - at least, it was in 2020.
Florida has a closed primary, which means that voter registration will be more indicative of true political affiliation.
This single document contains both individual-level and aggregate-level analysis, with all the data import, tidying, and analysis that comes with each.
For that reason, it’s a long document. I suggest skipping directly to the section titled “Another way: Aggregate-level data” to get to the most meaningful part of the project.
Reading, joining, and tidying individual-level data
PPP Data
Importing the data of the actual PPP loans is straightforward. ppp_1 and ppp_2 contain only the PPP loans below $150k - higher amounts are contained in ppp_3, a smaller spreadsheet that covers all 50 states.
```{r}
ppp_1 <- read_csv("_data/public_up_to_150k_3_220930.csv")
ppp_2 <- read_csv("_data/public_up_to_150k_4_220930.csv")
ppp_3 <- read_csv("_data/public_150k_plus_220930.csv")
```Helpfully, all files have the same columns.
PPP Data Dictionary
I have “double bracketed” many code chunks because the original data is too large to store in GitHub or on Google Drive. The output is read-in from .csvs instead.
This is a simple way to avoid loading massive, >1gb files.
The original source data is available at links in the Sources section. The full folder of dependencies is available upon request and can be easily reproduced by running the code contained.
To help understand which fields mean what, the SBA provides a PPP “Data Dictionary” with an explanation of columns [scroll right to see explanation]:
Code
ppp_data_dictionary <- read_excel("_data/ppp-data-dictionary.xlsx")
ppp_data_dictionaryHere, I filtered out other states and sampled down PPP data to just 10k rows for analysis:
Code
#ppp_all <- rbind(ppp_1, ppp_2, ppp_3)
#ppp_florida <- ppp_all %>% filter(BorrowerState == "FL")
#ppp_florida_sampled_10k <- ppp_florida %>% sample_n(10000)
#write_csv(ppp_florida_sampled_10k, "_data/ppp_florida_sampled_10k.csv")
#For the purposes of Github, I only read in the resultant CSV:
ppp_florida <- read_csv("_data/ppp_florida_sampled_10k.csv", show_col_types = FALSE)
ppp_floridaLLCs, Corporations
Visually, you may notice that businesses and LLCs make up many of the loan recipients.
To create a “crosswalk” between PPP data and voter registration data, it is necessary to look up corporation filing data on Florida’s FTP portal. Unfortunately, that data comes in thousands of separate files and is very messy. There aren’t even delimiters - this was “fixed-width” ASCII data.
Parsing Florida’s business data
The data comes thousands of individual files and surpasses 20GB. It is available here.
Corporations: pre-2010
Data from before 2010 is downloadable in a .dat extension.
```{r}
#| warning: false
setwd("_data\\florida_corps_all\\2010_prior")
#Get all .dat files and add to vector
fileNames <- Sys.glob("*.dat")
#Using a 'known-good' file as a position key:
fixed_positions <- fwf_empty(file = "081508c.dat")
#Custom insertion for corporation name
fixed_positions$begin <- append(fixed_positions$begin, 12, after = 1)
fixed_positions$end <- append(fixed_positions$end, 11, after = 0)
#Custom insertion for removing first character from registered agent address
fixed_positions$begin <- append(fixed_positions$begin, 317, after = 10)
fixed_positions$end <- append(fixed_positions$end, 316, after = 9)
interest_columns <- c('X2', 'X3', 'X4', 'X6', 'X9', 'X11', 'X12')
output_file <- "florida_corps_pre2010.csv"
for (fileName in fileNames) {
df <- read_fwf(file = fileName,
col_positions = fixed_positions,
locale = readr::locale(encoding = "latin1"),
show_col_types = FALSE)
#Remove completely empty rows
df <- filter(df, rowSums(is.na(df)) != ncol(df))
df <- df %>% select(interest_columns)
#Append to .csv in working directory
write.table(df,
output_file,
append = TRUE,
sep = ",",
row.names = FALSE,
col.names = FALSE)
}
``````{r}
#| warning: false
florida_corps_pre_2010 <- read_csv("_data/florida_corps_pre2010.csv", col_names = FALSE, show_col_types = FALSE)
#Completeness:
nrow(problems(florida_corps_pre_2010))
nrow(florida_corps_pre_2010)/ (nrow(florida_corps_pre_2010) + nrow(problems(florida_corps_pre_2010)))
#Result:
#[1] 0.9996532
``````{r}
colnames(florida_corps_pre_2010) <- c("corp_name","corp_type","corp_address","corp_city","corp_reg_agent","corp_reg_agent_address","corp_reg_agent_city")
florida_corps_pre_2010
```Corporations: post-2010
Post-2011 data has similar fixed-width properties and can be interpreted with different interest_columns and custom insertions. The method below gives a 92% savings in disk usage (6.28gb -> ~600mb) and brings everything into a tidy .csv with 4.6 million rows.
```{r}
#| warning: false
setwd("_data\\florida_corps_all\\20110103c")
#Get all .dat files and add to vector
fileNames <- Sys.glob("*.txt")
#Using a 'known-good' file as a position key:
fixed_positions <- fwf_empty(file = "20220103c.txt")
#Custom insertion for corporation name
fixed_positions$begin <- append(fixed_positions$begin, 12, after = 1)
fixed_positions$end <- append(fixed_positions$end, 11, after = 0)
#Custom insertion for removing first character from registered agent address
fixed_positions$begin <- append(fixed_positions$begin, 587, after = 25)
fixed_positions$end <- append(fixed_positions$end, 586, after = 24)
interest_columns <- c('X2', 'X4', 'X5', 'X11', 'X23', 'X26', 'X27')
output_file <- "florida_corps_post2010.csv"
for (fileName in fileNames) {
df <- read_fwf(file = fileName,
col_positions = fixed_positions,
locale = readr::locale(encoding = "latin1"),
show_col_types = FALSE)
#Remove completely empty rows
df <- filter(df, rowSums(is.na(df)) != ncol(df))
df <- df %>% select(interest_columns)
#Append to .csv in working directory
write.table(df,
output_file,
append = TRUE,
sep = ",",
row.names = FALSE,
col.names = FALSE)
}
``````{r}
#| warning: false
florida_corps_post_2010 <- read_csv("_data/florida_corps_post2010.csv", col_names = FALSE, show_col_types = FALSE)
#Completeness:
nrow(problems(florida_corps_post_2010))
nrow(florida_corps_post_2010)/ (nrow(florida_corps_post_2010) + nrow(problems(florida_corps_post_2010)))
#Result:
#[1] 0.9997638
``````{r}
colnames(florida_corps_post_2010) <- c("corp_name","corp_type","corp_address","corp_city","corp_reg_agent","corp_reg_agent_address","corp_reg_agent_city")
florida_corps_post_2010
```‘Aggregate’ corporation data
Finally, there is “aggregate” corporation data, which contains agent names but only references the corporation’s unique ID number. I do not find it very useful for our analysis, but I will include it in this file in case it is helpful later. There are 10 files in total; this is just one for representation:
```{r}
setwd("_data\\florida_corps_all\\corprindata")
#Using a 'known-good' file as a position key:
corps_fixed_positions <- fwf_empty(file = "corprindata0.txt")
corps_agg <- read_fwf(file = "corprindata0.txt",
#col_positions = corps_fixed_positions,
#locale = readr::locale(encoding = "latin1"))
#Remove trailing digits on zip code
corps_agg$X2 <- substr(corps_agg$X2,2,200L)
corps_agg
```Fictitious names
“Fictitious names” are records of people with ‘Doing Business As’ (DBA) businesses and trademarks. The data would not be complete without it.
Fictitious names pre-2011
```{r}
#| warning: false
setwd("_data\\florida_fic_name_db\\2011_prior")
#Get all .dat files and add to vector
fileNames <- Sys.glob("*.dat")
#Using a 'known-good' file as a position key:
fixed_positions <- fwf_empty(file = "010109f.dat")
#Custom insertion for corporation name
fixed_positions$begin <- append(fixed_positions$begin, 12, after = 1)
fixed_positions$end <- append(fixed_positions$end, 11, after = 0)
#Custom insertion for county
fixed_positions$begin <- append(fixed_positions$begin, 213, after = 3)
fixed_positions$end <- append(fixed_positions$end, 212, after = 2)
#Custom insertion for registered agent name
fixed_positions$begin <- append(fixed_positions$begin, 400, after = 12)
fixed_positions$end <- append(fixed_positions$end, 420, after = 11)
#Custom insertion for registered agent address
fixed_positions$begin <- append(fixed_positions$begin, 456, after = 15)
fixed_positions$end <- append(fixed_positions$end, 455, after = 14)
interest_columns <- c("X2", "X3", "X4", "X8", "X9", "X13", "X16", "X17")
output_file <- "florida_ficnames_pre2011.csv"
for (fileName in fileNames) {
df <- read_fwf(file = fileName,
col_positions = fixed_positions,
locale = readr::locale(encoding = "latin1"),
show_col_types = FALSE)
#Remove rows that are all NAs
df <- filter(df, rowSums(is.na(df)) != ncol(df))
#Select certain columns for disk space reasons
df <- df %>% select(interest_columns)
#Append to .csv in working directory
write.table(df,
output_file,
append = TRUE,
sep = ",",
row.names = FALSE,
col.names = FALSE)
}
``````{r}
#| warning: false
florida_ficnames_pre_2011 <- read_csv("_data/florida_ficnames_pre2011.csv", col_names = FALSE, show_col_types = FALSE)
#Completeness:
nrow(problems(florida_ficnames_pre_2011))
nrow(florida_ficnames_pre_2011)/ (nrow(florida_ficnames_pre_2011) + nrow(problems(florida_ficnames_pre_2011)))
#Result:
#[1] 0.999592
``````{r}
colnames(florida_ficnames_pre_2011) <- c("ficname_companyname","ficname_county","ficname_address","ficname_city","ficname_zip","ficname_reg_agent","ficname_reg_agent_address","ficname_reg_agent_city","ficname_reg_agent_zip")
```Fictitious names post-2011
```{r}
#| warning: false
setwd("_data\\florida_fic_name_db")
#Get all .dat files and add to vector
fileNames <- Sys.glob("*.txt")
#Using a 'known-good' file as a position key:
#.dat and .txt are interchangeable as 'key' files in this instance
fixed_positions <- fwf_empty(file = "010109f.dat")
#Custom insertion for corporation name
fixed_positions$begin <- append(fixed_positions$begin, 12, after = 1)
fixed_positions$end <- append(fixed_positions$end, 11, after = 0)
#Custom insertion for county
fixed_positions$begin <- append(fixed_positions$begin, 213, after = 3)
fixed_positions$end <- append(fixed_positions$end, 212, after = 2)
#Custom insertion for registered agent name
fixed_positions$begin <- append(fixed_positions$begin, 400, after = 12)
fixed_positions$end <- append(fixed_positions$end, 420, after = 11)
#Custom insertion for registered agent address
fixed_positions$begin <- append(fixed_positions$begin, 456, after = 15)
fixed_positions$end <- append(fixed_positions$end, 455, after = 14)
interest_columns <- c("X2", "X3", "X4", "X8", "X9", "X13", "X16", "X17")
output_file <- "florida_ficnames_post2011.csv"
for (fileName in fileNames) {
df <- read_fwf(file = fileName,
col_positions = fixed_positions,
locale = readr::locale(encoding = "latin1"),
show_col_types = FALSE)
#Remove rows that are all NAs
df <- filter(df, rowSums(is.na(df)) != ncol(df))
#Select certain columns for disk space reasons
df <- df %>% select(interest_columns)
#Append to .csv in working directory
write.table(df,
output_file,
append = TRUE,
sep = ",",
row.names = FALSE,
col.names = FALSE)
}
``````{r}
#| warning: false
florida_ficnames_post_2011 <- read_csv("_data/florida_ficnames_post2011.csv", col_names = FALSE, show_col_types = FALSE)
#Completeness:
nrow(problems(florida_ficnames_post_2011))
nrow(florida_ficnames_post_2011)/ (nrow(florida_ficnames_post_2011) + nrow(problems(florida_ficnames_post_2011)))
#Result
#[1] 0.9996022
``````{r}
colnames(florida_ficnames_post_2011) <- c("ficname_companyname","ficname_county","ficname_address","ficname_city","ficname_zip","ficname_reg_agent","ficname_reg_agent_address","ficname_reg_agent_city","ficname_reg_agent_zip")
florida_ficnames_post_2011
```Binding corporations and “fictitious names”
Here, the many dataframes were brought down to one: florida_businesses.
```{r}
#| output: false
#| warning: false
#Bind dataframes
florida_corps_all <- rbind(florida_corps_pre_2010, florida_corps_post_2010)
florida_ficnames_all <- rbind(florida_ficnames_pre_2011, florida_ficnames_post_2011)
#Select columns of interest
florida_corps_selection <- florida_corps_all %>% select(corp_name, corp_reg_agent, corp_reg_agent_address, corp_reg_agent_city)
florida_ficnames_selection <- florida_ficnames_all %>% select(ficname_companyname, ficname_reg_agent, ficname_reg_agent_address, ficname_reg_agent_city)
colnames(florida_corps_selection) <- c("business_name", "business_agent", "business_agent_address", "business_agent_city")
colnames(florida_ficnames_selection) <- c("business_name", "business_agent", "business_agent_address", "business_agent_city")
#Create one dataframe with all business entities.
florida_businesses <- rbind(florida_corps_selection, florida_ficnames_selection)
```Another (necessary) check for completeness.
It’s prudent to check that we are not leaving out any data. Remember that we 1.) looped through .dat and .txt files to transform and write to several .csv files, then 2.) read those .csv files back into R memory. The code chunks above checked to see if anything was missed after the read_csv() operations - mostly, we saw 99.9% accuracy.
However, we still need compare the number of rows of the original source .dat and .txt files with our dataframe output (using nrow()). The results will be inclusive of the errors found in the chunks above.
We expect the number of rows in the original native format to be the same as the number of rows in the dataframes they eventually were went into.
```{r}
#| warning: false
# Pre-2011 fictional names
setwd("C:\\Users\\stevenoneill\\Downloads\\florida_fic_name_db\\2011_prior")
filenames <- dir(pattern = "[.]dat$")
df <- sapply(filenames, function(x) length(count.fields(x, sep = "\1")))
names(df) <- NULL
print(sum(df))
nrow(florida_ficnames_pre_2011)
nrow(florida_ficnames_pre_2011) / sum(df)
# Post-2011 fictional names
setwd("C:\\Users\\stevenoneill\\Downloads\\florida_fic_name_db")
filenames <- dir(pattern = "[.]txt$")
df2 <- sapply(filenames, function(x) length(count.fields(x, sep = "\1")))
names(df2) <- NULL
print(sum(df2))
nrow(florida_ficnames_post_2011)
nrow(florida_ficnames_post_2011) / (sum(df2))
# Pre-2011 corporations
setwd("C:\\Users\\stevenoneill\\Downloads\\florida_corps_all\\2010_prior")
filenames <- dir(pattern = "[.]dat$")
df3 <- sapply(filenames, function(x) length(count.fields(x, sep = "\1")))
names(df3) <- NULL
print(sum(df3))
nrow(florida_corps_pre_2010)
nrow(florida_corps_pre_2010) / (sum(df3))
# Post-2011 corporations
setwd("C:\\Users\\stevenoneill\\Downloads\\florida_corps_all\\20110103c")
filenames <- dir(pattern = "[.]txt$")
df4 <- sapply(filenames, function(x) length(count.fields(x, sep = "\1")))
names(df4) <- NULL
print(sum(df4))
nrow(florida_corps_post_2010)
nrow(florida_corps_post_2010) / sum(df4)
```Strangely, the dataframe florida_corps_post_2010 actually has a few more rows than the original source data. This could be due to the company names containing the character sequence “\1”, which is meant to represent a new line in the syntax of R’s sep.
Either way, this is not too much of a concern. The final product, florida_businesses, simply has to serve as a look-up table. We will not be doing any regressions or analysis of the dataframe florida_businesses itself.
Duplicates
Are there any duplicates in here? It would be hard to tell by scrolling the 6.8 million rows (if my computer even let me do that.)
Instead, this code lets me see the percentage of rows that are totally unique - 99.7%. This is a sign that the data is accurate (although it may not be complete).
```{r}
unique_businesses <- florida_businesses %>% unique()
# 6,825,879 rows
nrow(unique_businesses) / nrow(florida_businesses)
#Result:
#[1] 0.9974421
```Simplifying business names for joining
I found that removing periods, commas, and apostrophes could make our next steps more accurate. I do want to keep ampersands and other characters, though.
```{r}
#Separated for the sake of not having a single complicated regex expression:
florida_businesses <- florida_businesses %>% mutate(business_name = str_remove_all(business_name, ","))
florida_businesses <- florida_businesses %>% mutate(business_name = str_remove_all(business_name, "\\."))
florida_businesses <- florida_businesses %>% mutate(business_name = str_remove_all(business_name, "\\'"))
```Obviously the same treatment should be given to the PPP data for which it will be joined to:
```{r}
ppp_florida <- ppp_florida %>% mutate(BorrowerName = str_remove_all(BorrowerName, ","))
ppp_florida <- ppp_florida %>% mutate(BorrowerName = str_remove_all(BorrowerName, "\\."))
ppp_florida <- ppp_florida %>% mutate(BorrowerName = str_remove_all(BorrowerName, "\\'"))
```Pre-formatting registered agent names for comparison
The “registered agents” found in florida_businesses, - usually, the owners of the companies - are characteristically formatted as an individual’s last name followed by a first name, separated by at least two (but sometimes 10 or more) whitespace characters, like this:
Code
GOODWIN DAVID SNot parsing these during the initial data read-in was an intentional choice to maintain the integrity of the data.
Now is the time to give these registered agent names the appropriate attention, resulting in new columns called business_agent_firstname, business_agent_lastname, and business_agent_initial.
```{r}
florida_businesses <- florida_businesses %>%
mutate(business_agent_firstname = str_trim(str_extract(business_agent, '[[:space:]]{2}(.*)'))) %>%
mutate(business_agent_lastname = str_trim(str_extract(business_agent, '(.*?)[[:space:]]{2}'))) %>%
mutate(business_agent_initial = str_trim(str_extract(business_agent_firstname, '[[:space:]]{2}(.*)'))) %>%
mutate(business_agent_firstname = str_remove(business_agent_firstname, '[[:space:]]{2}(.*)'))
```A word on registered agent services
At least 1.4 million out of 5.4 million corporations (25%) in our data use a registered agent service to protect their privacy and keep the company on track with filings. A registered agent service allows any LLC from out-of-state be incorporated in the state, since a registered agent must have legal residence in the state where the business is formed. Because registered agent services are basically required for any business that is headquartered in another state, we need to keep in mind that as long as we are using individual-level data, our final analysis will exclude companies which are founded in other states, or use registered agent services for any other reason.
There is no specific way to diagnose how this will affect our outcomes. “[A] lawyer, spouse or other relative, friend, or trusted person can serve as registered agent”, according to Nolo.com. Considering this, the assumption that the registered agent of a business is always the owner has perhaps been naive. A large company may designate its head accountant, for example, as the registered agent to manage the everyday business of taxes and filings. We also see the suffix “Esq.” appended to many of the registered agents’ names, meaning lawyers are probably standing in as registered agents using their own likenesses.
Businesses which use registered agent services will be excluded from the voter registration ‘join’ - there is unfortunately no way around it. Therefore, we should acknowledge that overall, businesses with a certain degree of sophistication will probably be missing from our analysis.
Joining PPP Data and Business Data
With all data currently available, here a the fairly simple join operation that merges Florida business records and our sample of 10k Floridian PPP loans. I am joining on the full company name, which is typically respected in the business world due to trademark norms (I didn’t see duplicates during exploratory data analysis).
```{r}
ppp_businesses_joined <- ppp_florida %>% drop_na(BorrowerName) %>% inner_join(florida_businesses, by = c("BorrowerName" = "business_name"), keep=TRUE, na_matches = c("na", "never")) %>% select("BorrowerName","business_name","business_agent","business_agent_firstname","business_agent_initial","business_agent_lastname","business_agent_address","BusinessType","JobsReported","NAICSCode","ProjectCountyName","BorrowerCity","Gender","Veteran","ForgivenessAmount", "Term") %>% distinct(BorrowerName, .keep_all = TRUE)
```Here is the file after it has been joined. I am reading it in from a CSV for the purposes of publishing to GitHub.
Code
ppp_businesses_joined <- read_csv( "_data/ppp_businesses_joined.csv", show_col_types = FALSE)
ppp_businesses_joined2,389 rows out of 10,000 were returned - that’s only 24% of what should be expected. Remember that we are matching our sample of Florida PPP recipients with our ‘edition’ of the Florida corporation database (which is not necessarily complete). In the join above, we would expect closer to 10k, which would be full coverage.
Let’s examine what was included in our inner_join and see if it skews a certain way:
Code
print(summarytools::dfSummary(ppp_businesses_joined$BusinessType,
varnumbers = FALSE,
plain.ascii = FALSE,
style = "grid",
graph.magnif = 0.70,
valid.col = FALSE),
method = 'render',
table.classes = 'table-condensed')Yes, as seen here, it is very skewed - this matched data favors LLCs (44.4% in sample vs population percentage of 18.10%) and corporations (33.7% in sample vs 21.5% out of the population). It also tends to exclude sole proprietors (5.1% in sample vs population of 24.5%).
I also used an anti_join to see what’s left out:
Code
#ppp_businesses_anti_joined <- ppp_florida %>% drop_na(BorrowerName) %>% anti_join(florida_businesses, by = c("BorrowerName" = "business_name"), keep=TRUE, na_matches = c("na", "never")) %>% distinct(BorrowerName, .keep_all = TRUE)
ppp_businesses_anti_joined <- read_csv("_data/ppp_businesses_anti_joined.csv", show_col_types = FALSE)
print(summarytools::dfSummary(ppp_businesses_anti_joined$BusinessType,
varnumbers = FALSE,
plain.ascii = FALSE,
style = "grid",
graph.magnif = 0.70,
valid.col = FALSE),
method = 'render',
table.classes = 'table-condensed')In the anti-joined results, many of the unmatched values are sole proprietorships (31.1%), corporations (18.7% - these can represent single individuals), and independent contractors (17.1%)
Part of the story appears to be the exclusion or inclusion of “LLC” or “INC” in one data source vs the other. Some company names are completely different, but probably representative of the same business, like these examples I gathered:
MTM GLASS LLC vs MTM GLASS CONCEPTS INC
DISCOVERY PARKING vs DISCOVERY PARKING PLUS LLC
NEIGHBORHOOD LLC vs THE NEIGHBORHOOD LLC
TREEHOUSE ACADEMY OF FERNANDINA BEACH LLC vs TREE HOUSE ACADEMY OF FERNANDINA BEACH LLC
And as noted, the rest missing are largely individuals - sole proprietors and independent contractors.
Understanding the missing data
This table shows percentages of the Florida PPP loan recipients that were not matched up with our corporate database:
Code
ppp_businesses_anti_joined %>% count(BusinessType) %>% arrange(desc(n)) %>% mutate(pct = 100*(n/sum(n)))Versus those that were matched up:
Code
ppp_businesses_anti_joined %>% count(BusinessType) %>% arrange(desc(n)) %>% mutate(pct = 100*(n/sum(n)))As I highlighted, clearly the crosswalk is missing some data about individuals, and, to a smaller extent, corporations.
Another method
As a last ditch, I tried something unconventional and removed all spaces, instances of “LLC”, and instances of “INC” before the join.
```{r}
#Columns: "business_name", "business_agent", "business_agent_address", "business_agent_city"
#For the sake of not having a single complicated regex expression:
florida_businesses_pruned <- florida_businesses %>% mutate(business_name = str_remove_all(business_name, "LLC"))
florida_businesses_pruned <- florida_businesses_pruned %>% mutate(business_name = str_remove_all(business_name, "INC"))
florida_businesses_pruned <- florida_businesses_pruned %>% mutate(business_name = str_remove_all(business_name, "[[:space:]]"))
ppp_florida_pruned <- ppp_florida %>% mutate(BorrowerName = str_remove_all(BorrowerName, "LLC"))
ppp_florida_pruned <- ppp_florida_pruned %>% mutate(BorrowerName = str_remove_all(BorrowerName, "INC"))
ppp_florida_pruned <- ppp_florida_pruned %>% mutate(BorrowerName = str_remove_all(BorrowerName, "[[:space:]]"))
``````{r}
ppp_pruned_joined <- ppp_florida_pruned %>% drop_na(BorrowerName) %>% inner_join(florida_businesses_pruned, by = c("BorrowerName" = "business_name"), keep=TRUE, na_matches = c("na", "never")) %>% select("BorrowerName","business_name","business_agent","business_agent_address","BorrowerAddress","business_agent_city","BorrowerCity", "BusinessType","Gender","Veteran","ForgivenessAmount")
```Although it had interesting results, this method was unreliable and only resulted in 3,195 unique rows out of 10,000. That’s not an improvement worth the significant errors it comes with.
Giving up on individual-level analysis
If I wanted to continue in this direction, I would keep the ppp_businesses_anti_joined data, which represents data not included in the ppp_businesses_joined dataframe, and try to match it directly to voter registration data to claw back some of the missing sample. After all, the idea of the corporation data ‘crosswalk’ originally was that it would let us glean the identity of the person behind the LLC or corporation when that information would otherwise be inaccessible.
However, at this point I lost faith in using individual level data. Instead, I completed this project using aggregate data - read below.
I just don’t see the individual-level data we have being appropriate for statistical analysis. Consider that the data we are working with at this stage is already 77% missing, with some groups more missing than others (so-called ‘MNAR’). Once we get to the voter registration join stage we lose even more data, resulting in a very lean dataframe closer to 600 (out of an originally sample of 10,000).
I have included the voter registration join process in the “Appendix” portion of this report.
Another way: Aggregate-level data
This class is about quantitative methods rather than data cleaning. So far I have spilled a lot of ink on dealing with Florida’s janky corporate database. Now it’s time for exciting statistical analysis, directly targeted at my research question!
To test the hypothesis, PPP loan forgiveness was given to registered Republicans more often than registered Democrats,, I will still use the 10,000 PPP loan applications in ppp_florida. But instead of joining them with voter registration data, I will just add aggregate information to new columns, and use those as control variables.
So, to add useful control variables, I have:
- Added a column for “percent Republican” using precinct level data from Harvard’s Dataverse on the results of the 2020 election. A value of .85 would mean the county voted 85% Republican in the 2020 election. This is called
county_percent_republican. - Added a column for GDP per county with data from the Bureau of Economic Analysis. This is called
county_gdp. - Added a column for “average revenue by business type” using data from the US Census. This is
NAICSAvgRevenue.
Below, I describe how they were calculated.
County-level political leaning
This tells me what the baseline for every county is in terms of partisanship.
```{r}
precincts <- read_csv("_data/2020-fl-precinct-general.csv", show_col_types = FALSE)
```Here is how I calculate the ‘redness’ of each county based on 2020 election results:
```{r}
dem_votes <- precincts %>% filter(office == "US PRESIDENT") %>% group_by(precinct) %>% filter(party_simplified == "DEMOCRAT") %>% select(c("precinct", "votes", "county_name"))
colnames(dem_votes) <- (c("precinct", "democatic_pres_votes", "county"))
repub_votes <- precincts %>% filter(office == "US PRESIDENT") %>% group_by(precinct) %>% filter(party_simplified == "REPUBLICAN") %>% select(c("precinct", "votes"))
colnames(repub_votes) <- (c("precinct", "repub_pres_votes"))
precincts_joined <- full_join(dem_votes, repub_votes, by = "precinct") %>% mutate(precinct_percent_republican = 100*(repub_pres_votes/sum(democatic_pres_votes, repub_pres_votes)))
precincts_total_dem <- precincts_joined %>% group_by(county) %>% summarise(sum(democatic_pres_votes))
colnames(precincts_total_dem) <- (c("COUNTYNAME", "dem_county_votes"))
precincts_total_repub <- precincts_joined %>% group_by(county) %>% summarise(sum(repub_pres_votes))
colnames(precincts_total_repub) <- (c("COUNTYNAME", "repub_county_votes"))
counties_joined <- full_join(precincts_total_dem, precincts_total_repub, by = "COUNTYNAME") %>% rowwise() %>% mutate(county_percent_republican = 100*(repub_county_votes/sum(dem_county_votes, repub_county_votes)))
counties_joined
```And here, I associate the counties with zip codes (which are in the rest of our data):
```{r}
zip_crosswalk <- read_csv("_data/ZIP-COUNTY-FIPS_2017-06.csv", show_col_types = FALSE)
#Remove periods for St. Lucie & St. Johns counties, make uppercase for matching with Zip data
zip_crosswalk <- zip_crosswalk %>% filter(STATE == "FL") %>% mutate(COUNTYNAME = toupper(str_remove(COUNTYNAME, " County"))) %>% mutate(COUNTYNAME = str_remove_all(COUNTYNAME, "\\.")) %>% select(c(ZIP, COUNTYNAME))
counties_zips <- zip_crosswalk %>% left_join(counties_joined, by = "COUNTYNAME")
counties_agg <- counties_zips %>% select(COUNTYNAME, dem_county_votes, repub_county_votes, county_percent_republican) %>% distinct()
```GDP by County
Say we eventually find that more loans got doled out to Republican counties. What if that’s because those Republican counties tend to have higher GDP? We should add GDP as a control variable.
This BEA data shows the result in “thousands of chained (2012) dollars”, meaning these are inflation-adjusted dollar ’equivalents` rather than today’s dollar amounts. The 2020 data has been selected.
```{r}
#| label: setup
#| output: false
#| warning: false
#| message: false
counties_gdp <- read_csv("_data/BEA_Florida_GDP_County.csv", show_col_types = FALSE, skip = 2)
counties_gdp <- counties_gdp[,c(1,4)]
colnames(counties_gdp) <- c('COUNTYNAME', 'county_gdp')
counties_gdp <- counties_gdp %>% mutate(COUNTYNAME = toupper(COUNTYNAME))
#Join with previous results
counties_agg <- counties_agg %>% left_join(counties_gdp, by = "COUNTYNAME")
```Here I tack that onto the data we are working with:
Code
#ppp_sample_joined <- ppp_florida %>% left_join(counties_agg, by = c("ProjectCountyName" = "COUNTYNAME"), match = "first")
#write_csv(ppp_sample_joined, "_data/ppp_sample_joined.csv")
#Below is for individual-level data:
#ppp_businesses_joined <- ppp_businesses_joined %>% left_join(counties_agg, by = c("ProjectCountyName" = "COUNTYNAME"), match = "first")
#ppp_businesses_anti_joined <- ppp_businesses_anti_joined %>% left_join(counties_agg, by = c("ProjectCountyName" = "COUNTYNAME"), match = "first")Here are the results of the operations above:
Code
ppp_sample_joined <- read_csv("_data/ppp_sample_joined.csv", show_col_types = FALSE)
ppp_sample_joinedAs an aside, it’s clear that there is a correlation between GDP and county Republican percentage. This may be due to the fact that Republican counties are less urban. So much for the idea that Republican counties have higher GDP! Either way, both are contained in the regression models to come.
Code
ggplot(ppp_sample_joined, aes(x = county_percent_republican, y = county_gdp)) +
geom_point() +
# scale_x_continuous(trans = 'log10') +
scale_y_continuous(trans = 'log10')+
#annotation_logticks(sides="lb") +
geom_smooth(method = "lm", se = FALSE) +
xlab("Log of County Pct. Republican") + ylab("County GDP")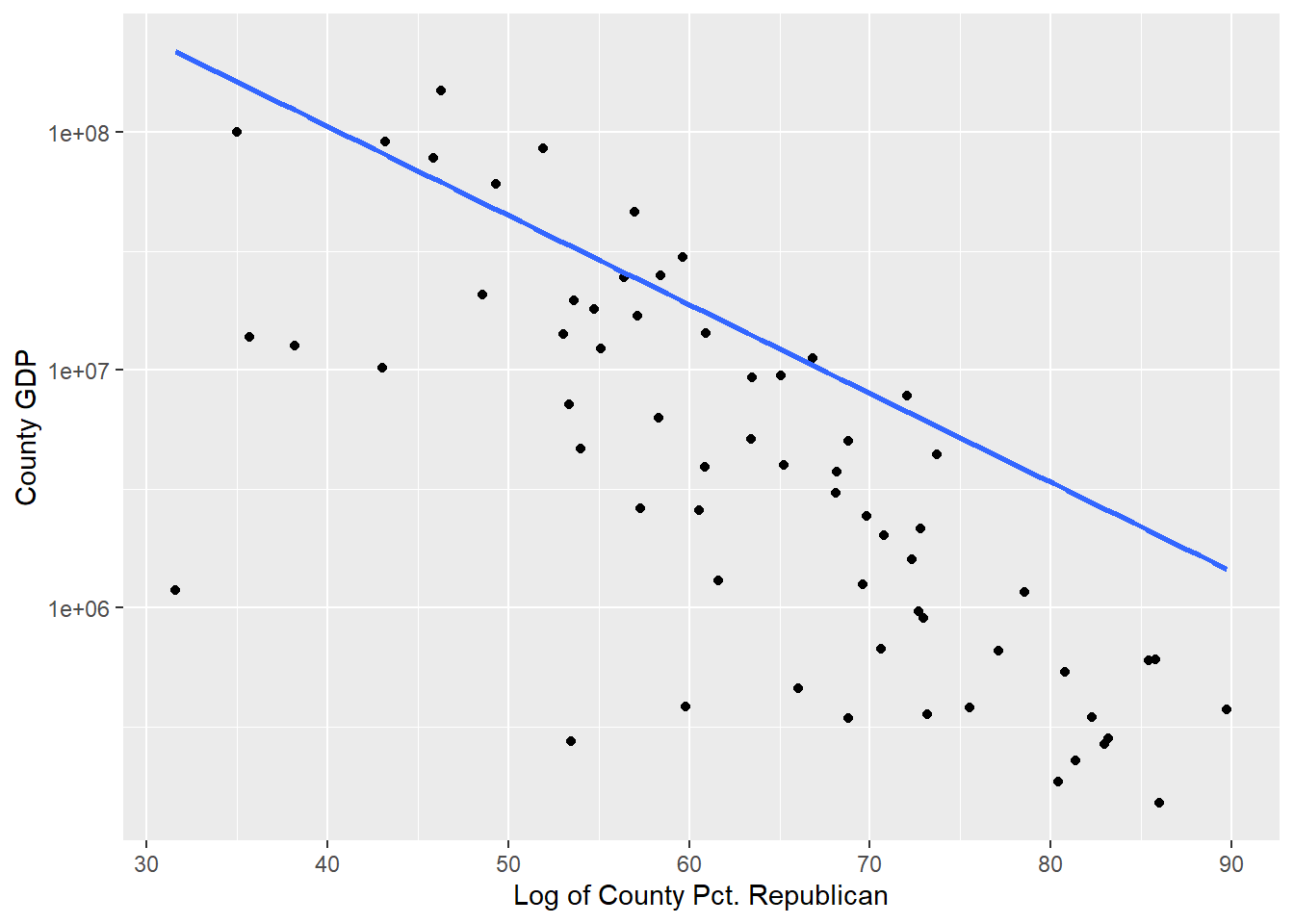
NAICS Codes
The North American Industry Classification System (NAICS) is a federal standard for evaluating which sector of the economy a business is in. For example, UMass Amherst has an NAICS code of 611310: “Colleges, Universities, and Professional Schools”.
Consider that a $300k loan would be extremely large for a picture-framing business but comparatively small for an aerospace or drilling company.
In our analysis, we expect the loan amount to vary by industry. Because of that, it’s important that the PPP data includes the NAICS code of every business that applied for PPP funds.
Upon read-in, the NAICS data is incorrectly interpreted as continuous data:
Code
is.factor(ppp_sample_joined$NAICSCode)[1] FALSEThis is corrected by using factor:
Code
ppp_sample_joined$NAICSCode <- factor(ppp_sample_joined$NAICSCode)
is.factor(ppp_sample_joined$NAICSCode)[1] TRUEImplicitly, we should acknowledge that JobsReported - the number of jobs the PPP loan was taken out to cover in the first place - is going to be the most meaningful predictor of loan size. Following basic common sense, it goes below in our first linear regression model. The second model here adds NAICSCode - now correctly interpreted as a categorical variable - as an additional predictor.
Code
#Drop 77 rows which have no NAICS code (out of ~10k) so we may compare using ANOVA later
#ppp_sample_joined <- ppp_sample_joined %>% drop_na(NAICSCode)
mod1 <- lm(ForgivenessAmount ~ JobsReported, data = ppp_sample_joined)
mod2 <- lm(ForgivenessAmount ~ JobsReported + NAICSCode, data = ppp_sample_joined)
summary(mod1)
Call:
lm(formula = ForgivenessAmount ~ JobsReported, data = ppp_sample_joined)
Residuals:
Min 1Q Median 3Q Max
-2467185 -12809 -5744 4931 4428693
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9580.39 1215.78 7.88 3.67e-15 ***
JobsReported 6386.91 54.09 118.09 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 108300 on 8714 degrees of freedom
(1284 observations deleted due to missingness)
Multiple R-squared: 0.6154, Adjusted R-squared: 0.6154
F-statistic: 1.395e+04 on 1 and 8714 DF, p-value: < 2.2e-16Code
#summary(mod2)An ANOVA shows that adding NAICSCode as a nominal variable with many levels is statistically worthwhile. Still, the many categorical values of NAICSCode are difficult to interpret and crowd the summary output. Pulling out the variables of interest and only focusing on them using R code would not be a statistical best practice. Optionally, I could target-encode these ‘nominal’ values, which is done by calculating the mean among the each category (using data drawn from this sample of 10k) and adding the results as numeric variables in my regression.
In my opinion, a better way is available: The U.S. Census’ latest “Economic Census” (2017) has already collected summary statistics of revenue according to NAICS type across different parts of the country, including Florida.
This additional data allows one to find the average revenue for a given kind of business in a given location in America. As one might assume, a surf shop in Miami is probably going to be more revenue-generating than a surf shop in Ohio.
So, for example, bringing this additional data in can tell us that the annual revenue for NAICS code “2508190” (child day care services) is $2,508,190, industry-wide, inside Florida. That will let us use NAICS information as numeric data rather than categorical data in our regression.
Here is the NAICS codebook for reference.
Adding NAICS average revenue
The sizable NAICS data must be pared down to only include Florida and only include six-digit NAICS codes like those found in our PPP data.
In the Census data, Florida is associated with many GEO_IDs, but there is always one commonality: the state code for Florida is 12, always preceded by US, (meaning United States). During EDA, I found that 04000US12 is the “parent” GEO_ID, inclusive of all other GEO_IDs (which represent subsets within Florida):
Code
naics_geo_index <- read_excel("_data/fl.xls")
head(naics_geo_index)In the next step, the entire 2017 Economic Census is read in. The file is pipe-delimited and contains 4.9m rows, with each row representing a summary statistic (part or whole, according to region):
```{r}
naics_census_all <- read_delim("_data/EC1700BASIC.dat", delim = "|")
```Next we strip this file down to the GEO_ID of 0400000US12, representing Florida summary statistics only. It is also necessary to filter out subset NAICS codes and other secondary information as noted below in code comments:
```{r}
#Filter out Florida NAICS codes and convert to dbl for joining:
naics_census_florida <- naics_census_all %>% filter(GEO_ID == "0400000US12")
naics_census_florida$NAICS2017 <- as.double(naics_census_florida$NAICS2017)
#Confirm that all NAICS codes in our PPP data are 6 digits for accuracy in joining:
#summary(ppp_sample_joined$NAICSCode)
#All NAICS codes are 6-digits in the PPP data, so we must filter out parent- and child- level NAICS codes:
naics_census_florida <- naics_census_florida %>% filter(nchar(NAICS2017) == 6)
#Choose the parent-level (most inclusive) "type of operation" (TYPOP). Here, 00 means 'all types' and other values are subsets.
naics_census_florida <- naics_census_florida %>% filter(TYPOP == "00")
#Select 'All establishments' rather than just 'Establishments subject to federal income tax'
naics_census_florida <- naics_census_florida %>% filter(TAXSTAT == "00")
#Get back to the original ppp_sample_joined, before we made NAICS code factor-type:
ppp_sample_joined <- ppp_florida %>% left_join(counties_agg, by = c("ProjectCountyName" = "COUNTYNAME"), match = "first")
ppp_sample_joined <- ppp_sample_joined %>% drop_na(NAICSCode)
#9923 rows before join:
nrow(ppp_sample_joined)
#9586 rows after join (3% non-match from NAICS lookup)
ppp_sample_joined <- ppp_sample_joined %>% inner_join(naics_census_florida, by = c("NAICSCode" = "NAICS2017"), na_matches = c("na", "never"), keep = TRUE)
ppp_sample_joined <- ppp_sample_joined %>% select("BorrowerName","BorrowerAddress","BorrowerCity","BusinessType","Gender","Veteran","JobsReported","NAICSCode","NAICS2017_TTL","county_percent_republican","county_gdp","RCPTOT","LoanStatus","ProjectCountyName","ForgivenessDate","InitialApprovalAmount","CurrentApprovalAmount","ForgivenessAmount")
#Zeroes should be replaced with NA:
ppp_sample_joined[, 12][ppp_sample_joined[, 12] == 0] <- NA
ppp_sample_joined <- ppp_sample_joined %>% rename(
NAICSAvgRevenue = RCPTOT,
NAICSDescription = NAICS2017_TTL)
#Return NAICSCode to categorical type since join is complete:
ppp_sample_joined$NAICSCode <- factor(ppp_sample_joined$NAICSCode)
ppp_sample_joined
#write_csv(ppp_sample_joined, "_data/ppp_sample_joined_naics.csv")
```Since the NAICS data was very large, here is the resulting data already joined:
Code
ppp_sample_joined <- read_csv("_data/ppp_sample_joined_naics.csv", show_col_types = FALSE)
ppp_sample_joinedWe did not end up pursuing individual-level data fully, but this is the code I also needed to run in order to prepare it, so I am including it for completeness:
```{r}
ppp_businesses_joined <- ppp_businesses_joined %>% inner_join(naics_census_florida, by = c("NAICSCode" = "NAICS2017"), na_matches = c("na", "never"), keep = TRUE)
ppp_businesses_joined <- ppp_businesses_joined %>% select("BorrowerName","BorrowerCity","BusinessType","business_agent_firstname"
,"business_agent_lastname","business_agent_address","Gender","Veteran","ForgivenessAmount","JobsReported","NAICSCode","NAICS2017_TTL","county_percent_republican","county_gdp","RCPTOT")
#Zeroes in the 15th column (RCPTOT) should be replaced with NA:
ppp_businesses_joined[, 15][ppp_businesses_joined[, 15] == 0] <- NA
ppp_businesses_joined <- ppp_businesses_joined %>% rename(
NAICSAvgRevenue = RCPTOT,
NAICSDescription = NAICS2017_TTL)
``````{r}
ppp_businesses_anti_joined <- ppp_businesses_anti_joined %>% inner_join(naics_census_florida, by = c("NAICSCode" = "NAICS2017"), na_matches = c("na", "never"), keep = TRUE)
ppp_businesses_anti_joined <- ppp_businesses_anti_joined %>% select("BorrowerName","BorrowerCity","BusinessType","Gender","Veteran","ForgivenessAmount","JobsReported","NAICSCode","NAICS2017_TTL","county_percent_republican","county_gdp","RCPTOT")
#Zeroes in the 15th column (RCPTOT) should be replaced with NA:
ppp_businesses_anti_joined[, 12][ppp_businesses_anti_joined[, 12] == 0] <- NA
ppp_businesses_anti_joined <- ppp_businesses_anti_joined %>% rename(
NAICSAvgRevenue = RCPTOT,
NAICSDescription = NAICS2017_TTL)
```Models: aggregate-level data
My hypothesis, suited to aggregate-level data, is that the loan amount varies by the political affiliation of the borrower.
Just to re-cap, these are the variables you will see below:
ForgivenessAmount - amount of loan forgiveness in dollars. In nearly all cases, this is the same as the original amount of the loan.
JobsReported - The number of jobs reported in the loan application
NAICSCode - Business type/sector
NAICSAvgRevenue - Average revenue (in dollars) of business type/sector
county_percent_republican - Percent of county that voted for Donald Trump in 2020 (example: .86 indicates very Republican county)
county_gdp - Gross Domestic Product of county, 2021
And here are some quick descriptive statistics about the variables we have included:
Code
ppp_sample_joined %>% select(JobsReported, county_gdp, county_percent_republican, NAICSAvgRevenue) %>% summary() JobsReported county_gdp county_percent_republican
Min. : 1.000 Min. : 150680 Min. :31.61
1st Qu.: 1.000 1st Qu.: 24488126 1st Qu.:43.22
Median : 1.000 Median : 85153512 Median :46.31
Mean : 6.113 Mean : 77586418 Mean :48.56
3rd Qu.: 4.000 3rd Qu.: 99667401 3rd Qu.:54.00
Max. :500.000 Max. :148725621 Max. :89.74
NA's :179 NA's :179
NAICSAvgRevenue
Min. : 458
1st Qu.: 725802
Median : 1719381
Mean : 5384191
3rd Qu.: 5794997
Max. :67922684
NA's :546 Following the theory, here are some models to start out with:
Code
mod1 <- lm(ForgivenessAmount ~ JobsReported, data = ppp_sample_joined)
mod2 <- lm(ForgivenessAmount ~ JobsReported + NAICSCode, data = ppp_sample_joined)
mod3 <- lm(ForgivenessAmount ~ JobsReported + NAICSAvgRevenue, data = ppp_sample_joined)
mod4 <- lm(ForgivenessAmount ~ JobsReported + NAICSAvgRevenue + county_percent_republican + county_gdp, data = ppp_sample_joined)Code
stargazer(mod1, mod2, mod3, mod4, type = "text")
==========================================================================================================================================
Dependent variable:
----------------------------------------------------------------------------------------------------------------
ForgivenessAmount
(1) (2) (3) (4)
------------------------------------------------------------------------------------------------------------------------------------------
JobsReported 6,481.323*** 6,476.746*** 6,443.538*** 6,465.206***
(55.350) (55.247) (57.348) (58.033)
NAICSCode -0.044***
(0.008)
NAICSAvgRevenue 0.001*** 0.001***
(0.0001) (0.0002)
county_percent_republican -243.162
(172.336)
county_gdp -0.00002
(0.00003)
Constant 9,617.185*** 33,920.120*** 6,092.851*** 19,586.500*
(1,251.268) (4,353.050) (1,534.729) (10,103.670)
------------------------------------------------------------------------------------------------------------------------------------------
Observations 8,339 8,339 7,881 7,725
R2 0.622 0.623 0.622 0.623
Adjusted R2 0.622 0.623 0.622 0.623
Residual Std. Error 109,243.400 (df = 8337) 109,028.100 (df = 8336) 112,057.100 (df = 7878) 112,855.900 (df = 7720)
F Statistic 13,711.480*** (df = 1; 8337) 6,899.831*** (df = 2; 8336) 6,488.756*** (df = 2; 7878) 3,194.459*** (df = 4; 7720)
==========================================================================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01At this point, it may appear that mod3 is a good model with reasonable R-squared and justifiable independent variables. But the diagnostic plot tells another story:
Code
par(mfrow = c(2,3)); plot(mod3, which = 1:6)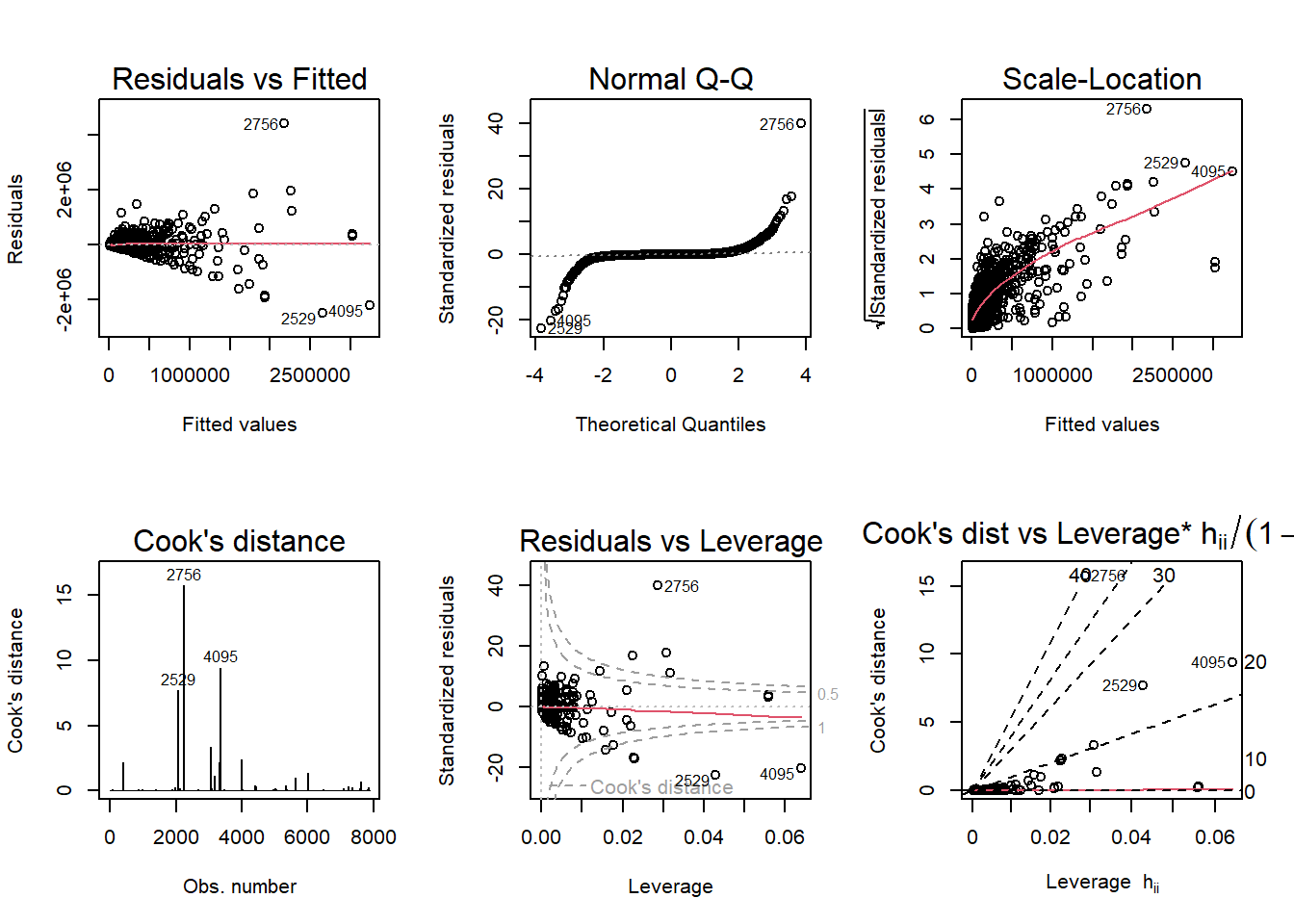
In these diagnostic plots,
-The Residuals vs Fitted graph shows a funnel shape, indicating heteroskedasticity (non-constant variance) in the residuals.
-The Scale-Location also indicates heteroskedasticity.
-The Normal Q-Q’s “S”-looking curve indicates non-normality in the error terms. The distribution of residuals is either skewed or peaked in the middle (high kurtosis).
-The Cook’s distance and leverage-related plots show dramatic outliers.
Transformations
A justification for ‘logging’ variables is obtained by looking at GGPairs(). Notice the sloped relationship between most independent variables and ForgivenessAmount.
Code
#|
ppp_sample_joined %>% select(ForgivenessAmount, JobsReported, county_percent_republican, NAICSAvgRevenue, county_gdp) %>% ggpairs(progress = FALSE)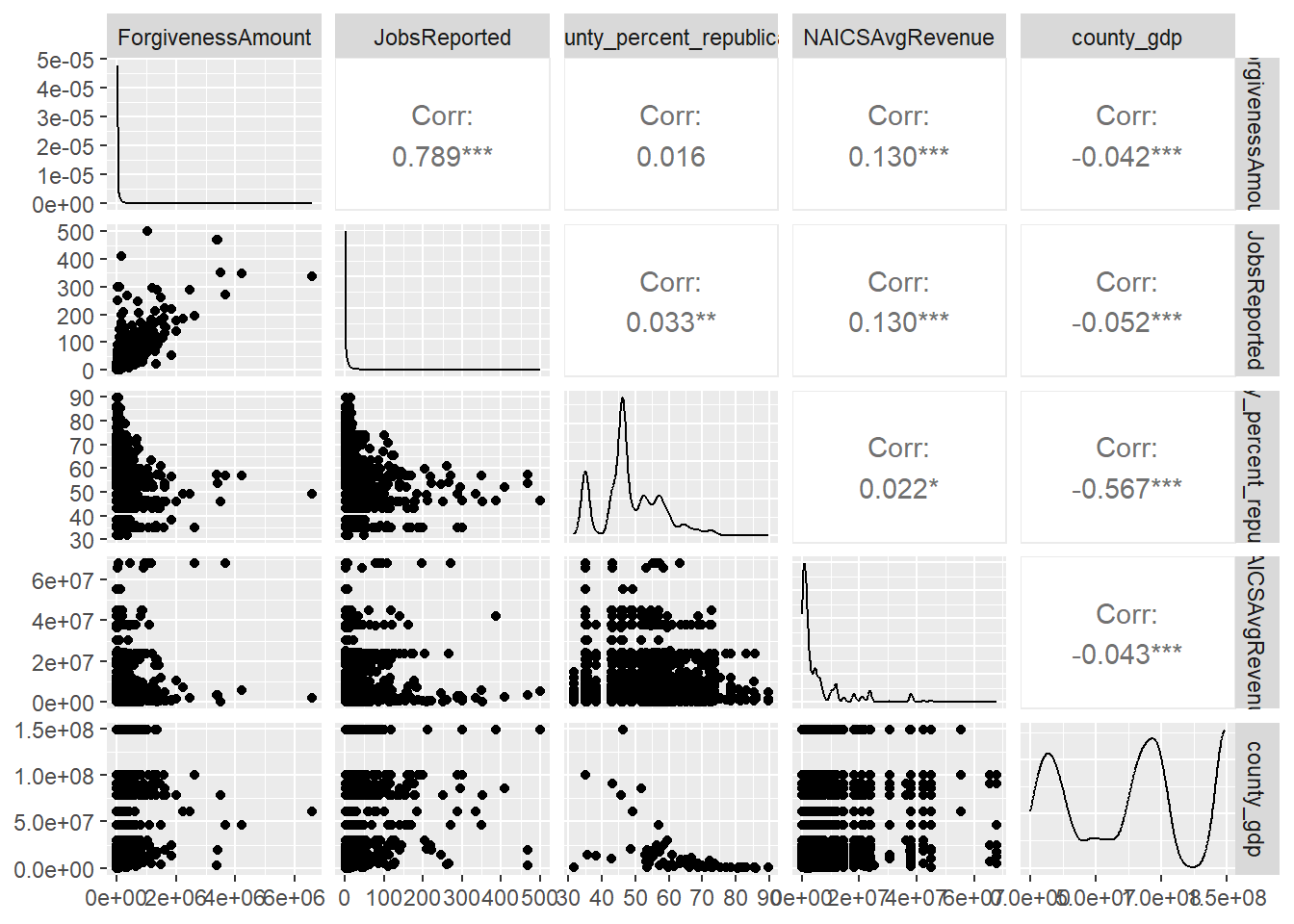
Logging both the predictor and response variables (except for NAICSAvgRevenue) returns our diagnostic plots to normal. The improved “log-log” model also lets us introduce county_gdp and see that it is a significant variable.
Code
mod3a <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue + county_gdp, data = ppp_sample_joined)
summary(mod3a)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue +
county_gdp, data = ppp_sample_joined)
Residuals:
Min 1Q Median 3Q Max
-4.6497 -0.5041 0.1240 0.7297 2.3516
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.974e+00 1.963e-02 457.093 < 2e-16 ***
log(JobsReported) 8.594e-01 8.304e-03 103.489 < 2e-16 ***
NAICSAvgRevenue 5.695e-09 1.133e-09 5.026 5.12e-07 ***
county_gdp 8.492e-10 1.884e-10 4.506 6.70e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8336 on 7721 degrees of freedom
(1861 observations deleted due to missingness)
Multiple R-squared: 0.6003, Adjusted R-squared: 0.6001
F-statistic: 3865 on 3 and 7721 DF, p-value: < 2.2e-16Code
par(mfrow = c(2,3)); plot(mod3a, which = 1:6)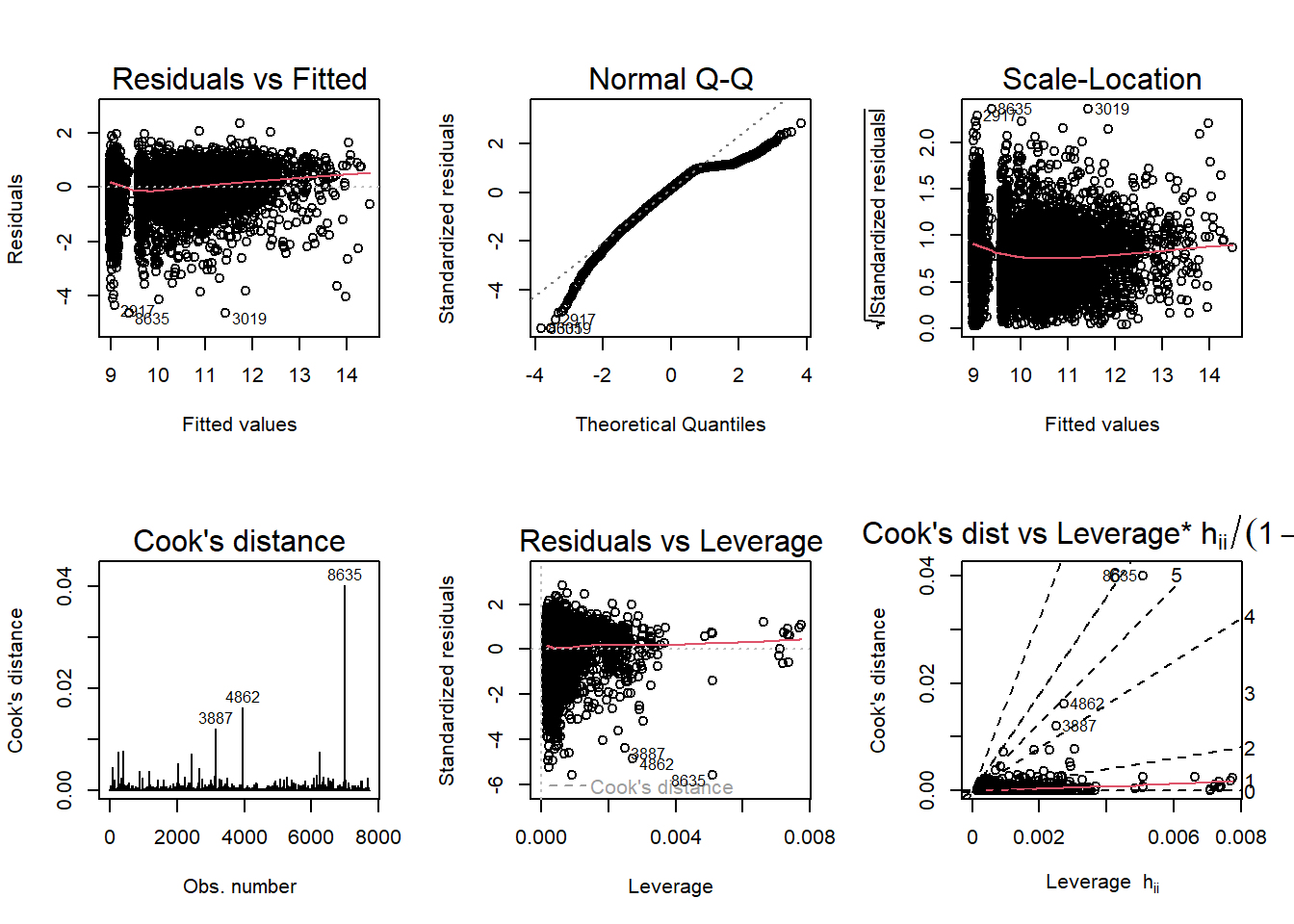
The Q-Q plot still show that there is a slight issue with normality (left skew in the distribution), and outliers are still shown in the Cook’s distance and Leverage-related plots. Still, there are not as many massive violations of assumptions of regression anymore.
Now we can bring in the county_percent_republican variable and finally start to answer our research question of “Is PPP loan forgiveness tied to political affiliation?”
The resulting model has a lower AIC, BIC, and higher R-squared than the previous model:
Code
mod3b <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue + log(county_gdp) + log(county_percent_republican), data = ppp_sample_joined)
par(mfrow = c(2,3)); plot(mod3b, which = 1:6)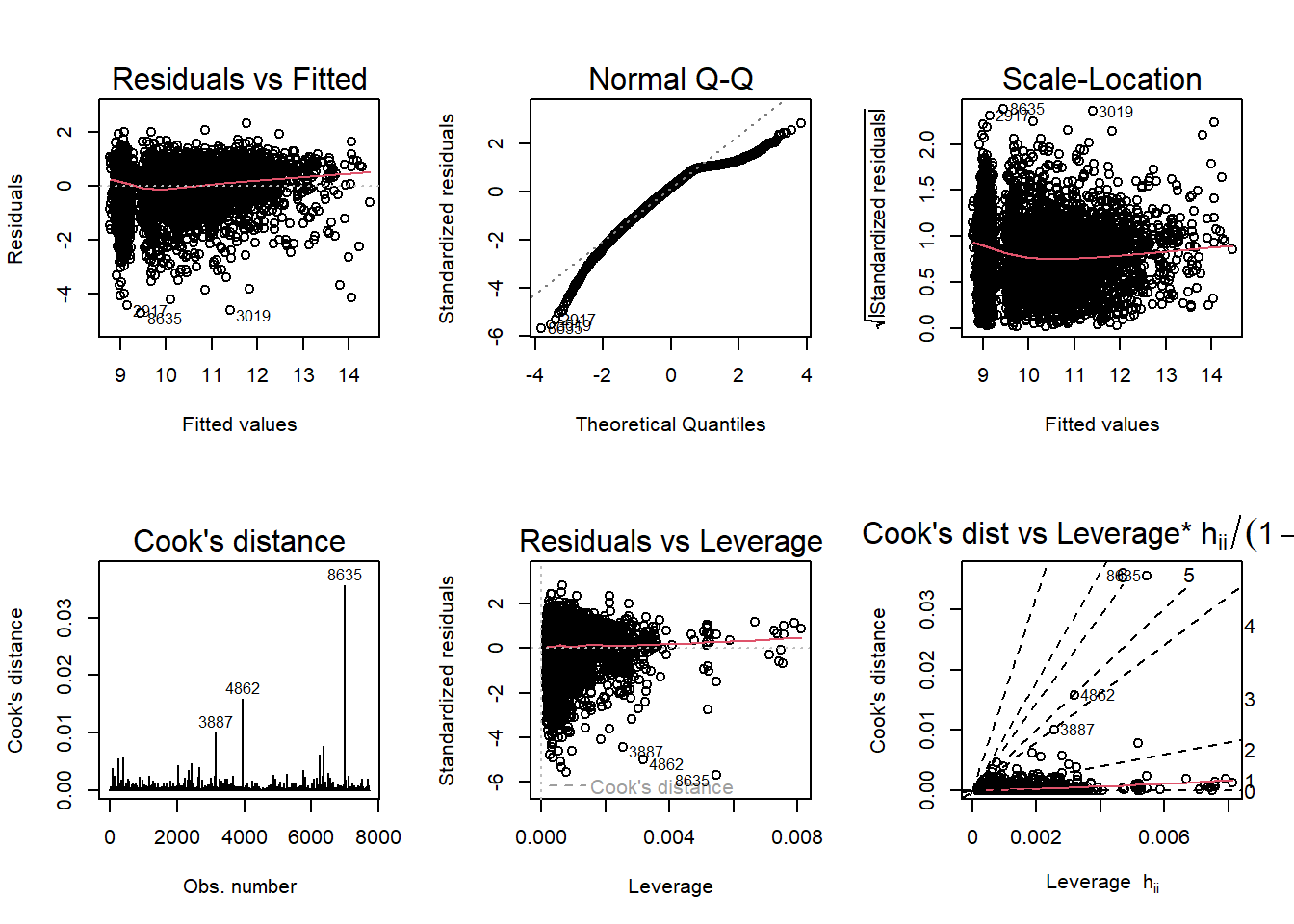
Code
summary(mod3b)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue +
log(county_gdp) + log(county_percent_republican), data = ppp_sample_joined)
Residuals:
Min 1Q Median 3Q Max
-4.7252 -0.5049 0.1317 0.7247 2.3285
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.792e+00 3.881e-01 25.229 < 2e-16 ***
log(JobsReported) 8.609e-01 8.279e-03 103.983 < 2e-16 ***
NAICSAvgRevenue 5.595e-09 1.131e-09 4.948 7.65e-07 ***
log(county_gdp) 1.878e-02 1.017e-02 1.846 0.0649 .
log(county_percent_republican) -2.806e-01 6.473e-02 -4.335 1.48e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.832 on 7720 degrees of freedom
(1861 observations deleted due to missingness)
Multiple R-squared: 0.6019, Adjusted R-squared: 0.6016
F-statistic: 2917 on 4 and 7720 DF, p-value: < 2.2e-16This ANOVA finds it to be statistically significant compared to the previous model:
Code
anova(mod3a, mod3b)Adding another version of the model with an interaction term between county_percent_republican and county_gdp is not much better, and I’d rather leave it out for a more ‘parsimonious’ model:
Code
mod3c <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue + log(county_gdp) + log(county_percent_republican) + log(county_percent_republican)*log(county_gdp), data = ppp_sample_joined)
par(mfrow = c(2,3)); plot(mod3c, which = 1:6)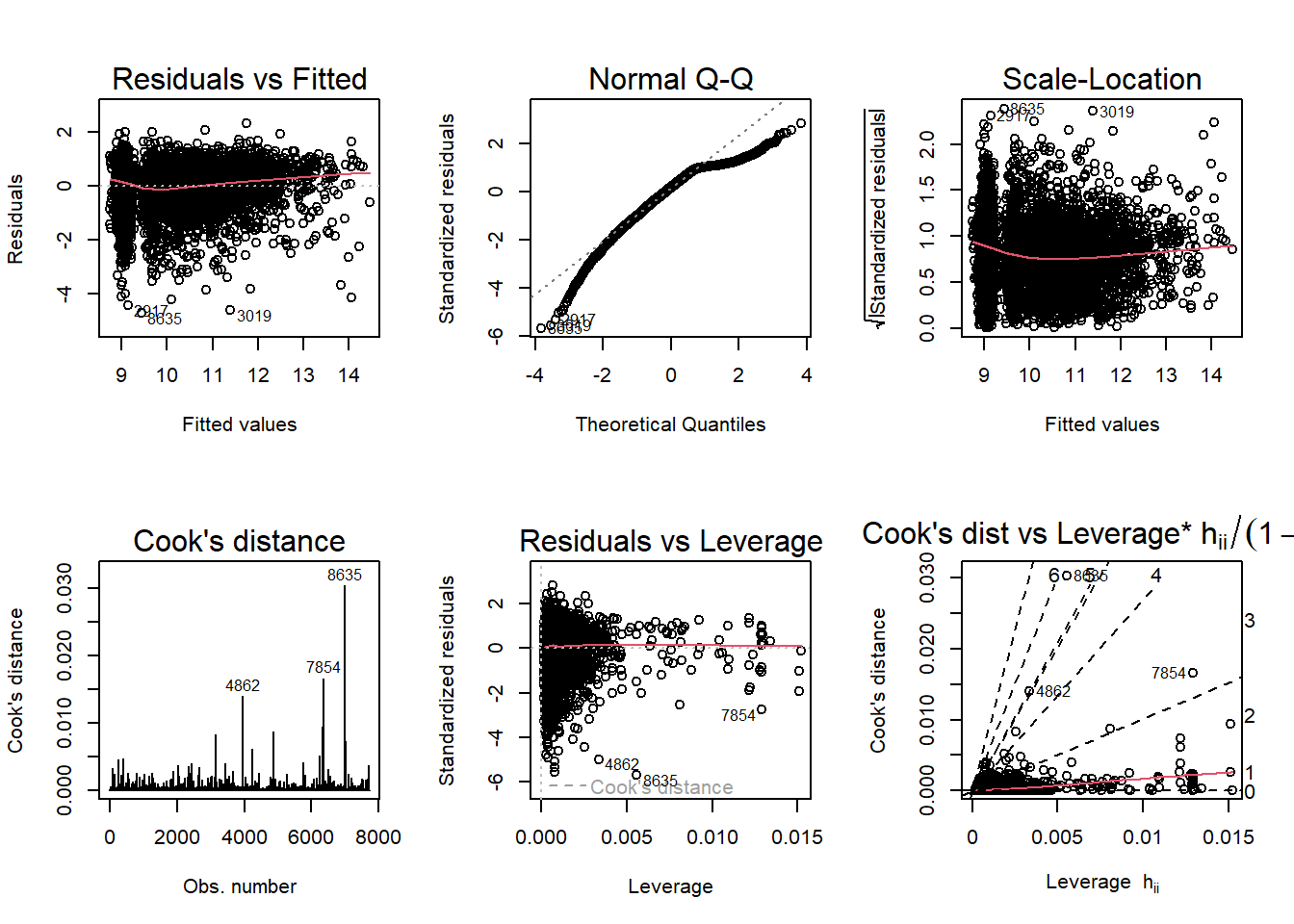
Code
summary(mod3c)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue +
log(county_gdp) + log(county_percent_republican) + log(county_percent_republican) *
log(county_gdp), data = ppp_sample_joined)
Residuals:
Min 1Q Median 3Q Max
-4.7228 -0.5071 0.1311 0.7251 2.3282
Coefficients:
Estimate Std. Error t value
(Intercept) 1.044e+01 2.619e+00 3.985
log(JobsReported) 8.608e-01 8.283e-03 103.929
NAICSAvgRevenue 5.598e-09 1.131e-09 4.950
log(county_gdp) -1.825e-02 1.491e-01 -0.122
log(county_percent_republican) -4.422e-01 6.524e-01 -0.678
log(county_gdp):log(county_percent_republican) 9.303e-03 3.738e-02 0.249
Pr(>|t|)
(Intercept) 6.82e-05 ***
log(JobsReported) < 2e-16 ***
NAICSAvgRevenue 7.58e-07 ***
log(county_gdp) 0.903
log(county_percent_republican) 0.498
log(county_gdp):log(county_percent_republican) 0.803
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8321 on 7719 degrees of freedom
(1861 observations deleted due to missingness)
Multiple R-squared: 0.6019, Adjusted R-squared: 0.6016
F-statistic: 2334 on 5 and 7719 DF, p-value: < 2.2e-16Here is the ANOVA test that does not find it to be significantly better:
Code
anova(mod3b, mod3c)And, overall, here is a summary of these log-log models, which are the most sound so far:
Code
stargazer(mod3a, mod3b, mod3c, type = "text")
==================================================================================================================================
Dependent variable:
-----------------------------------------------------------------------------------
log(ForgivenessAmount)
(1) (2) (3)
----------------------------------------------------------------------------------------------------------------------------------
log(JobsReported) 0.859*** 0.861*** 0.861***
(0.008) (0.008) (0.008)
NAICSAvgRevenue 0.000*** 0.000*** 0.000***
(0.000) (0.000) (0.000)
county_gdp 0.000***
(0.000)
log(county_gdp) 0.019* -0.018
(0.010) (0.149)
log(county_percent_republican) -0.281*** -0.442
(0.065) (0.652)
log(county_gdp):log(county_percent_republican) 0.009
(0.037)
Constant 8.974*** 9.792*** 10.437***
(0.020) (0.388) (2.619)
----------------------------------------------------------------------------------------------------------------------------------
Observations 7,725 7,725 7,725
R2 0.600 0.602 0.602
Adjusted R2 0.600 0.602 0.602
Residual Std. Error 0.834 (df = 7721) 0.832 (df = 7720) 0.832 (df = 7719)
F Statistic 3,864.826*** (df = 3; 7721) 2,917.464*** (df = 4; 7720) 2,333.700*** (df = 5; 7719)
==================================================================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01Model 3B (the middle one in the table above) looks to be the best model, and it actually finds a negative and significant relationship between Republican counties and forgiveness amount. This is not what I was expecting! My original (alternate) hypothesis was that Republicans received more loans than Democrats.
Interpretation
Since this is a log-log model, the way to interpret Model 3b would be: “holding county GDP, business type, and the number of jobs reported fixed, for every increase of one percent in Republican voting, we would expect to see a 0.28% decrease in the size of a PPP loan.”
In retrospect, it may have been better to re-frame the hypothesis as simply “political affiliation has an effect on PPP loan size”. If that was the case, I would say I have found support for the alternate hypothesis, and that the null hypothesis was rejected.
Although I have found evidence against the null hypothesis, I am not sure about the conclusiveness of this study. We are measuring political affiliation at the county level only. Business owners are probably more Republican than the county at-large.
Additionally, I should re-iterate that loan size (and its proxy, ForgivenessAmount) is in most cases simply a number picked by the loan applicant. We did not measure whether or not forgiveness was given - that would be a job for logistic regression. Instead, our sample was 100% comprised of businesses that got loan forgiveness. Indeed, loan forgiveness was guaranteed at the outset of the program. At the time of this writing, not all loans have been forgiven. Forgiveness status probably has more to do with the competence of the loan originator.
Using counties as predictors
During the poster session, one piece of feedback I received was that I could use the counties themselves as categorical independent variables.
Here, the counties are listed under the column ProjectCountyName. None of them appear to be significant, meaning no county is more predictive of loan outcome than another county.
Code
mod3d <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue + log(county_gdp) + log(county_percent_republican) + ProjectCountyName, data = ppp_sample_joined)
summary(mod3d)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue +
log(county_gdp) + log(county_percent_republican) + ProjectCountyName,
data = ppp_sample_joined)
Residuals:
Min 1Q Median 3Q Max
-4.7284 -0.4995 0.1339 0.7167 2.2468
Coefficients: (2 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.160e-01 1.234e+01 0.034 0.973
log(JobsReported) 8.593e-01 8.343e-03 102.990 < 2e-16 ***
NAICSAvgRevenue 5.550e-09 1.136e-09 4.887 1.04e-06 ***
log(county_gdp) 3.147e-01 4.718e-01 0.667 0.505
log(county_percent_republican) 9.327e-01 1.287e+00 0.725 0.469
ProjectCountyNameBAKER -1.417e-01 6.068e-01 -0.233 0.815
ProjectCountyNameBAY -4.308e-01 5.885e-01 -0.732 0.464
ProjectCountyNameBRADFORD -7.773e-01 9.551e-01 -0.814 0.416
ProjectCountyNameBREVARD -5.410e-01 8.016e-01 -0.675 0.500
ProjectCountyNameBROWARD -3.828e-01 8.671e-01 -0.441 0.659
ProjectCountyNameCALHOUN 1.679e-01 1.279e+00 0.131 0.896
ProjectCountyNameCHARLOTTE -2.483e-01 2.622e-01 -0.947 0.344
ProjectCountyNameCITRUS -5.991e-02 2.216e-01 -0.270 0.787
ProjectCountyNameCLAY -5.421e-01 3.523e-01 -1.539 0.124
ProjectCountyNameCOLLIER -3.427e-01 6.182e-01 -0.554 0.579
ProjectCountyNameCOLUMBIA -1.933e-01 2.539e-01 -0.761 0.446
ProjectCountyNameDIXIE -1.095e-02 9.760e-01 -0.011 0.991
ProjectCountyNameDUVAL -6.328e-01 1.056e+00 -0.599 0.549
ProjectCountyNameESCAMBIA -3.346e-01 6.513e-01 -0.514 0.607
ProjectCountyNameFLAGLER 1.706e-01 3.123e-01 0.546 0.585
ProjectCountyNameFRANKLIN -1.131e-01 1.065e+00 -0.106 0.915
ProjectCountyNameGADSDEN 1.274e+00 1.384e+00 0.920 0.357
ProjectCountyNameGILCHRIST 5.109e-01 9.047e-01 0.565 0.572
ProjectCountyNameGLADES 1.213e+00 1.220e+00 0.994 0.320
ProjectCountyNameGULF 5.155e-01 9.216e-01 0.559 0.576
ProjectCountyNameHAMILTON 1.851e-01 1.072e+00 0.173 0.863
ProjectCountyNameHARDEE 2.186e-01 6.074e-01 0.360 0.719
ProjectCountyNameHENDRY -1.445e-01 5.436e-01 -0.266 0.790
ProjectCountyNameHERNANDO -1.141e-01 2.096e-01 -0.544 0.586
ProjectCountyNameHIGHLANDS -1.339e-01 2.478e-01 -0.540 0.589
ProjectCountyNameHILLSBOROUGH -8.470e-01 1.280e+00 -0.662 0.508
ProjectCountyNameHOLMES -1.979e-01 7.206e-01 -0.275 0.784
ProjectCountyNameINDIAN RIVER 3.447e-02 2.512e-01 0.137 0.891
ProjectCountyNameJACKSON 7.023e-01 5.290e-01 1.327 0.184
ProjectCountyNameJEFFERSON 9.806e-01 1.431e+00 0.685 0.493
ProjectCountyNameLAFAYETTE -4.169e-01 1.199e+00 -0.348 0.728
ProjectCountyNameLAKE -3.912e-01 5.043e-01 -0.776 0.438
ProjectCountyNameLEE -7.174e-01 9.612e-01 -0.746 0.455
ProjectCountyNameLEON 2.033e-01 1.579e-01 1.287 0.198
ProjectCountyNameLEVY 6.107e-01 5.509e-01 1.108 0.268
ProjectCountyNameLIBERTY 1.292e+00 1.365e+00 0.947 0.344
ProjectCountyNameMADISON 2.472e-01 1.176e+00 0.210 0.834
ProjectCountyNameMANATEE -3.376e-01 4.726e-01 -0.714 0.475
ProjectCountyNameMARION -3.944e-01 5.421e-01 -0.728 0.467
ProjectCountyNameMARTIN -2.361e-01 2.012e-01 -1.174 0.241
ProjectCountyNameMIAMI-DADE -8.629e-01 1.399e+00 -0.617 0.537
ProjectCountyNameMONROE -9.627e-02 1.548e-01 -0.622 0.534
ProjectCountyNameNASSAU -3.219e-02 2.984e-01 -0.108 0.914
ProjectCountyNameOKALOOSA -4.807e-01 6.574e-01 -0.731 0.465
ProjectCountyNameOKEECHOBEE 1.303e-01 5.361e-01 0.243 0.808
ProjectCountyNameORANGE -6.325e-01 1.081e+00 -0.585 0.559
ProjectCountyNameOSCEOLA -1.580e-01 1.232e-01 -1.283 0.200
ProjectCountyNamePALM BEACH -5.559e-01 1.083e+00 -0.513 0.608
ProjectCountyNamePASCO -3.001e-01 4.543e-01 -0.660 0.509
ProjectCountyNamePINELLAS -7.635e-01 1.110e+00 -0.688 0.492
ProjectCountyNamePOLK -6.673e-01 8.538e-01 -0.782 0.434
ProjectCountyNamePUTNAM 8.153e-02 3.287e-01 0.248 0.804
ProjectCountyNameSANTA ROSA -2.375e-01 3.859e-01 -0.615 0.538
ProjectCountyNameSARASOTA -4.373e-01 6.349e-01 -0.689 0.491
ProjectCountyNameSEMINOLE -2.353e-01 5.378e-01 -0.438 0.662
ProjectCountyNameSUMTER -2.409e-01 2.809e-01 -0.858 0.391
ProjectCountyNameSUWANNEE -1.437e-01 3.527e-01 -0.407 0.684
ProjectCountyNameTAYLOR -3.279e-01 8.034e-01 -0.408 0.683
ProjectCountyNameUNION 1.472e-01 1.209e+00 0.122 0.903
ProjectCountyNameVOLUSIA -4.749e-01 6.451e-01 -0.736 0.462
ProjectCountyNameWAKULLA 1.327e-01 8.002e-01 0.166 0.868
ProjectCountyNameWALTON NA NA NA NA
ProjectCountyNameWASHINGTON NA NA NA NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8322 on 7659 degrees of freedom
(1861 observations deleted due to missingness)
Multiple R-squared: 0.6049, Adjusted R-squared: 0.6015
F-statistic: 180.4 on 65 and 7659 DF, p-value: < 2.2e-16Here is the diagnostic plot. Some counties which only were associated with one loan application are left out:
Code
par(mfrow = c(2,3)); plot(mod3d, which = 1:6)Warning: not plotting observations with leverage one:
1774, 5507, 6529, 6668, 7183
Warning: not plotting observations with leverage one:
1774, 5507, 6529, 6668, 7183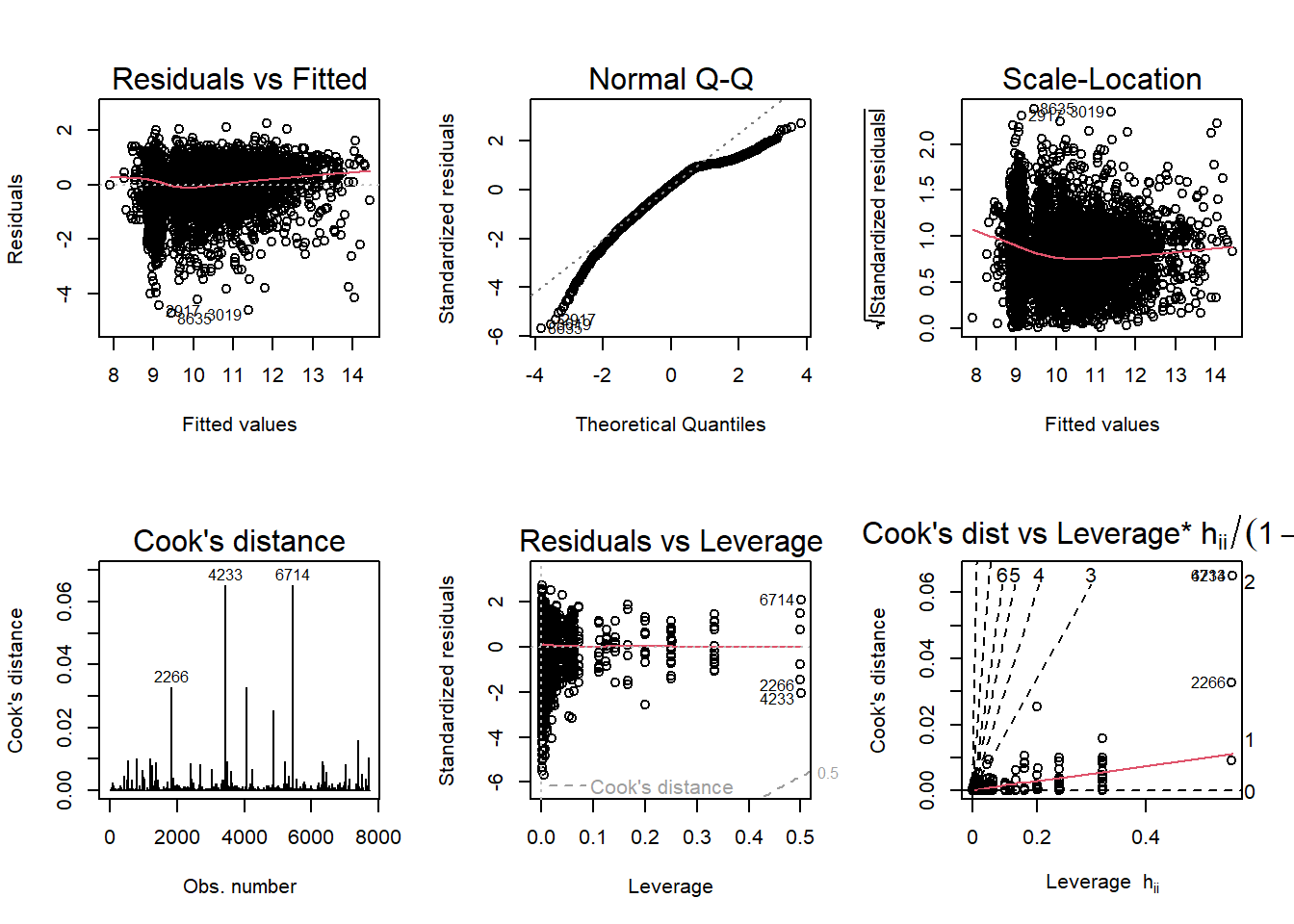
The diagnostic plots look OK, but the model is telling us that nothing is significant about which counties the loans originated in.
Appendix
Back to the original research design! Feel free to stop reading here - the information below continues to use the individual-level data that we have ‘given up on’ earlier.
I feel it is important to include because these methods could be used in a state that has better-quality data.
Voter registration data
Voter registration data was mailed to me on DVD-ROM by Florida’s state government. Unfortunately, data from 2020 was not available - just data from 2022. This means that politically significant events like the Jan 6th 2021 Capitol insurrection have already had an effect on these voters - we may not be measuring the same voters as before.
With that said, I suspect that voter registration is a durable barometer of lifelong political affiliation, especially in a state like Florida, which has seen a shift rightward since 2020.
This loop reads the fixed-width files (which have a different composition than the corporation/fictitious name files) and writes them to a CSV:
```{r}
setwd("_data\\florida_voter_data\\20221102_VoterDetail")
fileNames <- Sys.glob("*.txt")
for (fileName in fileNames) {
voters <- read.table(
fileName,
sep="\t", header=FALSE, fill = TRUE, quote = "")
write.table(voters,
"florida_voters.csv",
append = TRUE,
sep = ",",
row.names = FALSE,
col.names = FALSE)
}
```And we can read it in:
```{r}
florida_voters_all <- read_csv("_data\\florida_voter_data\\20221102_VoterDetail\\florida_voters.csv", col_names = FALSE)
```This function checks to make sure all lines were read into the dataframe florida_voters_all.
```{r}
setwd("_data\\florida_voter_data\\20221102_VoterDetail")
filenames <- dir(pattern = "[.]txt$")
df <- sapply(filenames, function(x) length(count.fields(x, sep = "\1")))
```Using Postgres SQL
The 15+ million rows were too much to join using Rstudio on my computer. Due to size and memory constraints, I needed to use Postgres SQL. This required a database connection in RStudio.
```{r}
library(RPostgres)
con <- dbConnect(RPostgres::Postgres(), user = 'postgres', password = '####')
```Tables were written to Postgres from R:
```{r}
dbWriteTable(
con,
name = "florida_voters_all",
value = florida_voters_all,
row.names = TRUE,
overwrite = FALSE,
append = FALSE,
field.types = NULL,
temporary = FALSE,
copy = NULL
)
``````{r}
dbWriteTable(
con,
name = "ppp_businesses_joined",
value = ppp_businesses_joined,
row.names = TRUE,
overwrite = FALSE,
append = FALSE,
field.types = NULL,
temporary = FALSE,
copy = NULL
```Joining in Postgres SQL
This SQL join matched voters to the PPP businesses on the registered agent’s first name, last name, and first 3 characters of their address.
```{sql}
select firstname, lastname, "business_name", "ForgivenessAmount", "business_agent_address", address, registration, email into ppp_voters from florida_voters_all fva
inner join ppp_businesses_joined pbj
on UPPER(pbj.business_agent_firstname) = UPPER(fva.firstname) and UPPER(pbj.business_agent_lastname) = UPPER(fva.lastname) and UPPER(LEFT(pbj.business_agent_address, 3)) = UPPER(LEFT(fva.address, 3))
```The resulting table, ppp_voters, came back with 616 rows. It’s interesting, if impractical due to its small size. We see that there are more Republicans in this dataset than Democrats, with 41.9% vs 28.6% respectively.
Code
#ppp_voters <- dbReadTable(con, "ppp_voters")
ppp_voters <- read_csv("_data/ppp_voters.csv", show_col_types = FALSE)
print(summarytools::dfSummary(ppp_voters$registration,
varnumbers = FALSE,
plain.ascii = FALSE,
style = "grid",
graph.magnif = 0.70,
valid.col = FALSE),
method = 'render',
table.classes = 'table-condensed')Data Frame Summary
ppp_voters
Dimensions: 616 x 1Duplicates: 609
| Variable | Stats / Values | Freqs (% of Valid) | Graph | Missing | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| registration [character] |
|
|
12 (1.9%) |
Generated by summarytools 1.0.1 (R version 4.2.2)
2022-12-18
Models
Here are models which test the original alternate hypothesis, H1.
This one is log(ForgivenessAmount) ~ log(JobsReported):
Code
mod4 <- lm(ForgivenessAmount ~ JobsReported, data = ppp_voters)
mod5 <- lm(log(ForgivenessAmount) ~ log(JobsReported), data = ppp_voters)
par(mfrow = c(2,3)); plot(mod5, which = 1:6)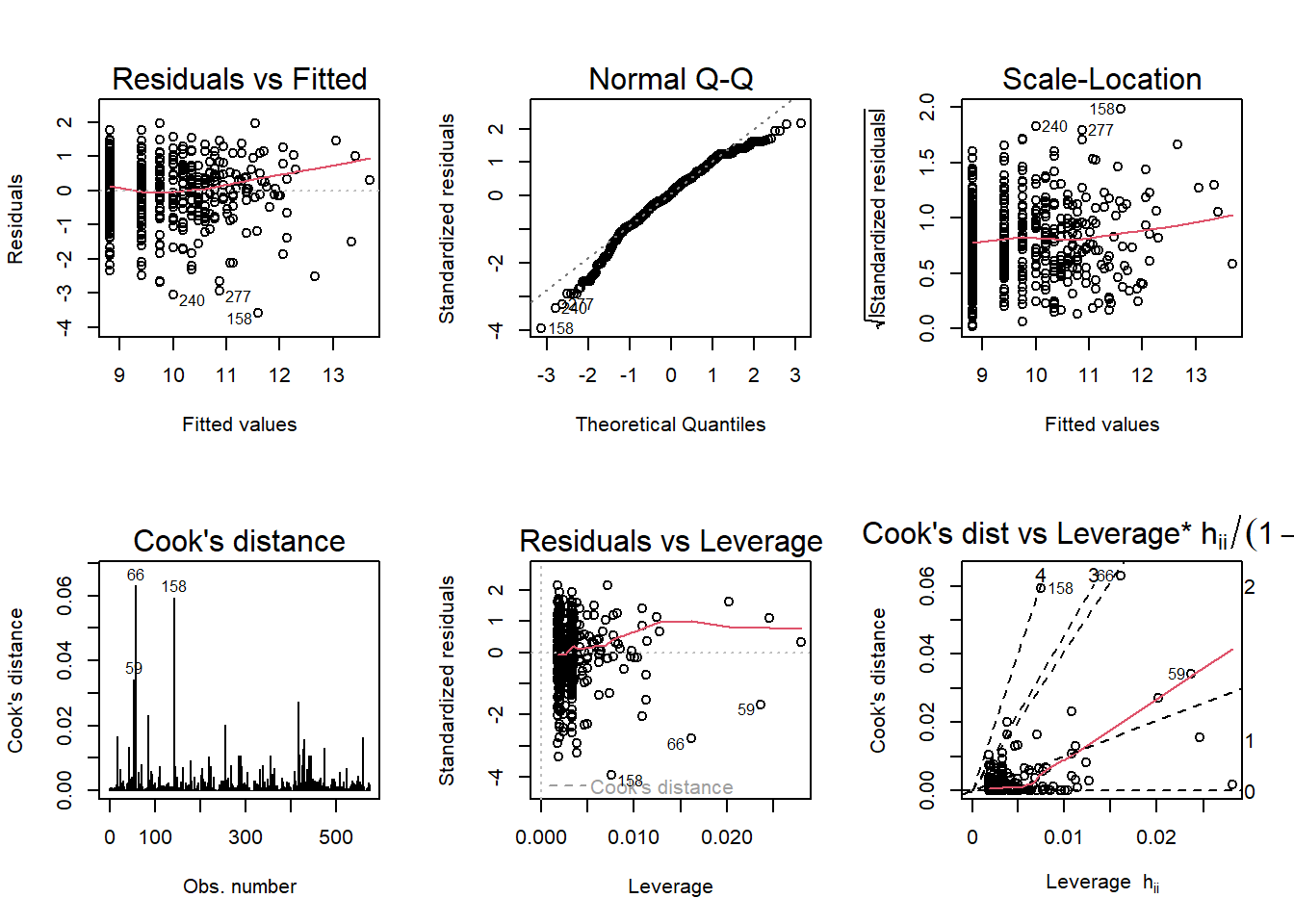
Code
summary(mod5)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported), data = ppp_voters)
Residuals:
Min 1Q Median 3Q Max
-3.5895 -0.5279 0.0512 0.6482 1.9533
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.81600 0.05211 169.17 <2e-16 ***
log(JobsReported) 0.85615 0.03221 26.58 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9112 on 571 degrees of freedom
(43 observations deleted due to missingness)
Multiple R-squared: 0.553, Adjusted R-squared: 0.5522
F-statistic: 706.4 on 1 and 571 DF, p-value: < 2.2e-16And log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue
Code
mod5a <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue, data = ppp_voters)
summary(mod5a)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue,
data = ppp_voters)
Residuals:
Min 1Q Median 3Q Max
-3.4049 -0.4988 0.0489 0.6844 2.0627
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.757e+00 5.414e-02 161.751 < 2e-16 ***
log(JobsReported) 8.152e-01 3.408e-02 23.920 < 2e-16 ***
NAICSAvgRevenue 1.550e-08 4.629e-09 3.349 0.000867 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.903 on 555 degrees of freedom
(58 observations deleted due to missingness)
Multiple R-squared: 0.5602, Adjusted R-squared: 0.5586
F-statistic: 353.4 on 2 and 555 DF, p-value: < 2.2e-16Code
par(mfrow = c(2,3)); plot(mod5a, which = 1:6)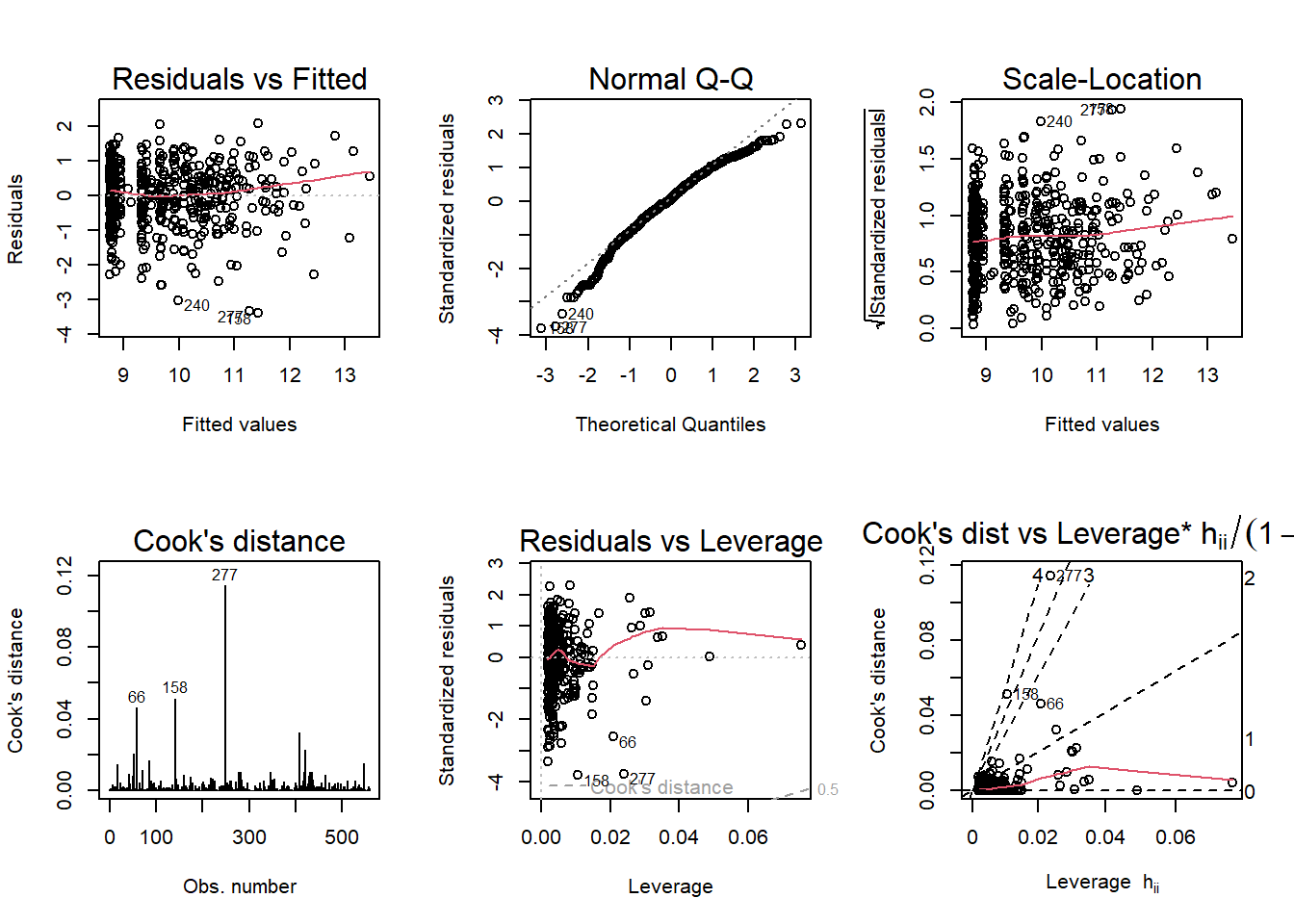
It was necessary to relevel the registration information in order to get output for Democrats and Republicans. I used “NPA” - no party affiliation.
Code
ppp_voters$registration <- factor(ppp_voters$registration, ordered = FALSE )
ppp_voters$registration <- relevel(ppp_voters$registration, ref = 'NPA')
mod5b <- lm(log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue + registration, data = ppp_voters)
summary(mod5b)
Call:
lm(formula = log(ForgivenessAmount) ~ log(JobsReported) + NAICSAvgRevenue +
registration, data = ppp_voters)
Residuals:
Min 1Q Median 3Q Max
-3.3771 -0.5206 0.0588 0.6613 2.1170
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.700e+00 8.329e-02 104.455 < 2e-16 ***
log(JobsReported) 8.086e-01 3.406e-02 23.739 < 2e-16 ***
NAICSAvgRevenue 1.649e-08 4.630e-09 3.561 0.000402 ***
registrationDEM 1.268e-01 1.029e-01 1.233 0.218266
registrationGRE 1.148e-01 6.391e-01 0.180 0.857530
registrationIND 2.058e-01 4.073e-01 0.505 0.613631
registrationLPF 1.983e-01 5.229e-01 0.379 0.704634
registrationREP 4.990e-02 9.345e-02 0.534 0.593536
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.896 on 541 degrees of freedom
(67 observations deleted due to missingness)
Multiple R-squared: 0.5667, Adjusted R-squared: 0.5611
F-statistic: 101.1 on 7 and 541 DF, p-value: < 2.2e-16Code
par(mfrow = c(2,3)); plot(mod5b, which = 1:6)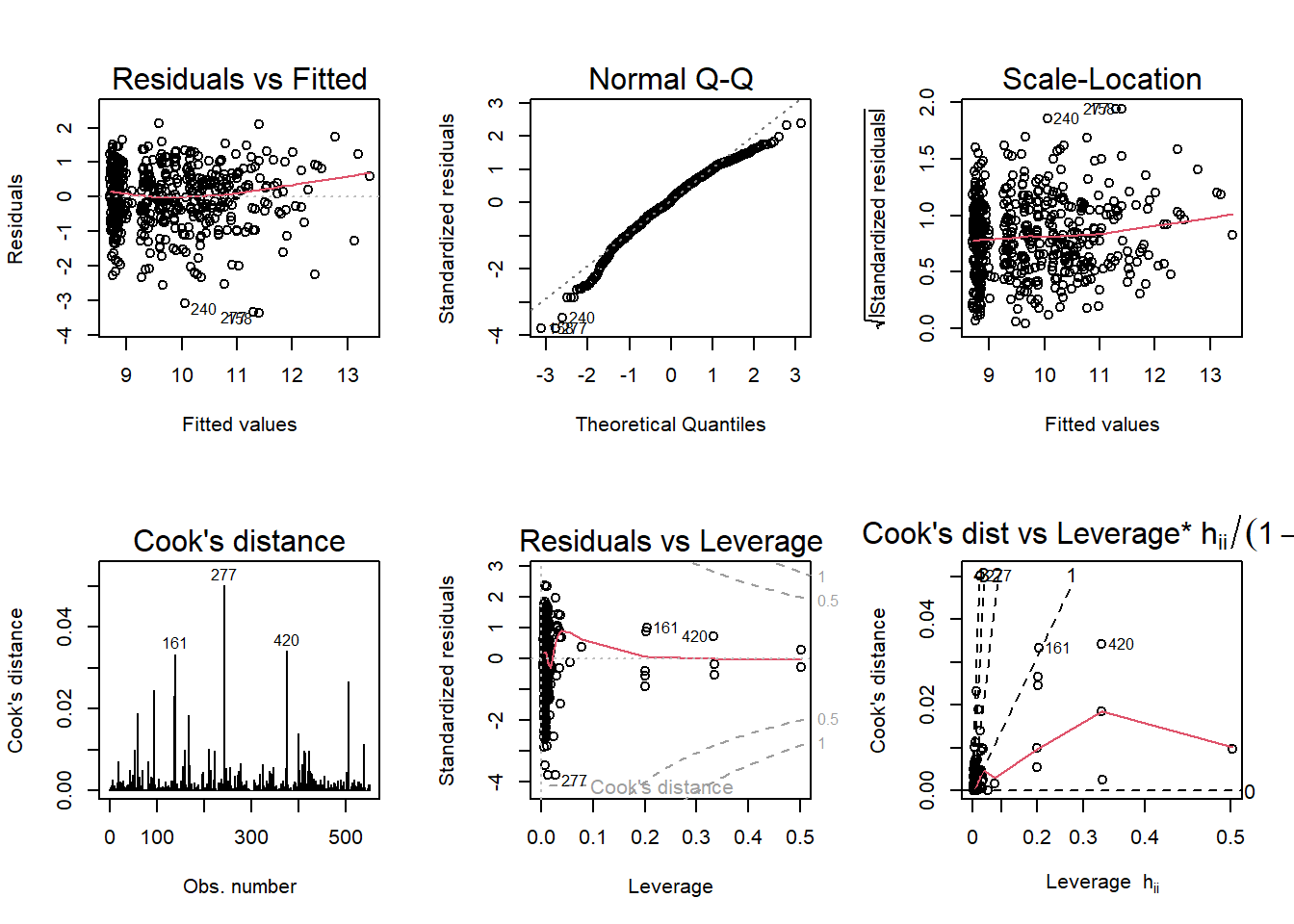
And here is the output of those models, with Model 5B showing that there is no statistically significant link between voter registration and loan forgiveness amount (with our limited individual-level data):
Code
stargazer(mod5, mod5a, mod5b, type = "text")
==============================================================================================
Dependent variable:
--------------------------------------------------------------------------
log(ForgivenessAmount)
(1) (2) (3)
----------------------------------------------------------------------------------------------
log(JobsReported) 0.856*** 0.815*** 0.809***
(0.032) (0.034) (0.034)
NAICSAvgRevenue 0.00000*** 0.00000***
(0.000) (0.000)
registrationDEM 0.127
(0.103)
registrationGRE 0.115
(0.639)
registrationIND 0.206
(0.407)
registrationLPF 0.198
(0.523)
registrationREP 0.050
(0.093)
Constant 8.816*** 8.757*** 8.700***
(0.052) (0.054) (0.083)
----------------------------------------------------------------------------------------------
Observations 573 558 549
R2 0.553 0.560 0.567
Adjusted R2 0.552 0.559 0.561
Residual Std. Error 0.911 (df = 571) 0.903 (df = 555) 0.896 (df = 541)
F Statistic 706.362*** (df = 1; 571) 353.407*** (df = 2; 555) 101.084*** (df = 7; 541)
==============================================================================================
Note: *p<0.1; **p<0.05; ***p<0.01In this version of the data, we do not find any support for an alternate hypothesis and fail to reject the null hypothesis.
Sources
Duchin, R., & Hackney, J. (2021). Buying the Vote? The Economics of Electoral Politics and Small-Business Loans. Journal of Financial and Quantitative Analysis, 56(7), 2439-2473. doi:10.1017/S002210902100048X
Chernenko, S., & Scharfstein, D. (2022, February). National Bureau of Economic Research | NBER. RACIAL DISPARITIES IN THE PAYCHECK PROTECTION PROGRAM. Retrieved October 10, 2022, from https://www.nber.org/system/files/working_papers/w29748/w29748.pdf
MIT Election Data and Science Lab, 2022, “Precinct-Level Returns 2020 by Individual State”, https://doi.org/10.7910/DVN/NT66Z3, Harvard Dataverse, V2, UNF:6:DZkrbNb8jFLYglz5rTqxWA== [fileUNF]
U.S. Bureau of Economic Analysis (BEA), “GDP by County, Metro, and Other Areas.” 2020, https://www.bea.gov/data/gdp/gdp-county-metro-and-other-areas.
U.S. Census Bureau. “Economic Census (2017, 2012, 2007, 2002).” Census.gov, 28 Oct. 2021,https://www.census.gov/data/developers/data-sets/economic-census.html.