HW3_EmmaRasmussen

hw3

Author

Emma Rasmussen

Published

October 31, 2022

knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)

library(tidyverse)
library(ggplot2)
library(dplyr)
library(stringr)
library(alr4)
library(smss)
library(stargazer)

Error in library(stargazer): there is no package called 'stargazer'

1.1.1

The predictor is ppgdp, and the response variable is fertility. ## 1.1.2

data(list="UN11")

plot(x=UN11$ppgdp, y=UN11$fertility)

A straight line function would not be a good model for this graph. It appears that ppgdp has the biggest impact on fertility towards the left side of the graph (closer to x=0). In other words, ppgd has the biggest impact on fertility in lower ppgdp values and then does not change as drastically as ppgdp gets even larger (right side of the graph). ## 1.1.3

plot(x=log(UN11$ppgdp), y=log(UN11$fertility))

A logarithmic function makes a lot more sense for this data frame in order to apply a linear regression model. When both variables are logged, the data appears more linear and has a negative trend.

2a

I created an example data frame to explore this question. According to the output of the lm() function, the slopes are different (the one multiplied by 1.33 has a greater slope). The plots appear to have the same slope, however the y scale is different which likely explains why the lm() function gives different slopes.

dfexample<-data.frame(col1=c(2004, 2005, 2006, 2007, 2008, 2009, 2010),
col2=c(50000, 56000, 70000, 68000, 58000, 72000, 80000),
col3=col2*1.33)

Error in data.frame(col1 = c(2004, 2005, 2006, 2007, 2008, 2009, 2010), : object 'col2' not found

dfexample

Error in eval(expr, envir, enclos): object 'dfexample' not found

lm(col2~ col1, data=dfexample)

Error in is.data.frame(data): object 'dfexample' not found

lm(col3~ col1, data=dfexample)

Error in is.data.frame(data): object 'dfexample' not found

fit2<-lm(col2~ col1, data=dfexample)

Error in is.data.frame(data): object 'dfexample' not found

fit3<-lm(col3~ col1, data=dfexample)

Error in is.data.frame(data): object 'dfexample' not found

summary(fit2)

Error in summary(fit2): object 'fit2' not found

summary(fit3)

Error in summary(fit3): object 'fit3' not found

plot(x=dfexample$col1, y=dfexample$col2)

Error in plot(x = dfexample$col1, y = dfexample$col2): object 'dfexample' not found

plot(x=dfexample$col1, y=dfexample$col3)

Error in plot(x = dfexample$col1, y = dfexample$col3): object 'dfexample' not found

2b

The correlation (adjusted R squared) is the same for both models. See above.

3

data(list="water")
pairs(water[2:8])

I don’t know if I am interpreting this correctly but using this matrix we can see which site correlates most closely with stream runoff (BSAAM). Using this matrix, we see there is a strong correlation between OPSLAKE, OPRC and OPBPC site precipitation and runoff. Perhaps precipitation measured at these sites could predict runoff. Moving forward, I might fit a models using those three sites to predict runoff at the site near bishop and figure out which model creates the best prediction (has the highest F statistic).

4

data(list="Rateprof")
pairs(Rateprof[8:12])

There is a strong positive correlation between quality and helpfulness, quality and clarity, and clarity and helpfulness. In other words, professors that rate high in one of these areas are likely to rate high in the others. easiness is less strongy correlated with quality, helpfulness and clarity, but there is still a positive relationship (i.e. professors with “easy” courses are more likely to rate higher in other categories but this trend is less strong). Finally, raterInterest does not predict the other ratings very well. Easiness does not appears to have much of a correlation with rater interest. There is a positive relationship between rater interest and quality, helpfulness, and clarity, but again it is not a strong relationship.

##5a

data(list="student.survey")
ggplot(student.survey, aes(x=re, y=pi)) +geom_point()

ggplot(student.survey, aes(x= tv, y=hi))+geom_point()+geom_smooth(method="lm")

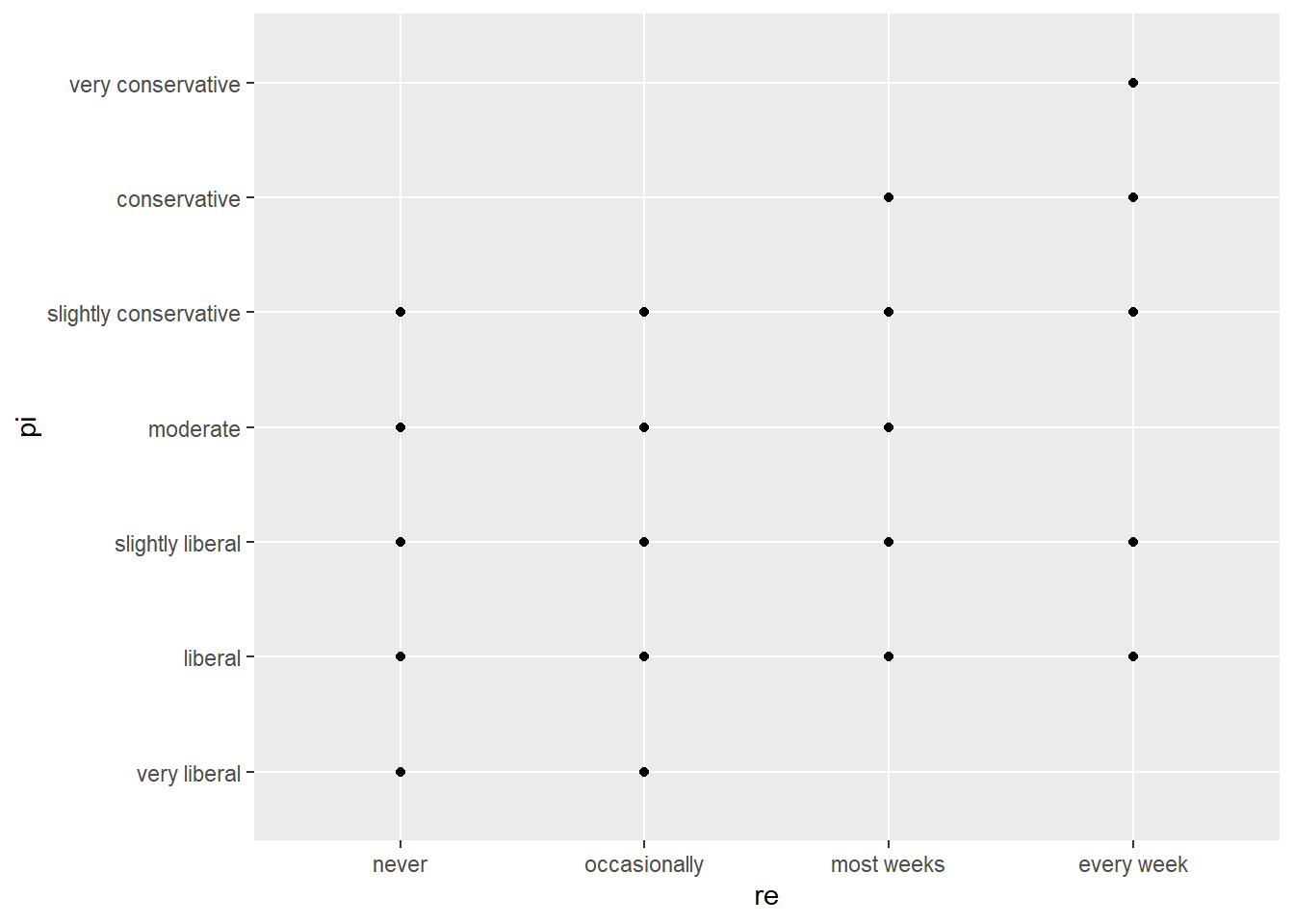
Political Affiliation and Religiosity: This graph is not super useful given there are multiple observations contained in each point on the graph but even so, it appears that more frequently attending religious services correlates with more conservative political ideology.

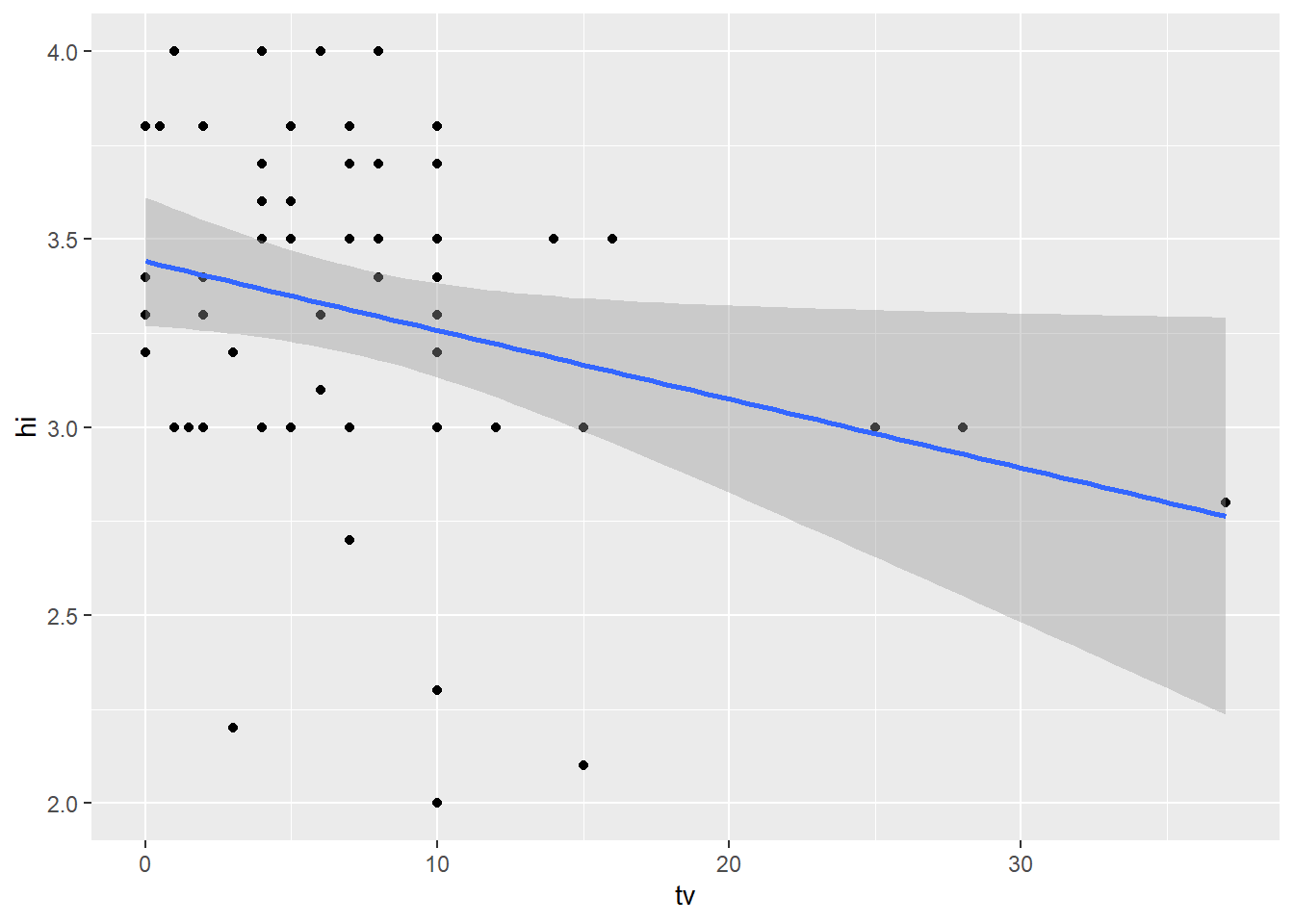
TV and GPA: There appears to be a negative correlation between time spent watching tv and high school gpa.

##5b

student.survey

   subj ge ag  hi  co   dh    dr   tv sp ne ah    ve pa                    pi
1     1  m 32 2.2 3.5    0  5.00  3.0  5  0  0 FALSE  r          conservative
2     2  f 23 2.1 3.5 1200  0.30 15.0  7  5  6 FALSE  d               liberal
3     3  f 27 3.3 3.0 1300  1.50  0.0  4  3  0 FALSE  d               liberal
4     4  f 35 3.5 3.2 1500  8.00  5.0  5  6  3 FALSE  i              moderate
5     5  m 23 3.1 3.5 1600 10.00  6.0  6  3  0 FALSE  i          very liberal
6     6  m 39 3.5 3.5  350  3.00  4.0  5  7  0 FALSE  d               liberal
7     7  m 24 3.6 3.7    0  0.20  5.0 12  4  2 FALSE  i               liberal
8     8  f 31 3.0 3.0 5000  1.50  5.0  3  3  1 FALSE  i               liberal
9     9  m 34 3.0 3.0 5000  2.00  7.0  5  3  0 FALSE  i          very liberal
10   10  m 28 4.0 3.1  900  2.00  1.0  1  2  1 FALSE  i      slightly liberal
11   11  m 23 2.3 2.6  253  1.50 10.0 15  1  1 FALSE  r slightly conservative
12   12  f 27 3.5 3.6  190  3.00 14.0  3  7  0 FALSE  d               liberal
13   13  m 36 3.3 3.5  245  1.50  6.0 15 12  5 FALSE  d          very liberal
14   14  m 28 3.2 3.2  500  6.00  3.0 10  1  2 FALSE  i              moderate
15   15  f 28 3.0 3.5 3500  1.00  4.0  3  1  0 FALSE  d          very liberal
16   16  f 25 3.8 3.3  210 10.00  7.0  6  1  0 FALSE  i               liberal
17   17  f 41 4.0 3.0 1000 15.00  6.0  7  3 10 FALSE  i      slightly liberal
18   18  m 50 3.8 3.8    0  3.00  5.0  9  6 10 FALSE  d               liberal
19   19  m 71 4.0 3.5 5000  3.00  6.0 12  2  2 FALSE  i               liberal
20   20  f 28 3.0 3.8  120  1.00 25.0  0  0  2 FALSE  d          very liberal
21   21  f 26 3.7 3.7 8000  8.00  4.0  4  4  1 FALSE  i              moderate
22   22  f 27 4.0 3.7    2  2.50  4.0  2  7  0 FALSE  i               liberal
23   23  m 31 2.7 3.5 1700  5.00  7.0  7  2  0 FALSE  r     very conservative
24   24  f 23 3.7 3.7    2  2.00  7.0  4  2  0 FALSE  i              moderate
25   25  m 23 3.2 3.8  450  4.00  0.0  7  7  3 FALSE  i          very liberal
26   26  f 44 3.0 3.0    0  2.00  2.0  3  2  3 FALSE  i      slightly liberal
27   27  m 26 3.7 3.0 1000  3.00  8.0  2  7  0 FALSE  d               liberal
28   28  f 31 3.7 3.8  850 10.00 10.0  3  7  0 FALSE  r slightly conservative
29   29  m 24 3.3 3.1  420  2.00 10.0  6  5  0 FALSE  d              moderate
30   30  f 26 3.3 3.3 1200  0.75 10.0  0  3  0 FALSE  r               liberal
31   31  m 26 3.3 3.5 1000  1.50  0.0  3  3  3 FALSE  d               liberal
32   32  f 32 3.5 3.9  150 12.00 10.0  2  0  0 FALSE  d               liberal
33   33  m 26 3.4 3.4 2000  1.50  2.0  7 14  0 FALSE  d               liberal
34   34  f 22 3.2 2.8  316  2.00 10.0  3  5  2 FALSE  i               liberal
35   35  f 24 3.5 3.9  900  1.75  8.0  0  0  1 FALSE  d          very liberal
36   36  m 24 3.6 3.3  250  2.00  4.0  6  3  1 FALSE  r slightly conservative
37   37  m 23 3.8 3.7  180  0.50 10.0  5  7  0 FALSE  i               liberal
38   38  m 33 3.4 3.4 6000  1.50  8.0  5  6  2 FALSE  i               liberal
39   39  m 23 2.8 3.2  950  2.00 37.0 10  5  0 FALSE  r slightly conservative
40   40  m 31 3.8 3.5 1100  0.75  0.5  3  5  2 FALSE  r          conservative
41   41  m 26 3.4 3.4 1300  1.20  0.0  8  2  0 FALSE  i               liberal
42   42  m 28 2.0 3.0  360  0.25 10.0  8  3  0 FALSE  d      slightly liberal
43   43  f 24 3.8 3.9 1800  2.00  2.0  5  4  1 FALSE  r          conservative
44   44  m 23 3.0 3.6  900 15.00 12.0  0  5  0 FALSE  r slightly conservative
45   45  f 25 3.0 4.0 5000  5.00  1.5  0  4  0 FALSE  i              moderate
46   46  f 24 3.0 3.5  300  1.00 10.0  5  5  0 FALSE  d               liberal
47   47  f 27 3.0 3.8 2000 20.00 28.0  7 14  2 FALSE  r      slightly liberal
48   48  m 24 3.3 3.8  630  1.30  2.0  3  5  0 FALSE  r     very conservative
49   49  f 26 3.8 4.0 1200  1.00  0.0  4  3  1 FALSE  d               liberal
50   50  f 27 3.0 4.0  580  2.00  5.0 15  1  2 FALSE  d          very liberal
51   51  m 32 3.0 3.0 2000  5.00  5.0  5  2  1 FALSE  r slightly conservative
52   52  f 41 4.0 4.0    0  8.00  8.0  4  2  2 FALSE  r              moderate
53   53  f 29 3.0 3.9  300  3.70  2.0  5  1 11 FALSE  d               liberal
54   54  f 50 3.5 3.8    6  6.00  7.0  3  7  0 FALSE  d               liberal
55   55  f 22 3.4 3.7   80  7.00 10.0  1  2  2 FALSE  i               liberal
56   56  f 23 3.6 3.2  375  1.50  5.0 10  5  0 FALSE  r          conservative
57   57  m 26 3.5 3.6 2000  0.30 16.0  8  3  0 FALSE  d              moderate
58   58  m 30 3.0 3.0    1  1.10  1.0  4  3  0 FALSE  i      slightly liberal
59   59  f 23 3.0 3.0  112  0.50 15.0  3  3  0 FALSE  i              moderate
60   60  f 22 3.4 3.0  650  4.00  8.0 16  7  1 FALSE  i              moderate
             re    ab    aa    ld
1    most weeks FALSE FALSE FALSE
2  occasionally FALSE FALSE    NA
3    most weeks FALSE FALSE    NA
4  occasionally FALSE FALSE FALSE
5         never FALSE FALSE FALSE
6  occasionally FALSE FALSE    NA
7  occasionally FALSE FALSE FALSE
8  occasionally FALSE FALSE FALSE
9  occasionally FALSE FALSE    NA
10        never FALSE FALSE FALSE
11 occasionally FALSE FALSE FALSE
12 occasionally FALSE FALSE    NA
13 occasionally FALSE FALSE FALSE
14 occasionally FALSE FALSE FALSE
15        never FALSE FALSE FALSE
16   every week FALSE FALSE FALSE
17   every week FALSE    NA FALSE
18        never FALSE FALSE FALSE
19        never FALSE FALSE FALSE
20 occasionally FALSE FALSE FALSE
21 occasionally FALSE FALSE FALSE
22 occasionally FALSE FALSE FALSE
23   every week FALSE FALSE FALSE
24        never FALSE FALSE FALSE
25        never FALSE FALSE FALSE
26   most weeks FALSE FALSE FALSE
27 occasionally FALSE FALSE    NA
28   most weeks FALSE FALSE FALSE
29 occasionally FALSE FALSE    NA
30 occasionally FALSE FALSE    NA
31 occasionally FALSE FALSE FALSE
32 occasionally FALSE FALSE FALSE
33        never FALSE FALSE FALSE
34 occasionally FALSE FALSE    NA
35 occasionally FALSE FALSE    NA
36   every week FALSE FALSE FALSE
37        never FALSE FALSE    NA
38        never FALSE FALSE FALSE
39   most weeks FALSE FALSE FALSE
40   most weeks FALSE FALSE    NA
41 occasionally FALSE FALSE FALSE
42        never FALSE FALSE    NA
43   every week FALSE FALSE FALSE
44        never FALSE FALSE FALSE
45 occasionally FALSE FALSE FALSE
46        never FALSE FALSE FALSE
47 occasionally FALSE FALSE FALSE
48   every week FALSE FALSE FALSE
49        never FALSE FALSE FALSE
50 occasionally FALSE FALSE FALSE
51   every week FALSE FALSE FALSE
52 occasionally FALSE FALSE FALSE
53 occasionally FALSE FALSE FALSE
54 occasionally FALSE FALSE    NA
55        never FALSE FALSE    NA
56   every week FALSE FALSE FALSE
57 occasionally FALSE FALSE    NA
58   every week FALSE FALSE FALSE
59   most weeks FALSE FALSE FALSE
60 occasionally FALSE FALSE FALSE

lm(pi ~ re, data=student.survey)


Call:
lm(formula = pi ~ re, data = student.survey)

Coefficients:
(Intercept)         re.L         re.Q         re.C  
     3.5253       2.1864       0.1049      -0.6958

lm(formula= hi ~ tv, data=student.survey)


Call:
lm(formula = hi ~ tv, data = student.survey)

Coefficients:
(Intercept)           tv  
    3.44135     -0.01831

Political Affiliation and Religiosity: I have no idea what re.Q re.L and re.C is. Both categorical variables take on more than three possible values so I am guessing I have the wrong code.

TV and GPA: For every +1 hr spend watching tv per week, gpa decreases by 0.018. For a student that watches no tv in the week, their predicted gpa is 3.44.