Rows: 60
Columns: 18
$ subj <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19…
$ ge <fct> m, f, f, f, m, m, m, f, m, m, m, f, m, m, f, f, f, m, m, f, f, f,…
$ ag <int> 32, 23, 27, 35, 23, 39, 24, 31, 34, 28, 23, 27, 36, 28, 28, 25, 4…
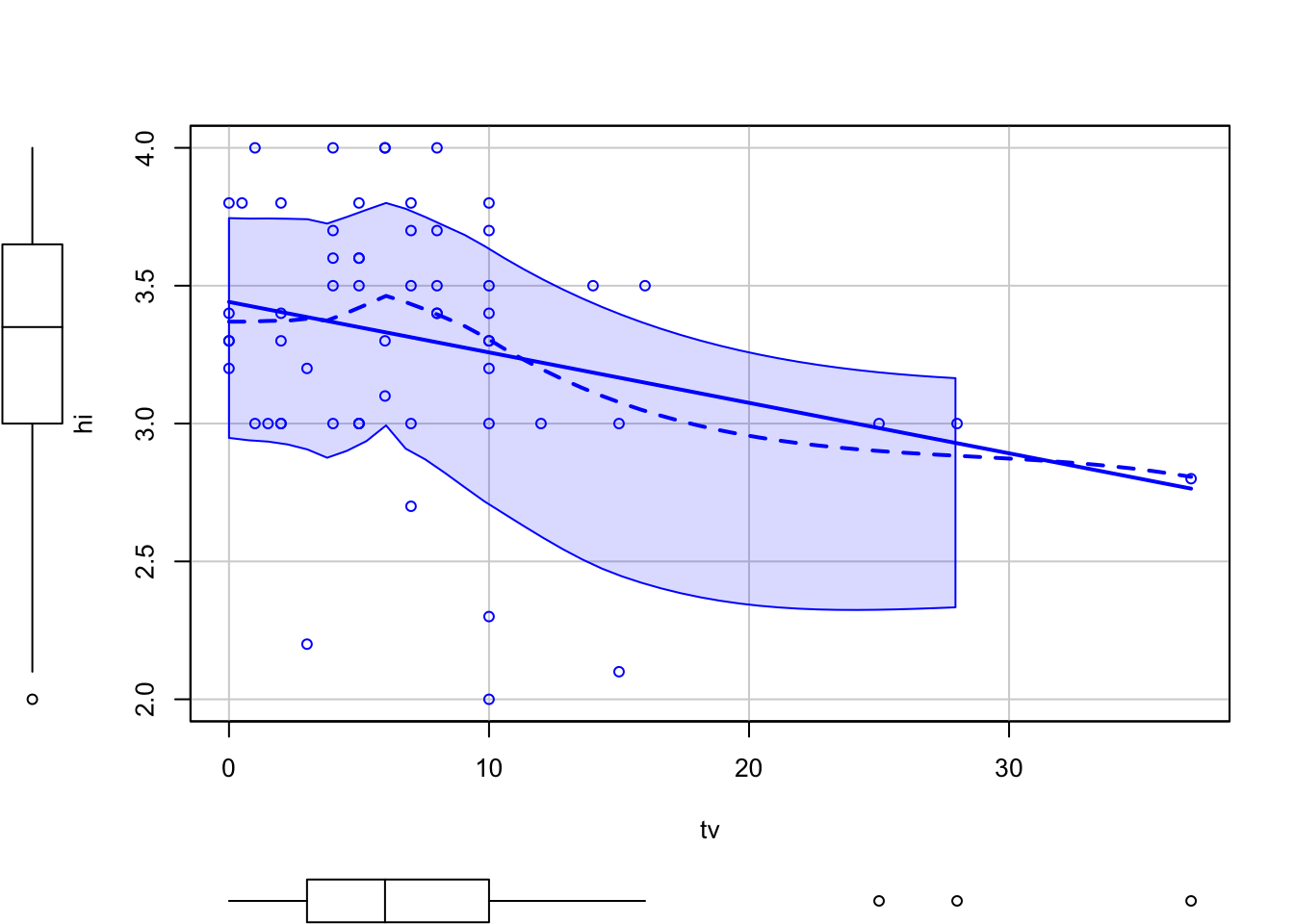
$ hi <dbl> 2.2, 2.1, 3.3, 3.5, 3.1, 3.5, 3.6, 3.0, 3.0, 4.0, 2.3, 3.5, 3.3, …
$ co <dbl> 3.5, 3.5, 3.0, 3.2, 3.5, 3.5, 3.7, 3.0, 3.0, 3.1, 2.6, 3.6, 3.5, …
$ dh <int> 0, 1200, 1300, 1500, 1600, 350, 0, 5000, 5000, 900, 253, 190, 245…
$ dr <dbl> 5.0, 0.3, 1.5, 8.0, 10.0, 3.0, 0.2, 1.5, 2.0, 2.0, 1.5, 3.0, 1.5,…
$ tv <dbl> 3, 15, 0, 5, 6, 4, 5, 5, 7, 1, 10, 14, 6, 3, 4, 7, 6, 5, 6, 25, 4…
$ sp <int> 5, 7, 4, 5, 6, 5, 12, 3, 5, 1, 15, 3, 15, 10, 3, 6, 7, 9, 12, 0, …
$ ne <int> 0, 5, 3, 6, 3, 7, 4, 3, 3, 2, 1, 7, 12, 1, 1, 1, 3, 6, 2, 0, 4, 7…
$ ah <int> 0, 6, 0, 3, 0, 0, 2, 1, 0, 1, 1, 0, 5, 2, 0, 0, 10, 10, 2, 2, 1, …
$ ve <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FA…
$ pa <fct> r, d, d, i, i, d, i, i, i, i, r, d, d, i, d, i, i, d, i, d, i, i,…
$ pi <ord> conservative, liberal, liberal, moderate, very liberal, liberal, …
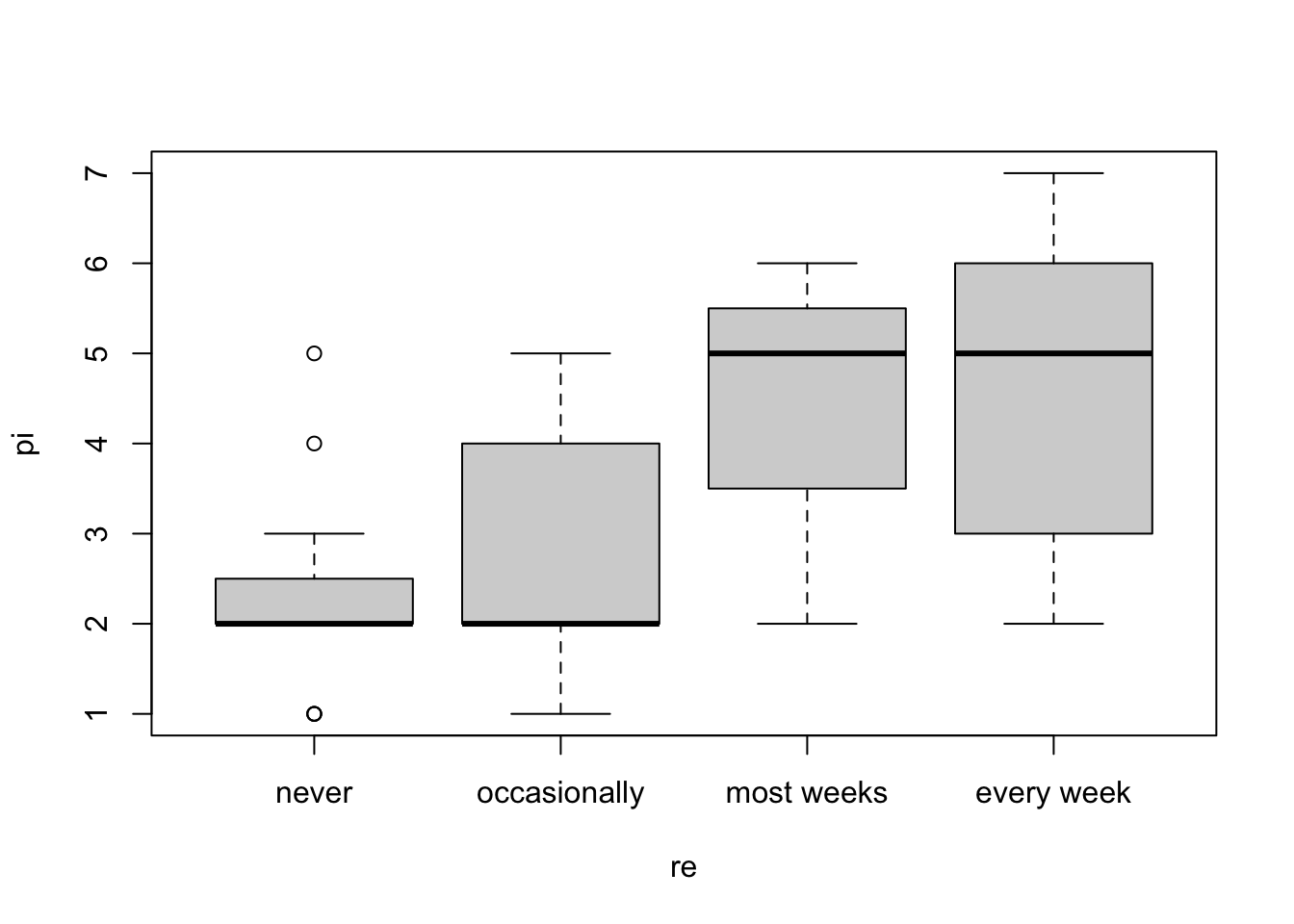
$ re <ord> most weeks, occasionally, most weeks, occasionally, never, occasi…
$ ab <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FA…
$ aa <lgl> FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FALSE, FA…
$ ld <lgl> FALSE, NA, NA, FALSE, FALSE, NA, FALSE, FALSE, NA, FALSE, FALSE, …