library(tidyverse)
library(alr4)
library(smss)
library(interactions)
knitr::opts_chunk$set(echo = TRUE, warning = FALSE, message = FALSE)Homework 4
Qn 1A
# predicted price.
yhat <- -10536 + 53.8*1240 + 2.84*18000
# residual.
145000-yhat[1] 37704The model under-predicts by $37,704.
Qn 1B
It is predicted to increase by ~$53.80. This is because the effects of x1 and x2 on y are independent of one another, and there is no interaction between them.
Qn 1C
53.8/2.84[1] 18.94366It would need to increase by ~19x.
Qn 2A
# load dataset.
data(salary)
# run model.
summary(lm(salary ~ sex, salary))
Call:
lm(formula = salary ~ sex, data = salary)
Residuals:
Min 1Q Median 3Q Max
-8602.8 -4296.6 -100.8 3513.1 16687.9
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24697 938 26.330 <2e-16 ***
sexFemale -3340 1808 -1.847 0.0706 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5782 on 50 degrees of freedom
Multiple R-squared: 0.0639, Adjusted R-squared: 0.04518
F-statistic: 3.413 on 1 and 50 DF, p-value: 0.0706The mean salary for men and women does not differ, p = 0.07 (i.e., it is the same).
Qn 2B
# run model.
model2B <- lm(salary ~ ., salary)
summary(model2B)
Call:
lm(formula = salary ~ ., data = salary)
Residuals:
Min 1Q Median 3Q Max
-4045.2 -1094.7 -361.5 813.2 9193.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15746.05 800.18 19.678 < 2e-16 ***
degreePhD 1388.61 1018.75 1.363 0.180
rankAssoc 5292.36 1145.40 4.621 3.22e-05 ***
rankProf 11118.76 1351.77 8.225 1.62e-10 ***
sexFemale 1166.37 925.57 1.260 0.214
year 476.31 94.91 5.018 8.65e-06 ***
ysdeg -124.57 77.49 -1.608 0.115
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2398 on 45 degrees of freedom
Multiple R-squared: 0.855, Adjusted R-squared: 0.8357
F-statistic: 44.24 on 6 and 45 DF, p-value: < 2.2e-16# get confidence interval.
confint(model2B) 2.5 % 97.5 %
(Intercept) 14134.4059 17357.68946
degreePhD -663.2482 3440.47485
rankAssoc 2985.4107 7599.31080
rankProf 8396.1546 13841.37340
sexFemale -697.8183 3030.56452
year 285.1433 667.47476
ysdeg -280.6397 31.49105Sex is still not a significant predictor of salary. The 95% CI for difference in salary between males and females is approx. -698 to 3031.
Qn 2C
rank and year are significant predictors of salary, while all others were not.
Both rank and year positively predict salary: Associate Professors and full Professors were likely to earn quite a bit more than Assistant Professors, while professors with more years in their current rank also earned more.
Looking at the magnitude of the coefficients, rank has a greater impact on salary than year does.
Qn 2D
# change baseline category.
salary$rank <- relevel(salary$rank, ref = 'Assoc')
# re-run model.
model2D <- lm(salary ~ ., salary)
summary(model2D)
Call:
lm(formula = salary ~ ., data = salary)
Residuals:
Min 1Q Median 3Q Max
-4045.2 -1094.7 -361.5 813.2 9193.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 21038.41 1109.12 18.969 < 2e-16 ***
degreePhD 1388.61 1018.75 1.363 0.180
rankAsst -5292.36 1145.40 -4.621 3.22e-05 ***
rankProf 5826.40 1012.93 5.752 7.28e-07 ***
sexFemale 1166.37 925.57 1.260 0.214
year 476.31 94.91 5.018 8.65e-06 ***
ysdeg -124.57 77.49 -1.608 0.115
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2398 on 45 degrees of freedom
Multiple R-squared: 0.855, Adjusted R-squared: 0.8357
F-statistic: 44.24 on 6 and 45 DF, p-value: < 2.2e-16We can see that rank now both negatively and positively predicts salary. Specifically, Assistant Professors earn less than Associate Professors do, at the same magnitude that was observed in model1 (approx. ~$5292).
Qn 2E
model2E <- lm(salary ~ . - rank, salary)
summary(model2E)
Call:
lm(formula = salary ~ . - rank, data = salary)
Residuals:
Min 1Q Median 3Q Max
-8146.9 -2186.9 -491.5 2279.1 11186.6
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17183.57 1147.94 14.969 < 2e-16 ***
degreePhD -3299.35 1302.52 -2.533 0.014704 *
sexFemale -1286.54 1313.09 -0.980 0.332209
year 351.97 142.48 2.470 0.017185 *
ysdeg 339.40 80.62 4.210 0.000114 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3744 on 47 degrees of freedom
Multiple R-squared: 0.6312, Adjusted R-squared: 0.5998
F-statistic: 20.11 on 4 and 47 DF, p-value: 1.048e-09Excluding rank, both adjusted R2 and the overall F-statistic drop. degree and ysdeg are now significant as well. Curiously, those with a PhD earn less than those with an MS. As years since highest degree increases, so does salary.
Qn 2F
# create new variable.
salary <- mutate(salary, HireTime = case_when(ysdeg <= 15 ~ "1", ysdeg > 15 ~ "0"))
salary$HireTime <- as.numeric(salary$HireTime)
# run correlation matrix to check for multicollinearity. it's important to do so especially because HireTime is derived from ysdeg, so we would expect them to be highly correlated.
subset <- salary %>% select(year, ysdeg, HireTime)
matrix <- cor(subset, use="complete.obs")I would remove ysdeg from the regression model since it is highly correlated with HireTime, r = 0.84.
model2F <- lm(salary ~ . - ysdeg, salary)
summary(model2F)
Call:
lm(formula = salary ~ . - ysdeg, data = salary)
Residuals:
Min 1Q Median 3Q Max
-3403.3 -1387.0 -167.0 528.2 9233.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18301.04 1301.36 14.063 < 2e-16 ***
degreePhD 818.93 797.48 1.027 0.3100
rankAsst -4972.66 997.17 -4.987 9.61e-06 ***
rankProf 6124.28 1028.58 5.954 3.65e-07 ***
sexFemale 907.14 840.54 1.079 0.2862
year 434.85 78.89 5.512 1.65e-06 ***
HireTime 2163.46 1072.04 2.018 0.0496 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2362 on 45 degrees of freedom
Multiple R-squared: 0.8594, Adjusted R-squared: 0.8407
F-statistic: 45.86 on 6 and 45 DF, p-value: < 2.2e-16Yes, those hired by the new Dean are making more, p = .05.
Qn 3A
# load dataset.
data(house.selling.price)
# run model.
model3A <- lm(Price ~ Size + New, house.selling.price)
summary(model3A)
Call:
lm(formula = Price ~ Size + New, data = house.selling.price)
Residuals:
Min 1Q Median 3Q Max
-205102 -34374 -5778 18929 163866
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -40230.867 14696.140 -2.738 0.00737 **
Size 116.132 8.795 13.204 < 2e-16 ***
New 57736.283 18653.041 3.095 0.00257 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 53880 on 97 degrees of freedom
Multiple R-squared: 0.7226, Adjusted R-squared: 0.7169
F-statistic: 126.3 on 2 and 97 DF, p-value: < 2.2e-16Both Size and New significantly positively predict selling price. As each predictor goes up by 1 unit, selling price rises by $116 and $57,736 respectively.
Qn 3B
# new homes.
new <- house.selling.price %>% filter(New == 1)
model3B1 <- lm(Price ~ Size, new)
summary(model3B1)
Call:
lm(formula = Price ~ Size, data = new)
Residuals:
Min 1Q Median 3Q Max
-78606 -16092 -987 20068 76140
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -100755.31 42513.73 -2.370 0.0419 *
Size 166.35 17.09 9.735 4.47e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 45500 on 9 degrees of freedom
Multiple R-squared: 0.9133, Adjusted R-squared: 0.9036
F-statistic: 94.76 on 1 and 9 DF, p-value: 4.474e-06# old homes.
old <- house.selling.price %>% filter(New == 0)
model3B2 <- lm(Price ~ Size, old)
summary(model3B2)
Call:
lm(formula = Price ~ Size, data = old)
Residuals:
Min 1Q Median 3Q Max
-175748 -29155 -7297 14159 192519
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -22227.808 15708.186 -1.415 0.161
Size 104.438 9.538 10.950 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 52620 on 87 degrees of freedom
Multiple R-squared: 0.5795, Adjusted R-squared: 0.5747
F-statistic: 119.9 on 1 and 87 DF, p-value: < 2.2e-16Size significantly positively predicts price for both new and old houses, but by a greater magnitude for new houses:
New: E(Price) = 166*Size - 100,755
- Adjusted R2 for the model is also much higher (0.90 vs. 0.57).
Old: E(Price) = 104*Size - 22,228
Qn 3C
New: E(Price) = 166*3000 - 100,755 = $397,245
Old: E(Price) = 104*3000 - 22,228 = $289,772
Qn 3D
model3D <- lm(Price ~ Size*New, house.selling.price)
summary(model3D)
Call:
lm(formula = Price ~ Size * New, data = house.selling.price)
Residuals:
Min 1Q Median 3Q Max
-175748 -28979 -6260 14693 192519
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -22227.808 15521.110 -1.432 0.15536
Size 104.438 9.424 11.082 < 2e-16 ***
New -78527.502 51007.642 -1.540 0.12697
Size:New 61.916 21.686 2.855 0.00527 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 52000 on 96 degrees of freedom
Multiple R-squared: 0.7443, Adjusted R-squared: 0.7363
F-statistic: 93.15 on 3 and 96 DF, p-value: < 2.2e-16interact_plot(model3D, pred = Size, modx = New)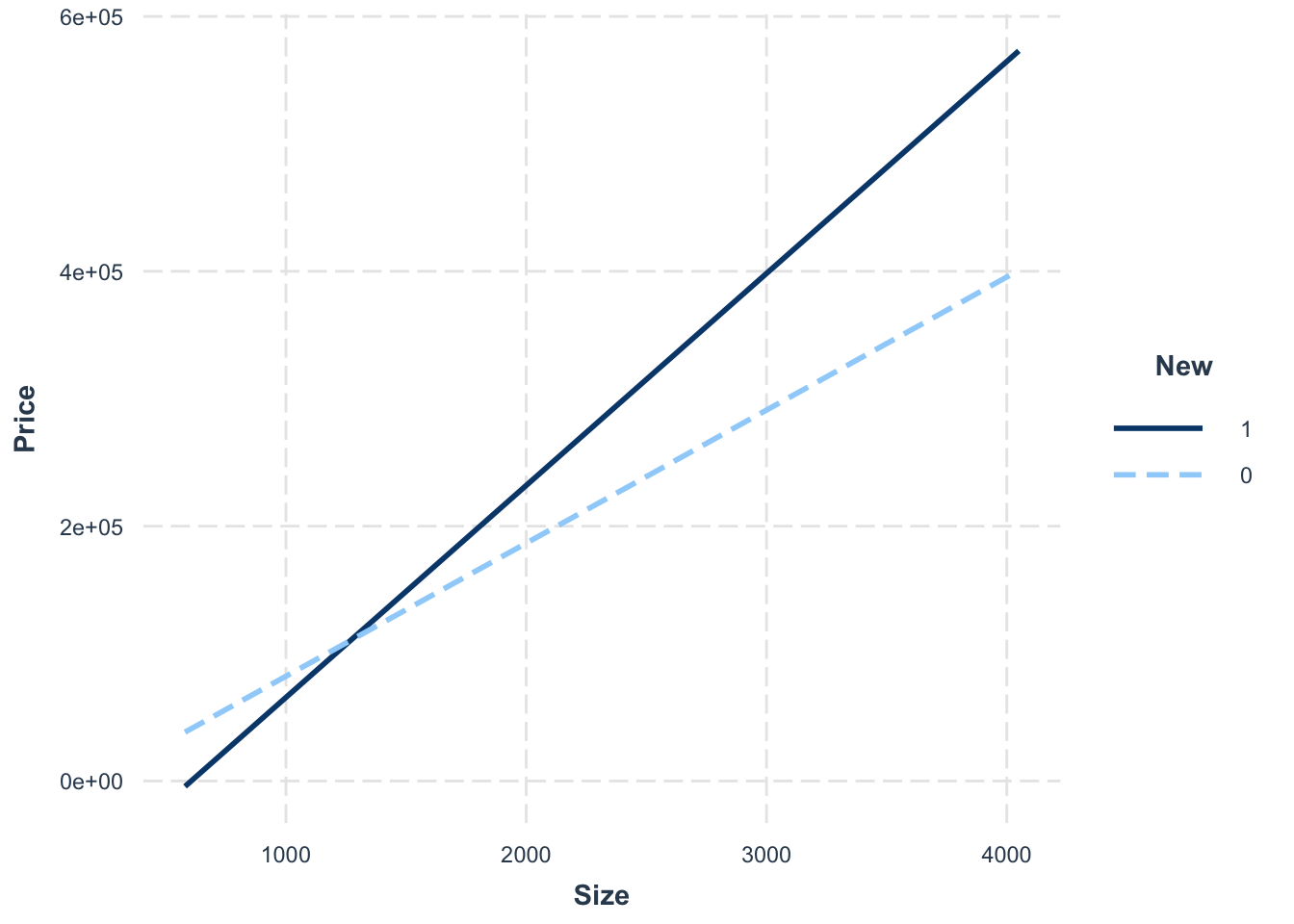
Size and New positively interact to affect Price, such that New amplifies the positive relationship between Size and Price.
Qn 3E
Referring to model3D above:
New: -22,228 + 104*Size - 78,528 + 62*Size = 166*Size - 100,756
Old: 104*Size - 22,228
Qn 3F
New: 166*3000 -100,756 = $397,244
Old: 104*3000 - 22,228 = $289,772
Qn 3G
New: 166*1500 - 100,756 = $148,244
Old: 104*1500 - 22,228 = $133,772
As size of home goes up, the difference in predicted selling prices between old and new homes becomes larger.
Qn 3H
Questions 3F and 3G demonstrate that size affects the relationship between new and price, which reveals some type of dependency between the predictors. Hence, the model with interaction represents the relationships between size, new and price better.