Homework 4

hw4

Homework 4

Author

Steve O’Neill

Published

November 16, 2022

Code

library(alr4)

Loading required package: car

Loading required package: carData

Loading required package: effects

lattice theme set by effectsTheme()
See ?effectsTheme for details.

Code

library(smss)

Question 1

For recent data in Jacksonville, Florida, on y = selling price of home (in dollars), x1 = size of home (in square feet), and x2 = lot size (in square feet), the prediction equation is ŷ = −10,536 + 53.8x1 + 2.84x2

A. A particular home of 1240 square feet on a lot of 18,000 square feet sold for $145,000. Find the predicted selling price and the residual, and interpret.

Code

home_size <- 1240
lot_size <- 18000

y = -10536 + (53.8 * home_size) + (2.84 * lot_size)
y

[1] 107296

Code

145000 - y

[1] 37704

The predicted selling price of the home is $107,296. The residual is $37704, which means the model under-predicted.

B. Holding home size fixed, each one-square-foot increase in lot size brings a 2.84 increase in dollar value.

C. Holding lot size fixed, each sq. ft. increase in home size results in a $53.8 increase in home price.

Question 2

(Data file: salary in alr4 R package). The data file concerns salary and other characteristics of all faculty in a small Midwestern college collected in the early 1980s for presentation in legal proceedings for which discrimination against women in salary was at issue. All persons in the data hold tenured or tenure track positions; temporary faculty are not included. The variables include degree, a factor with levels PhD and MS; rank, a factor with levels Asst, Assoc, and Prof; sex, a factor with levels Male and Female; Year, years in current rank; ysdeg, years since highest degree, and salary, academic year salary in dollars.

Code

data(salary)
salary

    degree  rank    sex year ysdeg salary
1  Masters  Prof   Male   25    35  36350
2  Masters  Prof   Male   13    22  35350
3  Masters  Prof   Male   10    23  28200
4  Masters  Prof Female    7    27  26775
5      PhD  Prof   Male   19    30  33696
6  Masters  Prof   Male   16    21  28516
7      PhD  Prof Female    0    32  24900
8  Masters  Prof   Male   16    18  31909
9      PhD  Prof   Male   13    30  31850
10     PhD  Prof   Male   13    31  32850
11 Masters  Prof   Male   12    22  27025
12 Masters Assoc   Male   15    19  24750
13 Masters  Prof   Male    9    17  28200
14     PhD Assoc   Male    9    27  23712
15 Masters  Prof   Male    9    24  25748
16 Masters  Prof   Male    7    15  29342
17 Masters  Prof   Male   13    20  31114
18     PhD Assoc   Male   11    14  24742
19     PhD Assoc   Male   10    15  22906
20     PhD  Prof   Male    6    21  24450
21     PhD  Asst   Male   16    23  19175
22     PhD Assoc   Male    8    31  20525
23 Masters  Prof   Male    7    13  27959
24 Masters  Prof Female    8    24  38045
25 Masters Assoc   Male    9    12  24832
26 Masters  Prof   Male    5    18  25400
27 Masters Assoc   Male   11    14  24800
28 Masters  Prof Female    5    16  25500
29     PhD Assoc   Male    3     7  26182
30     PhD Assoc   Male    3    17  23725
31     PhD  Asst Female   10    15  21600
32     PhD Assoc   Male   11    31  23300
33     PhD  Asst   Male    9    14  23713
34     PhD Assoc Female    4    33  20690
35     PhD Assoc Female    6    29  22450
36 Masters Assoc   Male    1     9  20850
37 Masters  Asst Female    8    14  18304
38 Masters  Asst   Male    4     4  17095
39 Masters  Asst   Male    4     5  16700
40 Masters  Asst   Male    4     4  17600
41 Masters  Asst   Male    3     4  18075
42     PhD  Asst   Male    3    11  18000
43 Masters Assoc   Male    0     7  20999
44 Masters  Asst Female    3     3  17250
45 Masters  Asst   Male    2     3  16500
46 Masters  Asst   Male    2     1  16094
47 Masters  Asst Female    2     6  16150
48 Masters  Asst Female    2     2  15350
49 Masters  Asst   Male    1     1  16244
50 Masters  Asst Female    1     1  16686
51 Masters  Asst Female    1     1  15000
52 Masters  Asst Female    0     2  20300

Test the hypothesis that the mean salary for men and women is the same, without regard to any other variable but sex. Explain your findings.

Code

summary(lm(salary$salary ~ salary$sex))


Call:
lm(formula = salary$salary ~ salary$sex)

Residuals:
    Min      1Q  Median      3Q     Max 
-8602.8 -4296.6  -100.8  3513.1 16687.9 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)         24697        938  26.330   <2e-16 ***
salary$sexFemale    -3340       1808  -1.847   0.0706 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5782 on 50 degrees of freedom
Multiple R-squared:  0.0639,    Adjusted R-squared:  0.04518 
F-statistic: 3.413 on 1 and 50 DF,  p-value: 0.0706

The hypothesis that mean salary for men and women is the same without regard to any other variable but sex is confirmed. Normally, I would expect this to be phrased as the null hypothesis. But to answer the specific wording of this question, the hypothesis (of ‘sameness’) is confirmed and the null hypothesis (of difference) is rejected.

Run a multiple linear regression with salary as the outcome variable and everything else as predictors, including sex. Assuming no interactions between sex and the other predictors, obtain a 95% confidence interval for the difference in salary between males and females.

Code

summary(lm(salary ~ ., data = salary))


Call:
lm(formula = salary ~ ., data = salary)

Residuals:
    Min      1Q  Median      3Q     Max 
-4045.2 -1094.7  -361.5   813.2  9193.1 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 15746.05     800.18  19.678  < 2e-16 ***
degreePhD    1388.61    1018.75   1.363    0.180    
rankAssoc    5292.36    1145.40   4.621 3.22e-05 ***
rankProf    11118.76    1351.77   8.225 1.62e-10 ***
sexFemale    1166.37     925.57   1.260    0.214    
year          476.31      94.91   5.018 8.65e-06 ***
ysdeg        -124.57      77.49  -1.608    0.115    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2398 on 45 degrees of freedom
Multiple R-squared:  0.855, Adjusted R-squared:  0.8357 
F-statistic: 44.24 on 6 and 45 DF,  p-value: < 2.2e-16

Code

moe = qt(.975, df=45) * 925.57 #aka standard error
upper<- 1166.37 + moe #1166.37 is the coefficient of sexFemale
lower<- 1166.37 - moe 
upper

[1] 3030.564

Code

lower

[1] -697.8237

The confidence interval is (-697.8237, 3030.564)

Here are the findings from earlier:

Interpret your finding for each predictor variable; discuss (a) statistical significance, (b) interpretation of the coefficient / slope in relation to the outcome variable and other variables

The standout variables are rank and year. Being a full professor has double the effect on salary as an associate, and the p-value is also much smaller. Year has a smaller yet significant effect. Asst is missing because it is the baseline category.

Years since highest degree earned is not statistically significant, nor seems to be sex (in this dataset, with these observations).

Change the baseline category for the rank variable. Interpret the coefficients related to rank again.

Code

salary$rank <- relevel(salary$rank, ref = "Assoc")
summary(lm(salary ~ ., data = salary))


Call:
lm(formula = salary ~ ., data = salary)

Residuals:
    Min      1Q  Median      3Q     Max 
-4045.2 -1094.7  -361.5   813.2  9193.1 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 21038.41    1109.12  18.969  < 2e-16 ***
degreePhD    1388.61    1018.75   1.363    0.180    
rankAsst    -5292.36    1145.40  -4.621 3.22e-05 ***
rankProf     5826.40    1012.93   5.752 7.28e-07 ***
sexFemale    1166.37     925.57   1.260    0.214    
year          476.31      94.91   5.018 8.65e-06 ***
ysdeg        -124.57      77.49  -1.608    0.115    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2398 on 45 degrees of freedom
Multiple R-squared:  0.855, Adjusted R-squared:  0.8357 
F-statistic: 44.24 on 6 and 45 DF,  p-value: < 2.2e-16

With rankAssoc excluded and rankAsst included, now we also see that being an assistant professor is negatively correlated with salary - this makes sense considering basic intuition.

Finkelstein (1980), in a discussion of the use of regression in discrimination cases, wrote, “[a] variable may reflect a position or status bestowed by the employer, in which case if there is discrimination in the award of the position or status, the variable may be ‘tainted.’” Thus, for example, if discrimination is at work in promotion of faculty to higher ranks, using rank to adjust salaries before comparing the sexes may not be acceptable to the courts.

Exclude the variable rank, refit, and summarize how your findings changed, if they did.

Code

summary(lm(salary ~ . - rank, data = salary))


Call:
lm(formula = salary ~ . - rank, data = salary)

Residuals:
    Min      1Q  Median      3Q     Max 
-8146.9 -2186.9  -491.5  2279.1 11186.6 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 17183.57    1147.94  14.969  < 2e-16 ***
degreePhD   -3299.35    1302.52  -2.533 0.014704 *  
sexFemale   -1286.54    1313.09  -0.980 0.332209    
year          351.97     142.48   2.470 0.017185 *  
ysdeg         339.40      80.62   4.210 0.000114 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3744 on 47 degrees of freedom
Multiple R-squared:  0.6312,    Adjusted R-squared:  0.5998 
F-statistic: 20.11 on 4 and 47 DF,  p-value: 1.048e-09

With rank removed entirely, years since highest degree earned becomes the most significant variable, with PhD and years of service also being significant.

Everyone in this dataset was hired the year they earned their highest degree. It is also known that a new Dean was appointed 15 years ago, and everyone in the dataset who earned their highest degree 15 years ago or less than that has been hired by the new Dean. Some people have argued that the new Dean has been making offers that are a lot more generous to newly hired faculty than the previous one and that this might explain some of the variation in Salary.

Create a new variable that would allow you to test this hypothesis and run another multiple regression model to test this. Select variables carefully to make sure there is no multicollinearity. Explain why multicollinearity would be a concern in this case and how you avoided it. Do you find support for the hypothesis that the people hired by the new Dean are making higher than those that were not?

Code

salary$dean_old <- ifelse(salary$year >=15, 1, 0)
head(salary[c('dean_old', 'year')], n = 10)

   dean_old year
1         1   25
2         0   13
3         0   10
4         0    7
5         1   19
6         1   16
7         0    0
8         1   16
9         0   13
10        0   13

For the new linear model, I am excluding years of service and only including years since highest degree attained. Since dean_old is derived from year, this avoids multicolinearity:

Code

summary(lm(salary ~ . -year, data = salary))


Call:
lm(formula = salary ~ . - year, data = salary)

Residuals:
    Min      1Q  Median      3Q     Max 
-5076.5 -1468.1  -569.6  1382.1  9444.4 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 21735.66    1362.56  15.952  < 2e-16 ***
degreePhD     436.19    1217.06   0.358  0.72172    
rankAsst    -4265.73    1372.22  -3.109  0.00325 ** 
rankProf     6153.34    1225.02   5.023 8.52e-06 ***
sexFemale    -661.30    1013.29  -0.653  0.51732    
ysdeg          57.20      80.92   0.707  0.48324    
dean_old     2401.72    1415.86   1.696  0.09674 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2904 on 45 degrees of freedom
Multiple R-squared:  0.7875,    Adjusted R-squared:  0.7592 
F-statistic: 27.79 on 6 and 45 DF,  p-value: 1.34e-13

After including the new “dean” variable and removing year, I don’t find a significant difference in the salaries of professors hiring the two new deans - in other words, the null hypothesis fails to be rejected. It would be significant at a 90% confidence level, but we went in with a 5% significance level

It could be argued that year, representing years of service to the university, is colinear with ysdeg, years since highest degree earned. Both of them are a function of time and represent the career-stage of a professor. However, I think professors often come in from different universities so they are not necessarily correlated. I could really see it both ways. If that variable is also removed, the dean_old variable becomes significant at the 5% confidence level.

Code

library(smss)
data("house.selling.price")
house.selling.price

    case Taxes Beds Baths New  Price Size
1      1  3104    4     2   0 279900 2048
2      2  1173    2     1   0 146500  912
3      3  3076    4     2   0 237700 1654
4      4  1608    3     2   0 200000 2068
5      5  1454    3     3   0 159900 1477
6      6  2997    3     2   1 499900 3153
7      7  4054    3     2   0 265500 1355
8      8  3002    3     2   1 289900 2075
9      9  6627    5     4   0 587000 3990
10    10   320    3     2   0  70000 1160
11    11   630    3     2   0  64500 1220
12    12  1780    3     2   0 167000 1690
13    13  1630    3     2   0 114600 1380
14    14  1530    3     2   0 103000 1590
15    15   930    3     1   0 101000 1050
16    16   590    2     1   0  70000  770
17    17  1050    3     2   0  85000 1410
18    18    20    3     1   0  22500 1060
19    19   870    2     2   0  90000 1300
20    20  1320    3     2   0 133000 1500
21    21  1350    2     1   0  90500  820
22    22  5616    4     3   1 577500 3949
23    23   680    2     1   0 142500 1170
24    24  1840    3     2   0 160000 1500
25    25  3680    4     2   0 240000 2790
26    26  1660    3     1   0  87000 1030
27    27  1620    3     2   0 118600 1250
28    28  3100    3     2   0 140000 1760
29    29  2070    2     3   0 148000 1550
30    30   830    3     2   0  69000 1120
31    31  2260    4     2   0 176000 2000
32    32  1760    3     1   0  86500 1350
33    33  2750    3     2   1 180000 1840
34    34  2020    4     2   0 179000 2510
35    35  4900    3     3   1 338000 3110
36    36  1180    4     2   0 130000 1760
37    37  2150    3     2   0 163000 1710
38    38  1600    2     1   0 125000 1110
39    39  1970    3     2   0 100000 1360
40    40  2060    3     1   0 100000 1250
41    41  1980    3     1   0 100000 1250
42    42  1510    3     2   0 146500 1480
43    43  1710    3     2   0 144900 1520
44    44  1590    3     2   0 183000 2020
45    45  1230    3     2   0  69900 1010
46    46  1510    2     2   0  60000 1640
47    47  1450    2     2   0 127000  940
48    48   970    3     2   0  86000 1580
49    49   150    2     2   0  50000  860
50    50  1470    3     2   0 137000 1420
51    51  1850    3     2   0 121300 1270
52    52   820    2     1   0  81000  980
53    53  2050    4     2   0 188000 2300
54    54   710    3     2   0  85000 1430
55    55  1280    3     2   0 137000 1380
56    56  1360    3     2   0 145000 1240
57    57   830    3     2   0  69000 1120
58    58   800    3     2   0 109300 1120
59    59  1220    3     2   0 131500 1900
60    60  3360    4     3   0 200000 2430
61    61   210    3     2   0  81900 1080
62    62   380    2     1   0  91200 1350
63    63  1920    4     3   0 124500 1720
64    64  4350    3     3   0 225000 4050
65    65  1510    3     2   0 136500 1500
66    66  4154    3     3   0 381000 2581
67    67  1976    3     2   1 250000 2120
68    68  3605    3     3   1 354900 2745
69    69  1400    3     2   0 140000 1520
70    70   790    2     2   0  89900 1280
71    71  1210    3     2   0 137000 1620
72    72  1550    3     2   0 103000 1520
73    73  2800    3     2   0 183000 2030
74    74  2560    3     2   0 140000 1390
75    75  1390    4     2   0 160000 1880
76    76  5443    3     2   0 434000 2891
77    77  2850    2     1   0 130000 1340
78    78  2230    2     2   0 123000  940
79    79    20    2     1   0  21000  580
80    80  1510    4     2   0  85000 1410
81    81   710    3     2   0  69900 1150
82    82  1540    3     2   0 125000 1380
83    83  1780    3     2   1 162600 1470
84    84  2920    2     2   1 156900 1590
85    85  1710    3     2   1 105900 1200
86    86  1880    3     2   0 167500 1920
87    87  1680    3     2   0 151800 2150
88    88  3690    5     3   0 118300 2200
89    89   900    2     2   0  94300  860
90    90   560    3     1   0  93900 1230
91    91  2040    4     2   0 165000 1140
92    92  4390    4     3   1 285000 2650
93    93   690    3     1   0  45000 1060
94    94  2100    3     2   0 124900 1770
95    95  2880    4     2   0 147000 1860
96    96   990    2     2   0 176000 1060
97    97  3030    3     2   0 196500 1730
98    98  1580    3     2   0 132200 1370
99    99  1770    3     2   0  88400 1560
100  100  1430    3     2   0 127200 1340

Code

summary(lm(Price ~ Size + New, data = house.selling.price))


Call:
lm(formula = Price ~ Size + New, data = house.selling.price)

Residuals:
    Min      1Q  Median      3Q     Max 
-205102  -34374   -5778   18929  163866 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -40230.867  14696.140  -2.738  0.00737 ** 
Size           116.132      8.795  13.204  < 2e-16 ***
New          57736.283  18653.041   3.095  0.00257 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 53880 on 97 degrees of freedom
Multiple R-squared:  0.7226,    Adjusted R-squared:  0.7169 
F-statistic: 126.3 on 2 and 97 DF,  p-value: < 2.2e-16

Both size and new are statistically significant variables. The size variable has a much lower p-value, meeting 0.1 % significance level.

An increase in one sq. ft. of size may increase a house’s value by $116.13 if new is held constant. A house being new can affect the price by $57,736.28 with size being held constant.

The prediction equation would be:

Predicted Price = 116.132(Size) + 57736.283(New) -40230.867

Code

summary(lm(Price ~ New, data = house.selling.price))


Call:
lm(formula = Price ~ New, data = house.selling.price)

Residuals:
    Min      1Q  Median      3Q     Max 
-185064  -49042   -9967   22183  448433 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   138567       9504  14.580  < 2e-16 ***
New           152396      28655   5.318 6.61e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 89660 on 98 degrees of freedom
Multiple R-squared:  0.224, Adjusted R-squared:  0.2161 
F-statistic: 28.28 on 1 and 98 DF,  p-value: 6.608e-07

Report and interpret the prediction equation, and form separate equations relating selling price to size for new and for not new homes.

Equations for just size and just newness, respectively, are:

Predicted Price = 126.594(Size) -50926.255

Predicted Price = 152396(New) + 138567

Find the predicted selling price for a home of 3000 square feet that is (i) new, (ii) not new.

Code

new <- 1
notnew <- 0
size <- 3000

(116.132 * size) + (57736.283 * new) -40230.867

[1] 365901.4

Code

(116.132 * size) + (57736.283 * notnew) -40230.867

[1] 308165.1

The predicted selling price of a new vs not new home of 3000 sq/ft is $365901.4 and $308165.1, respectively.

Fit another model, this time with an interaction term allowing interaction between size and new, and report the regression results

Code

fit <- summary(lm(Price ~ Size + New + Size * New, data = house.selling.price))
fit


Call:
lm(formula = Price ~ Size + New + Size * New, data = house.selling.price)

Residuals:
    Min      1Q  Median      3Q     Max 
-175748  -28979   -6260   14693  192519 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -22227.808  15521.110  -1.432  0.15536    
Size           104.438      9.424  11.082  < 2e-16 ***
New         -78527.502  51007.642  -1.540  0.12697    
Size:New        61.916     21.686   2.855  0.00527 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 52000 on 96 degrees of freedom
Multiple R-squared:  0.7443,    Adjusted R-squared:  0.7363 
F-statistic: 93.15 on 3 and 96 DF,  p-value: < 2.2e-16

Report the lines relating the predicted selling price to the size for homes that are (i) new, (ii) not new.

Code

library(ggplot2)

new_labels <- c(
                    `0` = "Not New",
                    `1` = "New"
                    )

ggplot(house.selling.price, aes(x = Size, y = Price)) + 
  geom_point() +
  stat_smooth(method = "lm", col = "red") +
  facet_grid(house.selling.price$New, labeller = as_labeller(new_labels)) + 
  scale_y_continuous(labels=scales::dollar_format())

`geom_smooth()` using formula = 'y ~ x'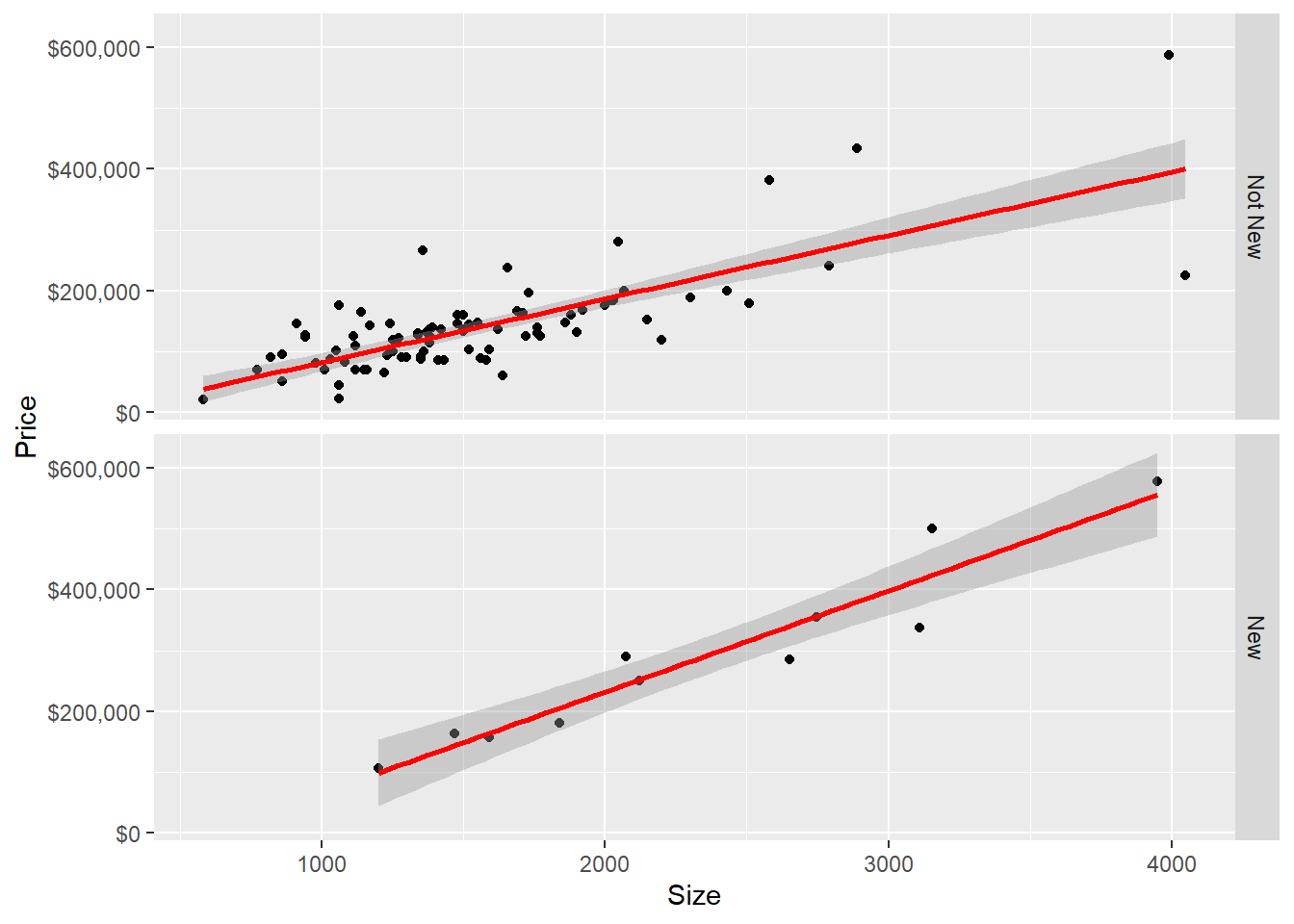

Here is a faceted plot representation of New, re: Size and Price.

Find the predicted selling price for a home of 3000 square feet that is (i) new, (ii) not new.

Code

size <- 3000
size_coef <- 104.438
new_coef <- -78527.502
sizenew_coef <- 61.916

(size_coef * size) + (new_coef * 0) + (sizenew_coef * 0 * 3000) - 22227.808

[1] 291086.2

Code

(size_coef * size) + (new_coef * 1) + (sizenew_coef * 1 * 3000) - 22227.808

[1] 398306.7

The predicted selling price for homes of 3000 sq/ft are, taking into account condition:

Not new: $291086.2 New: $398306.7

Find the predicted selling price for a home of 1500 square feet that is (i) new, (ii) not new. Comparing to (F), explain how the difference in predicted selling prices changes as the size of home increases.

Code

size <- 1500
size_coef <- 104.438
new_coef <- -78527.502
sizenew_coef <- 61.916

(size_coef * size) + (new_coef * 0) + (sizenew_coef * 0 * size) - 22227.808

[1] 134429.2

Code

(size_coef * size) + (new_coef * 1) + (sizenew_coef * 1 * size) - 22227.808

[1] 148775.7

Here, the costs are $134429.2 and $148775.7, respectively. This is a much smaller difference. It means that as the size of houses increase, newness increases the price of the house more, per dollar.

Do you think the model with interaction or the one without it represents the relationship of size and new to the outcome price? What makes you prefer one model over another?

The model with interaction variables has a higher R-squared, and to me it makes sense that the cost of newness is seen in larger houses. Therefore I think the second model is the better one.