knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)
library(tidyverse)
library(ggplot2)
library(dplyr)
library(alr4)
library(smss)
library(stats)
library(stargazer)Error in library(stargazer): there is no package called 'stargazer'Emma Rasmussen
December 1, 2022
knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)
library(tidyverse)
library(ggplot2)
library(dplyr)
library(alr4)
library(smss)
library(stats)
library(stargazer)Error in library(stargazer): there is no package called 'stargazer' P S Be Ba New
1 48.5 1.10 3 1 0
2 55.0 1.01 3 2 0
3 68.0 1.45 3 2 0
4 137.0 2.40 3 3 0
5 309.4 3.30 4 3 1
6 17.5 0.40 1 1 0
Call:
lm(formula = P ~ S + Be + Ba + New, data = house.selling.price.2)
Residuals:
Min 1Q Median 3Q Max
-36.212 -9.546 1.277 9.406 71.953
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -41.795 12.104 -3.453 0.000855 ***
S 64.761 5.630 11.504 < 2e-16 ***
Be -2.766 3.960 -0.698 0.486763
Ba 19.203 5.650 3.399 0.001019 **
New 18.984 3.873 4.902 4.3e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 16.36 on 88 degrees of freedom
Multiple R-squared: 0.8689, Adjusted R-squared: 0.8629
F-statistic: 145.8 on 4 and 88 DF, p-value: < 2.2e-16##1a.
Beds would be deleted first in backwards elimintation because it has the highest p-value.
##1b.
For forward selection, size would be added first because it has the strongest correlation with price according the the correlation matrix.
##1c.
The BEDS variable is likely captured in the model by size and baths, so once all are included it is no longer significant.
##1d.
Using software with these four predictors, find the model that would be selected using each criterion:
Call:
lm(formula = P ~ S + Be + Ba + New, data = house.selling.price.2)
Residuals:
Min 1Q Median 3Q Max
-36.212 -9.546 1.277 9.406 71.953
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -41.795 12.104 -3.453 0.000855 ***
S 64.761 5.630 11.504 < 2e-16 ***
Be -2.766 3.960 -0.698 0.486763
Ba 19.203 5.650 3.399 0.001019 **
New 18.984 3.873 4.902 4.3e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 16.36 on 88 degrees of freedom
Multiple R-squared: 0.8689, Adjusted R-squared: 0.8629
F-statistic: 145.8 on 4 and 88 DF, p-value: < 2.2e-16fit_a<-lm(P~ S + Be + Ba + New, data=house.selling.price.2)
#All variables, and interaction term
summary(lm(P~ S + Be + Ba + New + S*New, data=house.selling.price.2))
Call:
lm(formula = P ~ S + Be + Ba + New + S * New, data = house.selling.price.2)
Residuals:
Min 1Q Median 3Q Max
-34.258 -8.823 0.561 11.581 39.564
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -30.214 11.461 -2.636 0.009926 **
S 58.874 5.361 10.982 < 2e-16 ***
Be -3.884 3.647 -1.065 0.289895
Ba 19.840 5.192 3.821 0.000249 ***
New -35.838 13.650 -2.625 0.010223 *
S:New 31.449 7.560 4.160 7.45e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.03 on 87 degrees of freedom
Multiple R-squared: 0.8906, Adjusted R-squared: 0.8843
F-statistic: 141.7 on 5 and 87 DF, p-value: < 2.2e-16fit_b<-lm(P~ S + Be + Ba + New + S*New, data=house.selling.price.2)
#Beds removed, with interatction
summary(lm(P~ S + Ba + New + S*New, data=house.selling.price.2))
Call:
lm(formula = P ~ S + Ba + New + S * New, data = house.selling.price.2)
Residuals:
Min 1Q Median 3Q Max
-35.319 -8.329 0.140 11.705 42.302
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -39.088 7.874 -4.964 3.35e-06 ***
S 55.496 4.325 12.831 < 2e-16 ***
Ba 21.041 5.072 4.149 7.69e-05 ***
New -35.661 13.660 -2.611 0.0106 *
S:New 30.855 7.545 4.089 9.54e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.04 on 88 degrees of freedom
Multiple R-squared: 0.8892, Adjusted R-squared: 0.8842
F-statistic: 176.5 on 4 and 88 DF, p-value: < 2.2e-16fit_c<-lm(P~ S + Ba + New + S*New, data=house.selling.price.2)
#Beds removed, no interaction
summary(lm(P~ S + Ba + New, data=house.selling.price.2))
Call:
lm(formula = P ~ S + Ba + New, data = house.selling.price.2)
Residuals:
Min 1Q Median 3Q Max
-34.804 -9.496 0.917 7.931 73.338
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -47.992 8.209 -5.847 8.15e-08 ***
S 62.263 4.335 14.363 < 2e-16 ***
Ba 20.072 5.495 3.653 0.000438 ***
New 18.371 3.761 4.885 4.54e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 16.31 on 89 degrees of freedom
Multiple R-squared: 0.8681, Adjusted R-squared: 0.8637
F-statistic: 195.3 on 3 and 89 DF, p-value: < 2.2e-16Error in stargazer(fit_a, fit_b, fit_c, fit_d, type = "text", style = "apsr"): could not find function "stargazer"###R2
The model with the highest R-squared is fit_b (all variables, and the interaction term between size and new)
lm(P~ S + Be + Ba + New + S*New)
###Adjusted R2
The model with the highest adjusted R-squared is also fit_b (but not by much, essentially the same R-squared as the same model without the BEDS variable, so I am skeptical this variable is useful)
lm(P~ S + Be + Ba + New + S*New)
###PRESS
Error in PRESS(fit_a): could not find function "PRESS"Error in PRESS(fit_b): could not find function "PRESS"Error in PRESS(fit_c): could not find function "PRESS"Error in PRESS(fit_d): could not find function "PRESS"The model with the lowest PRESS statistic is fit_c (with the interaction term but no BEDS variable) lm(P~ S + Ba + New + S*New)
###AIC
Because all models have 93 observations, we can compare AIC and BIC. The model that minimizes AIC is fit_c but fit_b is not much worse.
lm(P~ S + Ba + New + S*New)
###BIC
The model that minimizes BIC is fit_c. lm(P~ S + Ba + New + S*New)
##1e.
I prefer fit_c lm(P~ S + Ba + New + S*New) because it performs the best in terms of PRESS, AIC, and BIC, and about the same as the best one for adjusted R-squared. Because we have multiple variables included in the model I prefer to use adjusted R-squared over R-squared.
##2a.
(Data file: trees from base R) From the documentation: “This data set provides measurements of the diameter, height and volume of timber in 31 felled black cherry trees. Note that the diameter (in inches) is erroneously labeled Girth in the data. It is measured at 4 ft 6 in above the ground.”
Tree volume estimation is a big deal, especially in the lumber industry. Use the trees data to build a basic model of tree volume prediction. In particular,
fit a multiple regression model with the Volume as the outcome and Girth and Height as the explanatory variables Run regression diagnostic plots on the model. Based on the plots, do you think any of the regression assumptions is violated?
Girth Height Volume
1 8.3 70 10.3
2 8.6 65 10.3
3 8.8 63 10.2
4 10.5 72 16.4
5 10.7 81 18.8
6 10.8 83 19.7
Call:
lm(formula = Volume ~ Height + Girth, data = trees)
Residuals:
Min 1Q Median 3Q Max
-6.4065 -2.6493 -0.2876 2.2003 8.4847
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -57.9877 8.6382 -6.713 2.75e-07 ***
Height 0.3393 0.1302 2.607 0.0145 *
Girth 4.7082 0.2643 17.816 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.882 on 28 degrees of freedom
Multiple R-squared: 0.948, Adjusted R-squared: 0.9442
F-statistic: 255 on 2 and 28 DF, p-value: < 2.2e-16##2b.
Constant variance (of residuals) appears to be violated from these plots (Residuals vs Fitted is funnel shaped and Scale Location is not linear)
##3a.
Gore Bush Buchanan
ALACHUA 47300 34062 262
BAKER 2392 5610 73
BAY 18850 38637 248
BRADFORD 3072 5413 65
BREVARD 97318 115185 570
BROWARD 386518 177279 789
Call:
lm(formula = Buchanan ~ Bush, data = florida)
Residuals:
Min 1Q Median 3Q Max
-907.50 -46.10 -29.19 12.26 2610.19
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.529e+01 5.448e+01 0.831 0.409
Bush 4.917e-03 7.644e-04 6.432 1.73e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 353.9 on 65 degrees of freedom
Multiple R-squared: 0.3889, Adjusted R-squared: 0.3795
F-statistic: 41.37 on 1 and 65 DF, p-value: 1.727e-08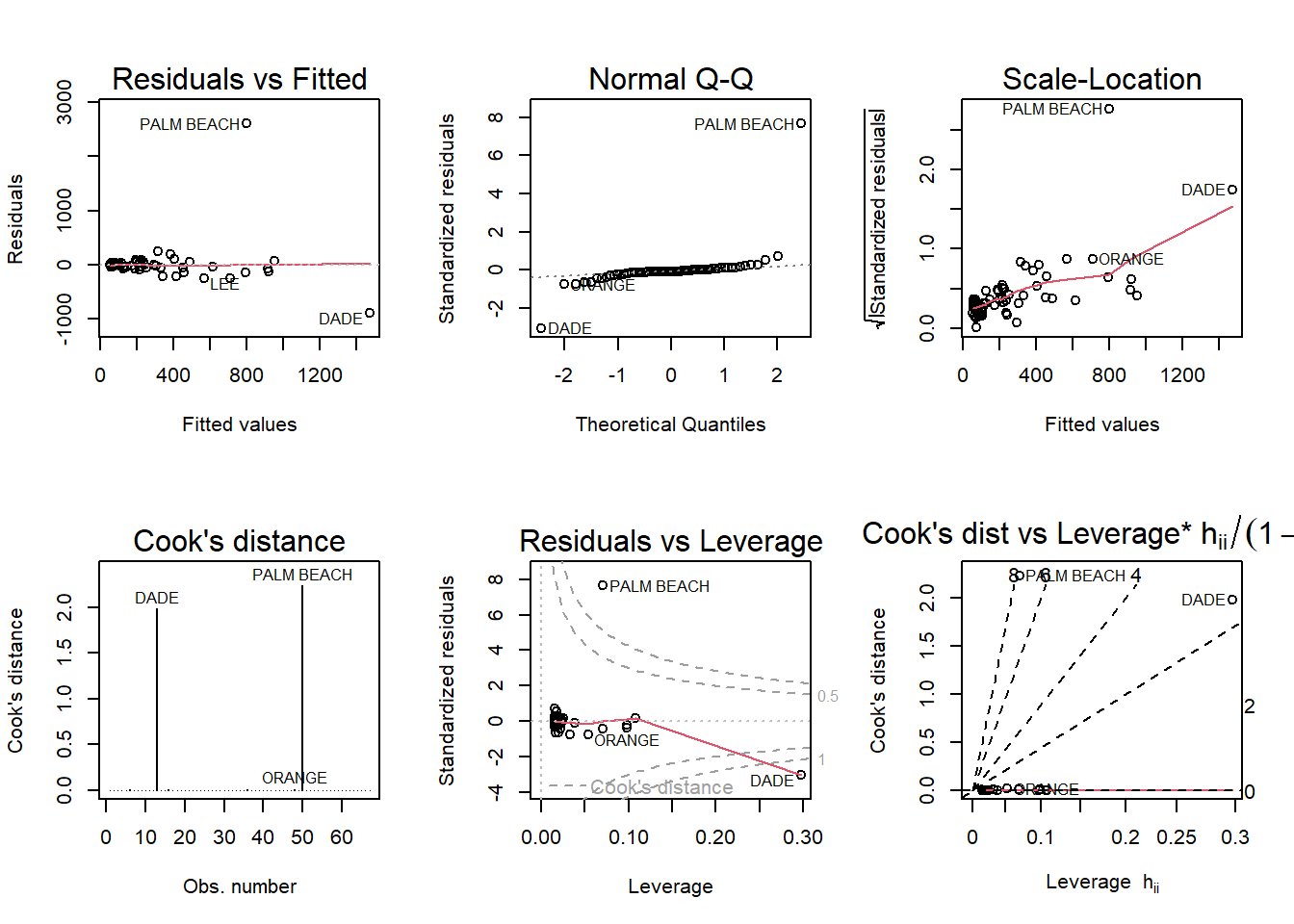
Palm Beach (and Dade) County appears to be an outlier. Cooks distance is greater than 1, and it has high leverage. ##3b.
Call:
lm(formula = log(Buchanan) ~ log(Bush), data = florida)
Residuals:
Min 1Q Median 3Q Max
-0.96075 -0.25949 0.01282 0.23826 1.66564
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.57712 0.38919 -6.622 8.04e-09 ***
log(Bush) 0.75772 0.03936 19.251 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4673 on 65 degrees of freedom
Multiple R-squared: 0.8508, Adjusted R-squared: 0.8485
F-statistic: 370.6 on 1 and 65 DF, p-value: < 2.2e-16fit_florida2<- (lm(log(Buchanan)~ log(Bush), data=florida))
par(mfrow= c(2,3)); plot(fit_florida2, which=1:6)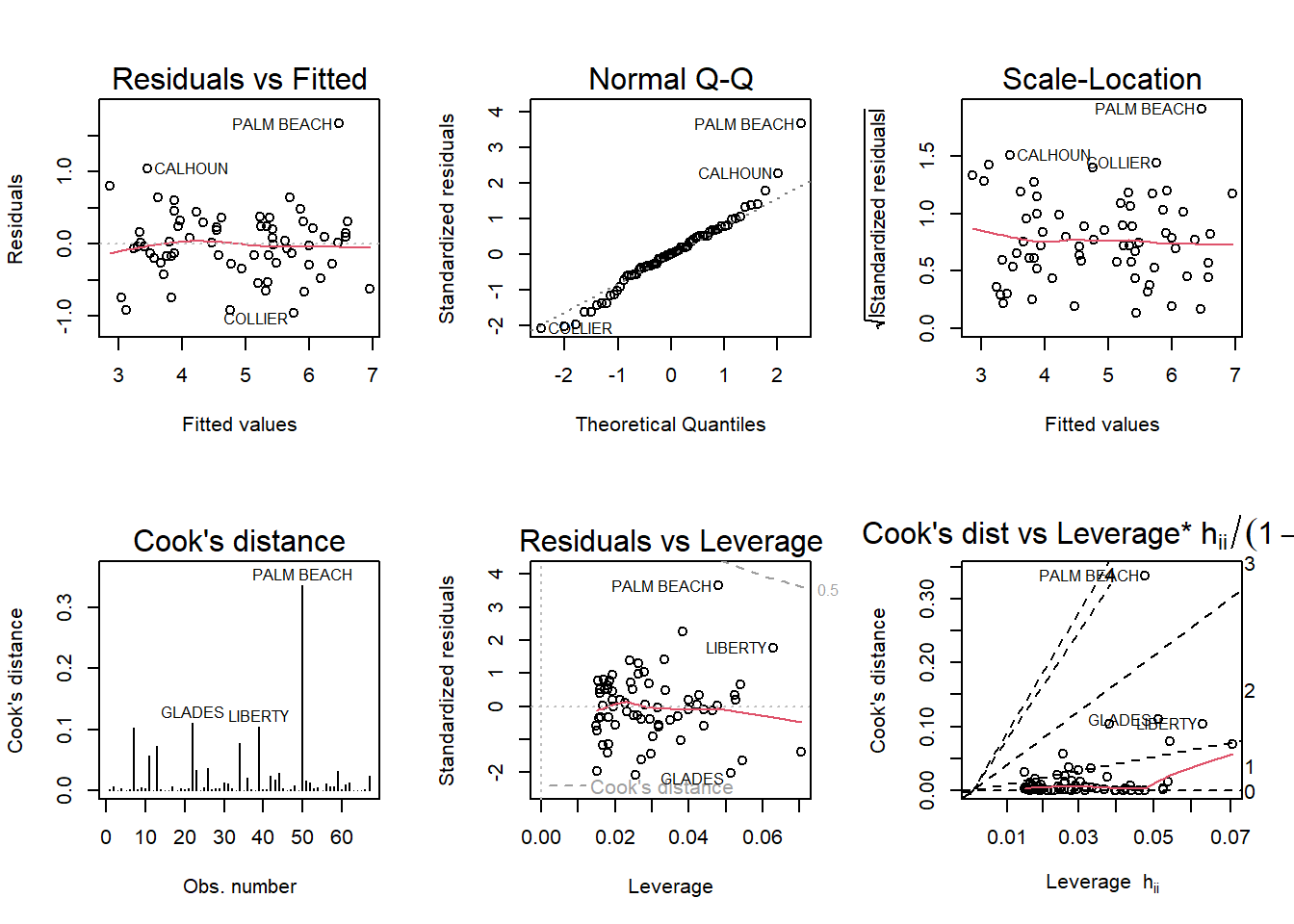
Palm beach could still be an potential outlier according to these plots, but the magnitude is less strong than in the previous plots.
---
title: "Homework 5"
date: "12/1/2022"
author: Emma Rasmussen
format:
html:
toc: true
code-copy: true
code-tools: true
categories:
- hw5
---
```{r}
#| label: setup
#| warning: false
#| message: false
knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)
library(tidyverse)
library(ggplot2)
library(dplyr)
library(alr4)
library(smss)
library(stats)
library(stargazer)
```
```{r}
data(house.selling.price.2)
head(house.selling.price.2)
summary(lm(P~ S + Be + Ba + New, data=house.selling.price.2))
```
##1a.
Beds would be deleted first in backwards elimintation because it has the highest p-value.
##1b.
For forward selection, size would be added first because it has the strongest correlation with price according the the correlation matrix.
##1c.
The BEDS variable is likely captured in the model by size and baths, so once all are included it is no longer significant.
##1d.
Using software with these four predictors, find the model that would be selected using each criterion:
```{r}
#All variables
summary(lm(P~ S + Be + Ba + New, data=house.selling.price.2))
fit_a<-lm(P~ S + Be + Ba + New, data=house.selling.price.2)
#All variables, and interaction term
summary(lm(P~ S + Be + Ba + New + S*New, data=house.selling.price.2))
fit_b<-lm(P~ S + Be + Ba + New + S*New, data=house.selling.price.2)
#Beds removed, with interatction
summary(lm(P~ S + Ba + New + S*New, data=house.selling.price.2))
fit_c<-lm(P~ S + Ba + New + S*New, data=house.selling.price.2)
#Beds removed, no interaction
summary(lm(P~ S + Ba + New, data=house.selling.price.2))
fit_d<-lm(P~ S + Ba + New, data=house.selling.price.2)
```
```{r}
stargazer(fit_a, fit_b, fit_c, fit_d, type= "text", style="apsr")
```
###R2
The model with the highest R-squared is fit_b (all variables, and the interaction term between size and new)
lm(P~ S + Be + Ba + New + S*New)
###Adjusted R2
The model with the highest adjusted R-squared is also fit_b (but not by much, essentially the same R-squared as the same model without the BEDS variable, so I am skeptical this variable is useful)
lm(P~ S + Be + Ba + New + S*New)
###PRESS
```{r}
PRESS(fit_a)
PRESS(fit_b)
PRESS(fit_c)
PRESS(fit_d)
```
The model with the lowest PRESS statistic is fit_c (with the interaction term but no BEDS variable)
lm(P~ S + Ba + New + S*New)
###AIC
Because all models have 93 observations, we can compare AIC and BIC. The model that minimizes AIC is fit_c but fit_b is not much worse.
lm(P~ S + Ba + New + S*New)
```{r}
AIC(fit_a)
AIC(fit_b)
AIC(fit_c)
AIC(fit_d)
```
###BIC
```{r}
BIC(fit_a)
BIC(fit_b)
BIC(fit_c)
BIC(fit_d)
```
The model that minimizes BIC is fit_c.
lm(P~ S + Ba + New + S*New)
##1e.
I prefer fit_c lm(P~ S + Ba + New + S*New) because it performs the best in terms of PRESS, AIC, and BIC, and about the same as the best one for adjusted R-squared. Because we have multiple variables included in the model I prefer to use adjusted R-squared over R-squared.
##2a.
(Data file: trees from base R)
From the documentation:
“This data set provides measurements of the diameter, height and volume of timber in 31 felled black cherry trees. Note that the diameter (in inches) is erroneously labeled Girth in the data. It is measured at 4 ft 6 in above the ground.”
Tree volume estimation is a big deal, especially in the lumber industry. Use the trees data to build a basic model of tree volume prediction. In particular,
fit a multiple regression model with the Volume as the outcome and Girth and Height as the explanatory variables
Run regression diagnostic plots on the model. Based on the plots, do you think any of the regression assumptions is violated?
```{r}
data(trees)
head(trees)
summary(lm(Volume ~ Height + Girth, data=trees))
fit_trees<-lm(Volume ~ Height + Girth, data=trees)
```
##2b.
```{r}
par(mfrow= c(2,3)); plot(fit_trees, which=1:6)
```
Constant variance (of residuals) appears to be violated from these plots (Residuals vs Fitted is funnel shaped and Scale Location is not linear)
##3a.
```{r}
data(florida)
head(florida)
```
```{r}
summary(lm(Buchanan~ Bush, data=florida))
fit_florida<- (lm(Buchanan~ Bush, data=florida))
par(mfrow= c(2,3)); plot(fit_florida, which=1:6)
```
Palm Beach (and Dade) County appears to be an outlier. Cooks distance is greater than 1, and it has high leverage.
##3b.
```{r}
summary(lm(log(Buchanan)~ log(Bush), data=florida))
fit_florida2<- (lm(log(Buchanan)~ log(Bush), data=florida))
par(mfrow= c(2,3)); plot(fit_florida2, which=1:6)
```
Palm beach could still be an potential outlier according to these plots, but the magnitude is less strong than in the previous plots.