Homework 5

Code

library(tidyverse)
library(smss)
library(alr4)
library(stargazer)

Error in library(stargazer): there is no package called 'stargazer'

Code

knitr::opts_chunk$set(echo = TRUE)

1a

I would delete Beds because it is the least significant variable to the regression equation. That would get deleted first because under backwards elimination, the variable least significant(the smallest P value) to the regression equation gets deleted first, and so on.

Code

#summary(lm(P ~ ., data = house.selling.price.2))

1b

Size would be added first because it has the highest t value at 11.5. Forward selection starts with no variables, then adds each one by how large their significance, or how large their t value is to the regression model.

1c

Correlation does not always equal causation. Beds does not have to be a significant variable for it to be correlated with Price. Also, when a sample size is small, it can account for the high p values in the regression model.

1d

Code

m1 <- lm(P ~., data = house.selling.price.2)

Error in is.data.frame(data): object 'house.selling.price.2' not found

Code

AIC(m1)

Error in AIC(m1): object 'm1' not found

Code

BIC(m1)

Error in BIC(m1): object 'm1' not found

Code

PRESS <- function(m1) {
  pr <- residuals(m1)/(1-lm.influence(m1)$hat)
  
  PRESS <- sum(pr^2)
  
  return(PRESS)
}

PRESS(m1)

Error in residuals(m1): object 'm1' not found

I needed assistance figuring out the PRESS statistic so I searched for functions to build online.

1e

With PRESS, you want a smaller number, which indicates better prediction of the model. Since the number appears to be ~28,000 (if I did the calculations correctly) I do not want to use PRESS. Instead, I would prefer the AIC model since it is the lowest score, indicating the best fit.

2a

Code

data(trees)

model <- lm(Volume ~ Girth + Height, data = trees)

#summary(model)

2b

Code

par(mfrow = c(2,3)); plot(model, which = 1:6)

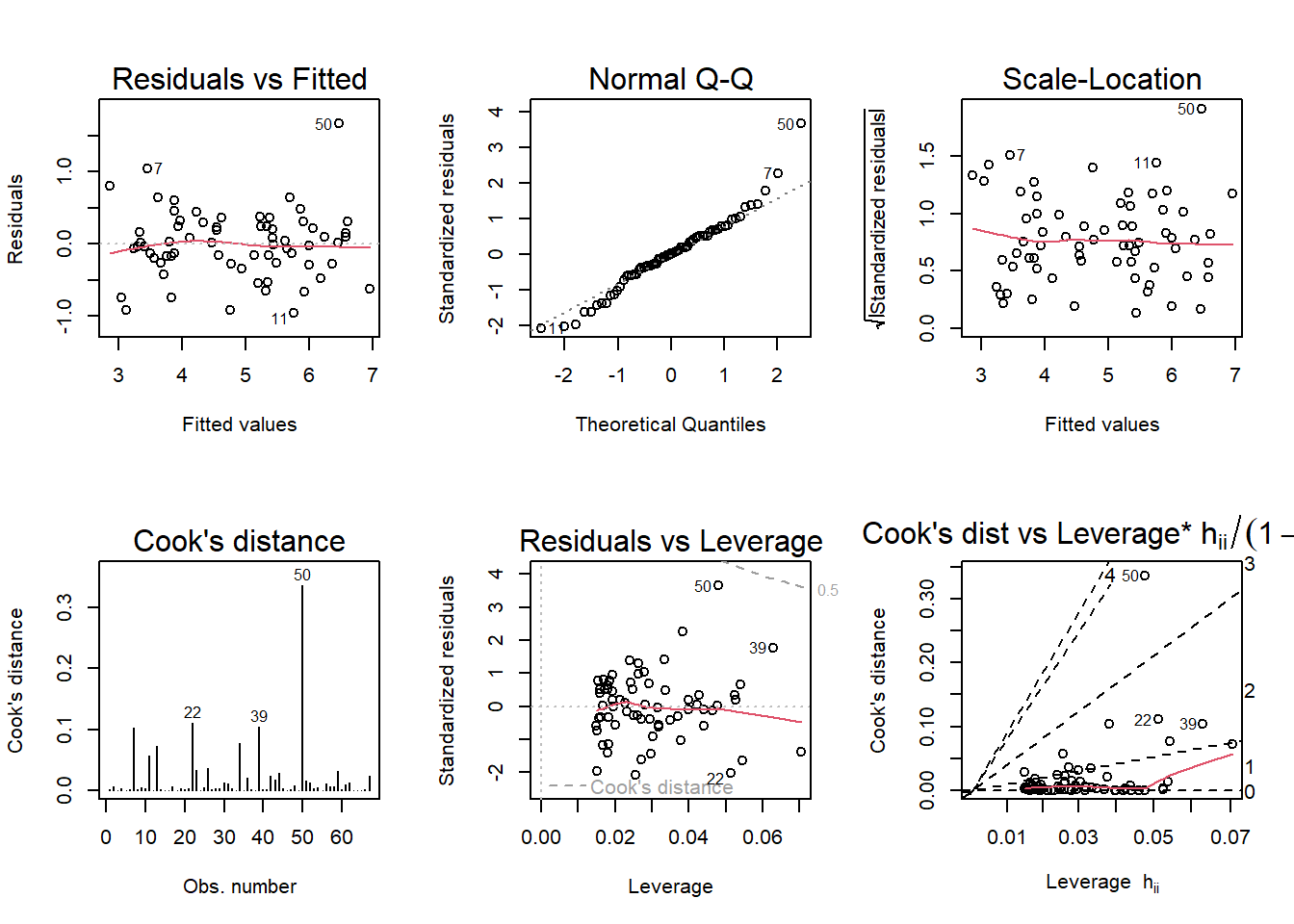
Linearity is violated because the residuals plot exhibits a curved line, not a horizontal line across zero. Assumption of equal variance is also violated because the plots are not too scattered. The line should be horizontal, but in this diagnostic plot, it is quite jagged. The QQ plot looks pretty linear so that one is fine the way it is suggesting the data follows a normal distribution. There are also no extreme values in the residuals vs leverage plot so there is nothing problematic there.

3a

Code

data("florida")


fit <- lm(Buchanan ~ Bush, data = florida)

I ran the linear regression and assigned it to the fit variable.

Code

par(mfrow = c(2,3))
plot(fit, which = 1:6)

It’s clear there is an outlier in each of the diagnostic plots. In each of the diagnostic plots, Palm Beach is a definite outlier among the other data points. Palm Beach County has almost 3,500 votes, the next highest in another county being 750. The residuals plot is normal with a horizontal line, but the residuals are not spread out which leads me to believe there is some violation. Palm Beach and Dade county both lay outside of Cook’s distance, meaning they are highly influential to the regression results.

3b

Code

fit2 <- lm(log(florida$Buchanan) ~ log(florida$Bush))


par(mfrow = c(2,3)); plot(fit2, which = 1:6)

From logging the variables, the QQ plot becomes linear and normalizes both residuals and scale-location plots. Residuals should “bounce around” the line at zero, which they do not do previously to logging the variables. When the variables are logged, it corrects this, making the data linear and demonstrates the relationship between the explanatory and outcome variables are linear.The normal QQ is also corrected showing the residuals are normally distributed with very little deviation. The scale location is how we check for homoskedasticity. When the variables are logged, the graph is perfect with a horizontal line and plots scattered a bit. It is the opposite of what we see in the graph when the variables are not logged. The residuals vs leverage extreme values are now inside of Cook’s distance so they will not impact the regression results. Logging the variables normalized all the results and seemed to resolve issues with the spread of the data. We should still note Palm Beach as the outlier.