Code
library(tidyverse)
library(dplyr)
library(ggplot2)
performance<- read_csv("_data/CompleteDataAndBiases.csv")
knitr::opts_chunk$set(echo = TRUE)Kalimah Muhammad
December 2, 2022
Researchers have examined the differences impacting student achievement among genders for decades. Early meta-analyses conducted by Hyde (1990) revealed no significant difference between the groups’ cognitive abilities; yet intelligence and self-perception of ability, or self-esteem, were determined as the strongest predictors of academic success (Spinath et al., 2010, Booth and Gerard, 2011). Some research explains differences in achievement partially by stereotype threat (ST). Stereotype threat, originally used to research the vulnerability of racial stereotypes on aptitude tests, is defined as “being at risk of confirming, as self-characteristic, a negative stereotype about one’s group” (Steele and Aronson, 1995). Conventional research has focused on gender differences to stereotype threat (Moè & Putwain, 2020), and two prevailing theories have emerged.
The first theory suggests that ST affects male and female students differently. Here male students achieve better outcomes when stereotype threat is present than stereotype lift, and the reverse is true for female students who are adversely impacted by stereotype threat and positively impacted by stereotype lift (Johnson et al., 2012). Other studies debunk this theory suggesting no evidence of ST as a phenomenon in female students (Warne, 2022), particularly in the domain of mathematical achievement (Ganley et al., 2013). A second theory exists that the effects of ST may not be fully realized as outcomes immediately but affect achievement over time as chronic ST impacts working memory and intellectual helplessness in girls’ math scores (Bedyńska, Krejtz, and Sedek, 2019) and male language arts scores (Bedyńska, Krejtz, and Sedek, 2020).
This study tests both theories. First, it questions if there are differences in predicted student achievement based on gender when exposed to negative stereotypes about males and positive stereotypes about females. Second, it evaluates the effect of the perceived prevalence of stereotypes as shown by the participants’ exposure to three types of stereotype activation in predicting grades. The types of stereotype activation include:
None: Participants were not exposed to stereotypes during this experiment.
Case-based: Participants were shown three student profiles in which one female student had a high grade, and two male students had low grades.
Statistics: Participants were shown statistics suggesting boys performed less well in school than girls.
This study tests the following hypotheses:
H1. Does exposure to negative stereotypes about male achievement (ST) and positive stereotypes of female achievement (SL) result in higher predicted achievement among both male and female students?
H2. Was there a statistically significant difference between predicted male and female achievement based on the type of stereotype activation?
Data for this project was collected from Kaggle (Performance vs. Predicted Performance, 2022) and is a collection of existing student performance data from a study by Cortez and Silva (2008) on predicting secondary school student performance and the collector’s addition of stereotype activation for machine learning. The data included information on actual student demographics such as gender, parents’ highest level of education, as well as time studying vs. free time, number of absences, and grade on a final exam, among other variables.
A few important variables to define include:
-Index - number of students included in the original and predicted data (N=856 of the original 991 students)
-Participant ID - number associated with participants making predictions (N=107)
-Sex - student’s sex (binary: ‘F’ - female or ‘M’ - male)
-Studytime - weekly study time is categorized as 1= less than 2 hours, 2= 2-5 hours and 3= 5+ hours
-Freetime - free time after school group as 1 = low, 2= medium, 3 = high
-Goout - how often a student goes out with friends where 1 is very low and 4 is very often
-Absences - number of school absences 1 - 7 where 7 represents any absences equal to or above 7
-Walc - weekend alcohol consumption
-Parents_edu - the higher of original variables mother’s edu and father’s edu, where 4 = the highest level of education
-G3 - final grade (numeric: from 0 to 20)
-Reason - The reason for why a student chose to go to the school in question. The levels are close to home, school’s reputation, school’s curricular and other
-PredictedGrade - the grade participants predicted based on actual data and their exposed level of StereotypeActivation
-StereotypeActivation - see three levels of stereotype activation above
-Pass - A binary variable showing whether G3 is a passing grade (i.e. >=10) or not
-PassFailStrategy - A binary variable showing whether the PredictedGrade is a passing grade (i.e. >=10) or not
An additional variable I added to the data set, STPresent, identifies whether stereotype activation was present (True or False) for participants when predicting student scores.
Below is a summary of the variables.
# A tibble: 10 × 19
index Parti…¹ name sex study…² freet…³ roman…⁴ Walc goout Paren…⁵ absen…⁶
<dbl> <dbl> <chr> <chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 132 1 Anna F 1 2 no 1 2 4 0
2 724 1 Mich… M 1 1 no 4 4 4 1
3 637 1 David M 1 2 no 4 2 2 0
4 884 1 Brian M 1 1 no 4 4 3 7
5 194 1 Jenny F 2 2 no 1 4 2 0
6 388 1 Oliv… M 2 2 no 1 1 4 1
7 65 1 Lisa F 2 3 no 2 3 4 1
8 303 1 Sarah F 3 3 yes 1 3 4 6
9 312 2 Oliv… M 3 2 yes 2 2 4 7
10 305 2 Lisa F 3 3 no 2 3 3 7
# … with 8 more variables: reason <chr>, G3 <dbl>, Pass <lgl>,
# PredictedGrade <dbl>, PredictedRank <dbl>, StereotypeActivation <chr>,
# Predicted_Pass_PassFailStrategy <lgl>,
# Predicted_Pass_RankingStrategy <lgl>, and abbreviated variable names
# ¹ParticipantID, ²studytime, ³freetime, ⁴romantic, ⁵Parents_edu, ⁶absences index ParticipantID name sex
Min. : 1.0 Min. : 1 Length:856 Length:856
1st Qu.:241.8 1st Qu.: 27 Class :character Class :character
Median :487.0 Median : 54 Mode :character Mode :character
Mean :486.9 Mean : 54
3rd Qu.:727.2 3rd Qu.: 81
Max. :990.0 Max. :107
studytime freetime romantic Walc
Min. :1.000 Min. :1.000 Length:856 Min. :1.000
1st Qu.:1.000 1st Qu.:2.000 Class :character 1st Qu.:1.000
Median :2.000 Median :2.000 Mode :character Median :2.000
Mean :1.887 Mean :2.183 Mean :2.284
3rd Qu.:2.000 3rd Qu.:3.000 3rd Qu.:3.000
Max. :3.000 Max. :3.000 Max. :4.000
goout Parents_edu absences reason
Min. :1.000 Min. :1.000 Min. :0.000 Length:856
1st Qu.:2.000 1st Qu.:2.000 1st Qu.:0.000 Class :character
Median :3.000 Median :3.000 Median :2.000 Mode :character
Mean :3.022 Mean :2.854 Mean :2.794
3rd Qu.:4.000 3rd Qu.:4.000 3rd Qu.:5.000
Max. :4.000 Max. :4.000 Max. :7.000
G3 Pass PredictedGrade PredictedRank
Min. : 1.00 Mode :logical Min. : 0.00 Min. :1.00
1st Qu.:10.00 FALSE:149 1st Qu.:10.00 1st Qu.:2.75
Median :12.00 TRUE :707 Median :14.00 Median :4.50
Mean :11.97 Mean :13.14 Mean :4.50
3rd Qu.:14.00 3rd Qu.:16.00 3rd Qu.:6.25
Max. :20.00 Max. :20.00 Max. :8.00
StereotypeActivation Predicted_Pass_PassFailStrategy
Length:856 Mode :logical
Class :character FALSE:170
Mode :character TRUE :686
Predicted_Pass_RankingStrategy STPresent
Mode :logical Mode :logical
FALSE:284 FALSE:264
TRUE :572 TRUE :592
STPresent
sex FALSE TRUE
F 132 296
M 132 296There is an even distribution of male and female students (428 each), with 69% of participants exposed to some type of stereotype activation during grade prediction. The actual and predicted rate of passing are similar, 707 students passed versus the predicted 686, approximately 83% to 80% respectively. This may suggest other variables as strong indicators in passing. There is, however, a notable difference in the average actual scores (11.97) and predicted scores (13.14). This is further emphasized by the median actual scores (12) and predicted median (14). This early finding suggest that although the rate of passing was slightly lower, the overall predicted scores are skewed higher than actual.
The next two graphs compare the actual final grade vs. the predicted grade for both genders.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.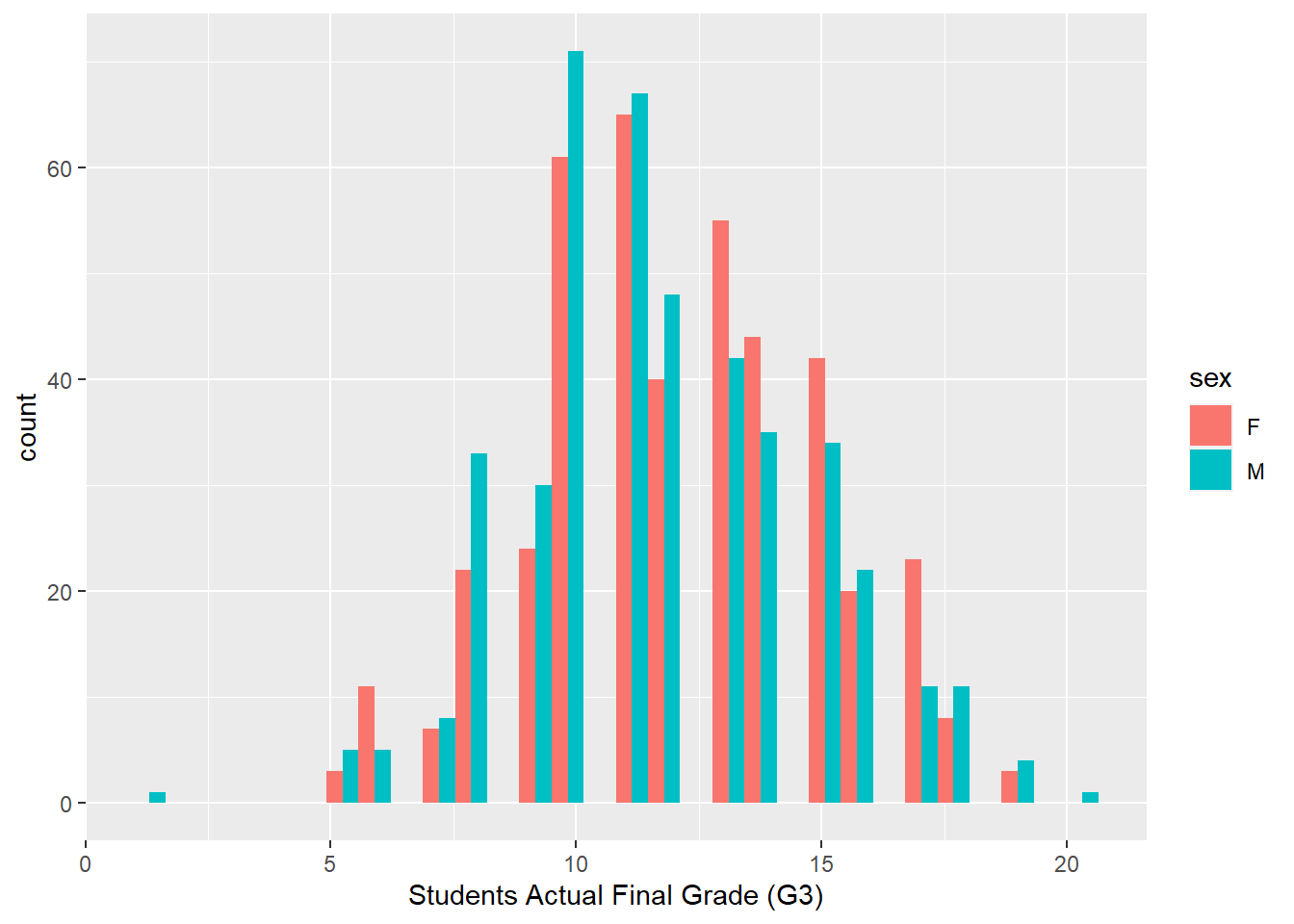
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.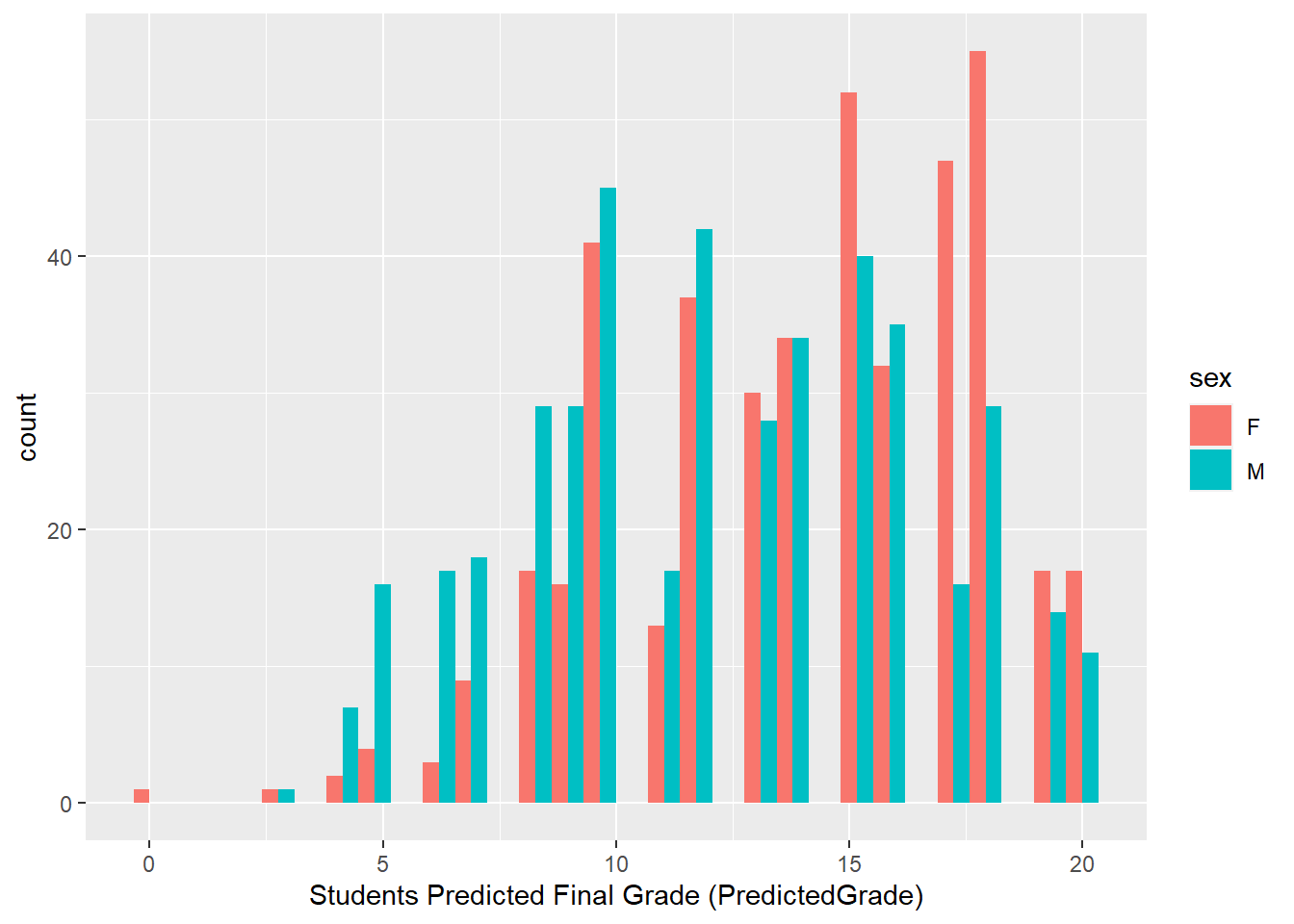
In the first graph, there is a fairly normal distribution of actual grades for both male and female students. Male students are more concentrated near the median value of 10 while female students are skewed slightly higher near the 11 value. However, in the second graph of predicted grades for both groups, female students are skewed significantly higher near 15 points while predictions for male students spreads near 12 points. This study will investigate if stereotype activation is a possible explanation for this variance.
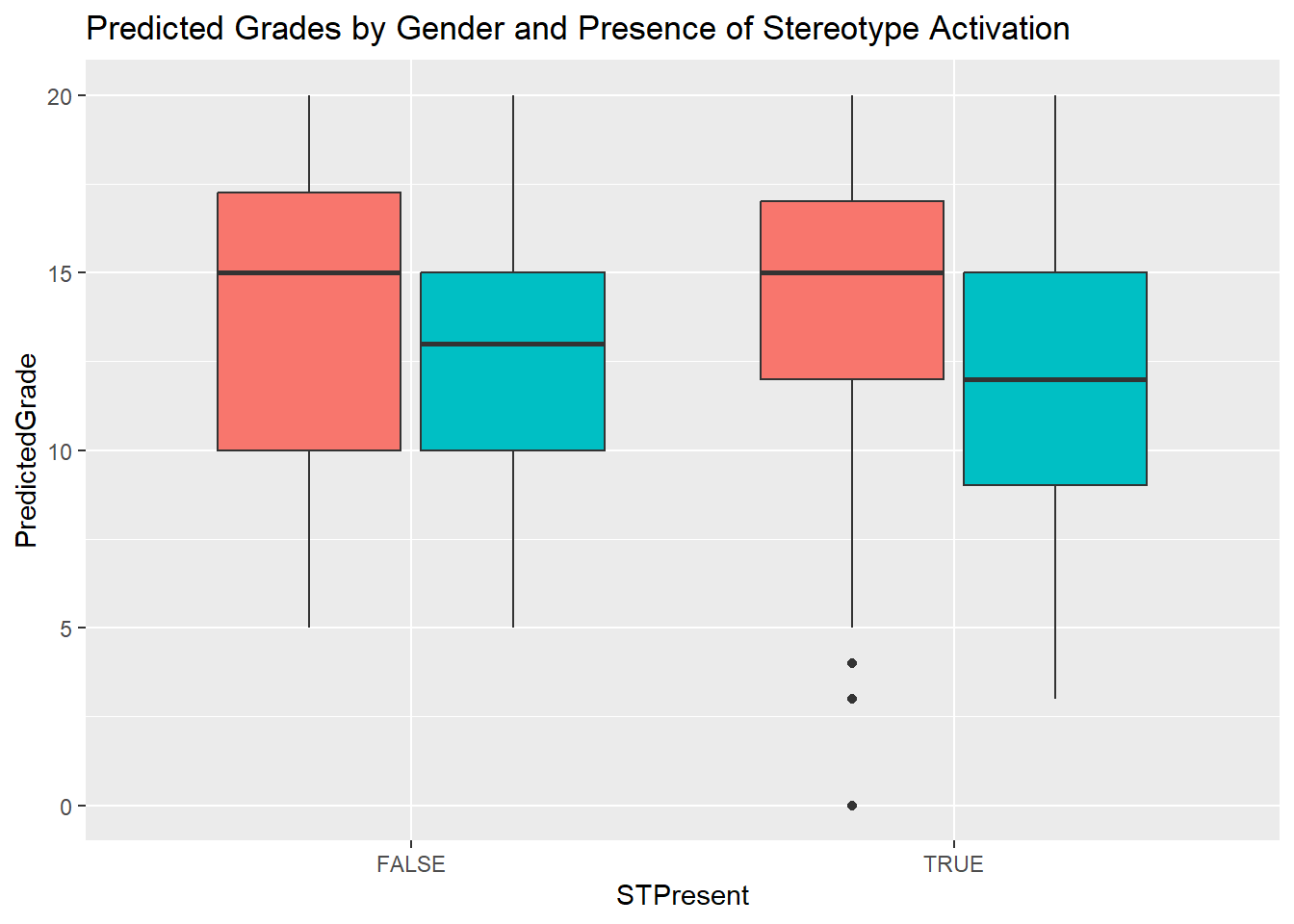
The chart above shows more variability in predicted grades for female students without any stereotype activation; yet once present, the concentration of scores skews higher. For male students, predicted scores increased in the presence of stereotype activation accounting for more low scores. Note, male scores were overall predicted lower than females independent of stereotype activation. Is there another variable contributing to this difference?
Here the dependent variable is the predicted grade and independent variable is presence of stereotype threat. The Null hypothesis states stereotype activation does not have a statistically significant effect on predicted grades for male and female students and the alternative hypothesis is negative stereotypes about male achievement and positive stereotypes of female achievement result in changes in predicted grades among both male and female students.
I conducted a two directional, two sample t-test to investigate the differences in the mean predicted score for students with it labeled “TRUE” and without stereotype activation labeled “FALSE”.
Welch Two Sample t-test
data: PredictedGrade by STPresent
t = 1.1314, df = 539.07, p-value = 0.2584
alternative hypothesis: true difference in means between group FALSE and group TRUE is not equal to 0
95 percent confidence interval:
-0.2409671 0.8955535
sample estimates:
mean in group FALSE mean in group TRUE
13.37121 13.04392 Although the mean predicted grades for those not exposed to ST are higher (13.37) compared to those where ST was present (13.04), the resulting p-value of 0.26, renders this test not significant in the predicted grades based on if stereotype activation was present. Thus, the null was retained.
The next test isolates predicted grades for male students only.
#create two tables for female students and male students
m_performance<-performance%>%
filter(sex=="M")
#t.test for difference in mean of predicted grades for males with and without ST present
#null hypothesis - mean of predicted grades is equals the mean of actual grades
t.test(PredictedGrade ~ STPresent, data= m_performance, alternative = c("two.sided"), conf.level = 0.95)
Welch Two Sample t-test
data: PredictedGrade by STPresent
t = 1.4747, df = 297.81, p-value = 0.1414
alternative hypothesis: true difference in means between group FALSE and group TRUE is not equal to 0
95 percent confidence interval:
-0.1975596 1.3787636
sample estimates:
mean in group FALSE mean in group TRUE
12.68182 12.09122 The following test isolates predicted grades for female students only.
#create two tables for female students and male students
m_performance<-performance%>%
filter(sex=="F")
#t.test for difference in mean of predicted grades for males with and without ST present
#null hypothesis - mean of predicted grades is equals the mean of actual grades
t.test(PredictedGrade ~ STPresent, data= f_performance, alternative = c("two.sided"), conf.level = 0.95)Error in eval(m$data, parent.frame()): object 'f_performance' not foundBoth tests have a p-value higher than 0.05 denoting that neither gender experienced a statistically significant difference in predicted average grades based on exposure to stereotype activation or not. Further rejecting hypothesis one.
The graph below calculates the mean predicted grade for both groups based on the type of stereotype activation.
`summarise()` has grouped output by 'sex'. You can override using the `.groups`
argument.# A tibble: 6 × 5
# Groups: sex [2]
sex StereotypeActivation `mean(PredictedGrade)` `mean(G3)` mean(PredictedG…¹
<chr> <chr> <dbl> <dbl> <dbl>
1 F CaseBased 13.4 12.2 1.22
2 F None 14.1 12.3 1.80
3 F Statistics 14.5 12.0 2.47
4 M CaseBased 12.0 11.6 0.353
5 M None 12.7 11.8 0.932
6 M Statistics 12.2 12.0 0.212
# … with abbreviated variable name ¹`mean(PredictedGrade) - mean(G3)`In the summary above, participants ranked the average predicted scores higher overall than the actual scores irrespective of gender or stereotype activation. The difference in predicted versus actual score was greatest among female students. Here participants exposed to the stereotype statistics predicted the widest difference compared to actual scores (2.47) and the highest overall scores (14.5).
For male students, predictions were closer to the average actual performance (11.80) ranging at a difference of 0.16 - 0.88 points. With no stereotype activation, males students garnered their highest predicted average at 12.68 suggesting introducing stereotypes negatively affected predictions in male students although still higher than actual performance. For female students, introducing statistics of lower male performance than females garnered the highest grade prediction for female students. For both genders, case based stereotype activation which included one example of a high female score and two examples of lower male scores produced the lowest predicted grades.
Pairwise comparisons using t tests with pooled SD
data: performance$PredictedGrade and performance$StereotypeActivation
CaseBased None
None 0.047 -
Statistics 0.044 0.949
P value adjustment method: none This may suggest that other variables in the study have an influential role in predicting scores outside of stereotype activation.
In the first model, I will use PredictedGrade as the outcome or dependent variable and the STPresent variable as the explanatory or independent variable adding in student sex as an interaction term.
Call:
lm(formula = PredictedGrade ~ STPresent * sex, data = performance)
Residuals:
Min 1Q Median 3Q Max
-13.9966 -3.0126 0.0034 3.0034 7.9088
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.06061 0.34139 41.186 <2e-16 ***
STPresentTRUE -0.06398 0.41052 -0.156 0.8762
sexM -1.37879 0.48280 -2.856 0.0044 **
STPresentTRUE:sexM -0.52662 0.58056 -0.907 0.3646
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.922 on 852 degrees of freedom
Multiple R-squared: 0.04948, Adjusted R-squared: 0.04613
F-statistic: 14.78 on 3 and 852 DF, p-value: 2.165e-09Here we find in the absence of stereotype activation, gender is a statistically significant predictor of grades as represented by p-values under 0.05 and higher p-values when ST is present. However, the overall model of presence of stereotype activation and gender are not significant in predicting grades with a p-value of 2.17. This model confirms earlier hypothesis testing results that mean predicted grades based on ST is not as significant but gender may play a role.
The next two models address the second hypothesis and distinguishes the stereotype activation by type, adding the sex variable as both a second explanatory variable (model 2) and an interaction term (model 3).
Call:
lm(formula = PredictedGrade ~ StereotypeActivation + sex, data = performance)
Residuals:
Min 1Q Median 3Q Max
-13.5553 -2.8123 0.4447 3.1877 8.1877
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.5553 0.2725 49.752 < 2e-16 ***
StereotypeActivationNone 0.6874 0.3382 2.033 0.0424 *
StereotypeActivationStatistics 0.6662 0.3228 2.064 0.0394 *
sexM -1.7430 0.2676 -6.514 1.25e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.914 on 852 degrees of freedom
Multiple R-squared: 0.0533, Adjusted R-squared: 0.04996
F-statistic: 15.99 on 3 and 852 DF, p-value: 4.046e-10
Call:
lm(formula = PredictedGrade ~ StereotypeActivation * sex, data = performance)
Residuals:
Min 1Q Median 3Q Max
-13.4044 -2.9632 0.4091 3.0368 8.0368
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.40441 0.33554 39.948 < 2e-16 ***
StereotypeActivationNone 0.65619 0.47811 1.372 0.17028
StereotypeActivationStatistics 1.09559 0.45639 2.401 0.01658 *
sexM -1.44118 0.47453 -3.037 0.00246 **
StereotypeActivationNone:sexM 0.06239 0.67615 0.092 0.92651
StereotypeActivationStatistics:sexM -0.85882 0.64543 -1.331 0.18367
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.913 on 850 degrees of freedom
Multiple R-squared: 0.05618, Adjusted R-squared: 0.05063
F-statistic: 10.12 on 5 and 850 DF, p-value: 1.989e-09Analysis of Variance Table
Model 1: PredictedGrade ~ StereotypeActivation + sex
Model 2: PredictedGrade ~ StereotypeActivation * sex
Res.Df RSS Df Sum of Sq F Pr(>F)
1 852 13055
2 850 13015 2 39.769 1.2986 0.2734In both models, there is a significance to introducing case based ST for both genders, negatively for male students and positively for female students. The use of statistics garnered less significance for both genders, however still significant for predicting mean grades for female students. Once again the highest predicted scores for males were under conditions when ST was not present.
Comparing the two models, results are similar and there is minimal increase in the R-squared (0.053 to 0.056) and adjusted R-squared (0.050 to 0.051) for using sex as an explanatory variable vs. an interaction term. Residuals are also lower in model 3 than for model 2. The analysis of variance for the two models also confirms this result with lower RSS for model 3, minimizing residuals in the model. Thus model 3 is a better fit than model two.
Until now, I investigated stereotype activation as the primary explanatory variable in predicting grades for both genders. However, in both my hypothesis testing and previous models, this variable was not significant in comparing scores with or without the presence of stereotype activation. This next model explores which of the other variables could explain this phenomena including gender as an interaction term.
Variables selected for exploration include:
-Studytime - weekly study time is categorized as 1= less than 2 hours, 2= 2-5 hours and 3= 5+ hours
-Freetime - free time after school group as 1 = low, 2= medium, 3 = high
-Goout - how often a student goes out with friends where 1 is very low and 4 is very often
-Absences - number of school absences 1 - 7 where 7 represents any absences equal to or above 7
-Walc - weekend alcohol consumption
-Parents_edu - the higher of original variables mother’s edu and father’s edu, where 4 = the highest level of education
# A tibble: 2 × 7
sex `mean(studytime)` `mean(freetime)` `mean(goout)` mean(…¹ mean(…² mean(…³
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 F 2.07 2.07 2.99 2.70 12.1 14.0
2 M 1.71 2.30 3.05 2.89 11.8 12.3
# … with abbreviated variable names ¹`mean(absences)`, ²`mean(G3)`,
# ³`mean(PredictedGrade)`The above tables summarize differences in the mean values for several variables of interest by gender. Here we see, female students score slightly higher in study time (2.07 vs. 1.7) and while lower in free time (2.07 vs, 2.3), goout (3 vs. 3.05), absences (2.7 vs. 2.9). These would suggest female students may have a higher predicted grade based on good practices which is proven by the actual grades in G3 (12.15 vs. 11.80). However, there is larger discrepancies in predicted rages (14.0 for females vs. 12.28 for males).
Call:
lm(formula = PredictedGrade ~ (studytime + freetime + Walc +
goout + Parents_edu + absences) * sex, data = performance)
Residuals:
Min 1Q Median 3Q Max
-14.1916 -2.2127 0.2298 2.2908 9.5489
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 12.20702 0.90896 13.430 < 2e-16 ***
studytime 1.70283 0.23838 7.143 1.97e-12 ***
freetime 0.32324 0.22396 1.443 0.149303
Walc -0.57563 0.16305 -3.530 0.000437 ***
goout -0.43723 0.18408 -2.375 0.017763 *
Parents_edu 0.40536 0.15127 2.680 0.007512 **
absences -0.38691 0.05807 -6.663 4.83e-11 ***
sexM -1.02714 1.30371 -0.788 0.431000
studytime:sexM -0.25917 0.33611 -0.771 0.440867
freetime:sexM -0.33562 0.30899 -1.086 0.277716
Walc:sexM -0.13419 0.22607 -0.594 0.552946
goout:sexM 0.36529 0.27901 1.309 0.190810
Parents_edu:sexM 0.29052 0.22058 1.317 0.188168
absences:sexM -0.07768 0.08359 -0.929 0.352963
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.279 on 842 degrees of freedom
Multiple R-squared: 0.3435, Adjusted R-squared: 0.3334
F-statistic: 33.9 on 13 and 842 DF, p-value: < 2.2e-16Analysis of Variance Table
Model 1: PredictedGrade ~ StereotypeActivation * sex
Model 2: PredictedGrade ~ (studytime + freetime + Walc + goout + Parents_edu +
absences) * sex
Res.Df RSS Df Sum of Sq F Pr(>F)
1 850 13015.3
2 842 9052.6 8 3962.7 46.073 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1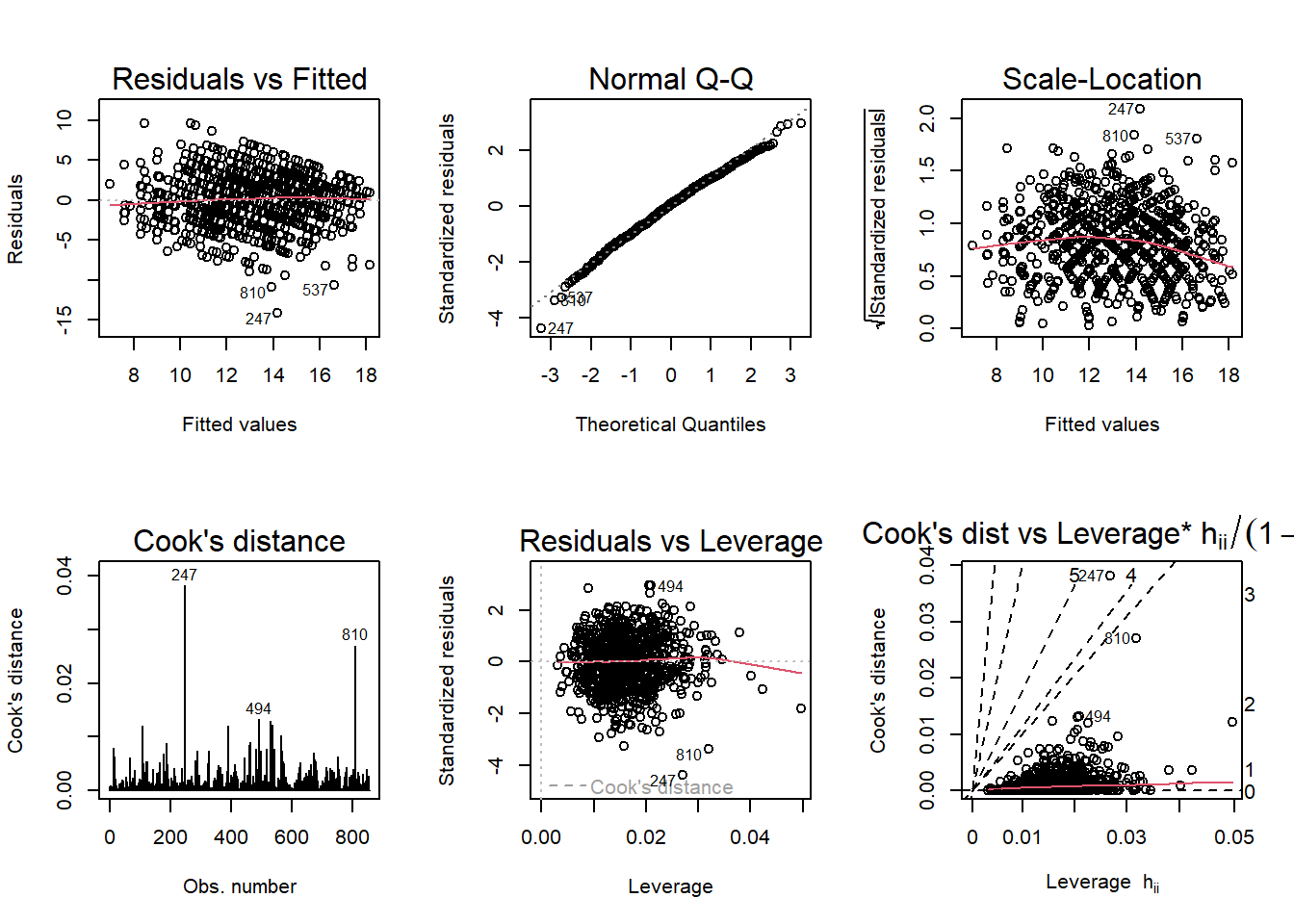
In this final model, we find similar residuals to model 3 but a large increase in the R-squared (0.057 to 0.34), adjusted r-squared values (0.051 to 0.33) and F-statistic (10.12 on 5 to 33.9 on 13). Based on the p-values, we also note study time, weekly alcohol consumption, parents education, and number of absences as most significant in predicting mean grades. Female students scored slighly more favorably in each of these areas than male students accounting a slight increase in actual grades as well. Thus perhaps participants over-estimated these values in predicting grades.
Comparing model 4 to model 3 using analysis of variance, there is a significant reduction in RSS and increase in p-value significance suggesting the introduction of these behavioral variables as a better fit for predicting grades than the introduction of stereotype activation. Note that in diagnosis the model 4 there are issues in normality (see the Cook’s distance and Residuals vs. Leverage plots) as well as heteroskedasticity (see the Scale-Location plot). Since further evaluation of these variables are outside of the scope of this project, I will select model 3 for diagnostics.
For this section, I will evaluate a few assumptions with model 3 which aimed to predict grades by the type of stereotype activation and the sex variable as an interaction term.
Normality of Errors - In the Normal Q-Q plot, most observations fall close to the line assuming normality. Using the Cook’s Distance and Residuals vs. Leverage, we can assume residuals are mostly normal as well with the exception of observation #62 whose leverage makes it an influential observation.
Linearity - Viewing the Residuals vs. Fitted plot, we see a relatively straight and horizontal line suggesting the average residual for the fitted values are relatively similar. Note, there are three observations, #62, #348, and #742 that are identified as outliers.
Equal Variance of Errors - Although the Residuals vs. Fitted plot show a near equal variance of the error terms based on its straight and horizontal line, the Scale-Location plot shows a decreasing rather than flat trend as the fitted values increase.
In summary, stereotype activation has some influence in predicting higher scores for certain groups under certain conditions but was not a statistically significant predictor in grades for either male or female students based on this experiment. In this study, stereotypes favored female students over male students. Where this stereotype was present for both case based and statistic stereotypes, there was an increase in female predicted scores versus when ST was absent. Predictions for male grades also benefited from a higher predicted score when ST was absent. This does suggest there is some bias introduced with stereotype activation but not enough to be statistically significant in predicting grades.
A more robust model for predicting grades (model 4) incorporated student behavioral factors such as study time, weekly alcohol consumption, and number of school absences as well demographic factors such as parents education. Future research should further investigate these variables as well as test the inverse of the stereotype which would favor male students. Overall, participants generally predicted grades higher for both genders compared to actual but the average predicted scores were not statistically significant based on stereotype activation.
Bedyńska, S., Krejtz, I. & Sedek, G. Chronic stereotype threat and mathematical achievement in age cohorts of secondary school girls: mediational role of working memory, and intellectual helplessness. Soc Psychol Educ 22, 321–335 (2019). https://doi.org/10.1007/s11218-019-09478-6
Bedyńska, S., Krejtz, I., Rycielski, P. et al. Stereotype threat as an antecedent to domain identification and achievement in language arts in boys: a cross-sectional study. Soc Psychol Educ 23, 755–771 (2020). https://doi.org/10.1007/s11218-020-09557-z
Booth MZ, Gerard JM. Self-esteem and academic achievement: a comparative study of adolescent students in England and the United States. Compare. 2011 Sep;41(5):629-648. doi: 10.1080/03057925.2011.566688
Cortez, P. and Silva, A. Using Data Mining to Predict Secondary School Student Performance. In A. Brito and J. Teixeira Eds., Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) pp. 5-12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978-9077381-39-7
Ganley, C. M., Mingle, L. A., Ryan, A. M., Ryan, K., Vasilyeva, M., & Perry, M. (2013). An examination of stereotype threat effects on girls’ mathematics performance. Developmental Psychology, 49(10), 1886–1897. https://doi.org/10.1037/a0031412
Hyde, Janet Shibley. “Meta-analysis and the psychology of gender differences.” Signs: Journal of Women in Culture and Society 16.1 (1990): 55-73.
Johnson, H., Barnard-Brak, L., Saxon, T., & Johnson, M.K. (2012) An Experimental Study of the Effects of Stereotype Threat and Stereotype Lift on Men and Women’s Performance in Mathematics, The Journal of Experimental Education, 80:2, 137-149, DOI: 10.1080/00220973.2011.567312
Moè, A., & Putwain, D. W. (2020). An evaluative message fosters mathematics performance in male students but decreases intrinsic motivation in female students. Educational Psychology, 1–20. https://doi.org/10.1080/01443410.2020.1730767
Spinath, B., Harald Freudenthaler, H., & Neubauer, A. C. (2010). Domain-specific school achievement in boys and girls as predicted by intelligence, personality and motivation. Personality and Individual Differences, 48(4), 481-486. https://doi.org/10.1016/j.paid.2009.11.028
Steele, Claude M., and Joshua Aronson. “Stereotype threat and the intellectual test performance of African Americans.” Journal of personality and social psychology 69.5 (1995): 797.
Warne, R. T. (2022). No Strong Evidence of Stereotype Threat in Females: A Reassessment of the Meta-Analysis. Journal of Advanced Academics, 33(2), 171–186. https://doi.org/10.1177/1932202X211061517
Data source: Anonymous. (2022). Performance vs. Predicted Performance[Data set]. Kaggle. https://doi.org/10.34740/KAGGLE/DSV/4282405
---
title: "Final Pt.2: Updates"
author: "Kalimah Muhammad"
desription: "Updates to Final Part 2"
date: "12/02/2022"
format:
html:
toc: true
code-fold: true
code-copy: true
code-tools: true
categories:
- finalpt2
- Kalimah Muhammad
---
```{r}
#| label: setup
#| warning: FALSE
library(tidyverse)
library(dplyr)
library(ggplot2)
performance<- read_csv("_data/CompleteDataAndBiases.csv")
knitr::opts_chunk$set(echo = TRUE)
```
## Background
Researchers have examined the differences impacting student achievement among genders for decades. Early meta-analyses conducted by Hyde (1990) revealed no significant difference between the groups' cognitive abilities; yet intelligence and self-perception of ability, or self-esteem, were determined as the strongest predictors of academic success (Spinath et al., 2010, Booth and Gerard, 2011). Some research explains differences in achievement partially by stereotype threat (ST). Stereotype threat, originally used to research the vulnerability of racial stereotypes on aptitude tests, is defined as "being at risk of confirming, as self-characteristic, a negative stereotype about one's group" (Steele and Aronson, 1995). Conventional research has focused on gender differences to stereotype threat (Moè & Putwain, 2020), and two prevailing theories have emerged.
The first theory suggests that ST affects male and female students differently. Here male students achieve better outcomes when stereotype threat is present than stereotype lift, and the reverse is true for female students who are adversely impacted by stereotype threat and positively impacted by stereotype lift (Johnson et al., 2012). Other studies debunk this theory suggesting no evidence of ST as a phenomenon in female students (Warne, 2022), particularly in the domain of mathematical achievement (Ganley et al., 2013). A second theory exists that the effects of ST may not be fully realized as outcomes immediately but affect achievement over time as chronic ST impacts working memory and intellectual helplessness in girls' math scores (Bedyńska, Krejtz, and Sedek, 2019) and male language arts scores (Bedyńska, Krejtz, and Sedek, 2020).
## Research Questions
This study tests both theories. First, it questions if there are differences in predicted student achievement based on gender when exposed to negative stereotypes about males and positive stereotypes about females. Second, it evaluates the effect of the perceived prevalence of stereotypes as shown by the participants' exposure to three types of stereotype activation in predicting grades. The types of stereotype activation include:
- None: Participants were not exposed to stereotypes during this experiment.
- Case-based: Participants were shown three student profiles in which one female student had a high grade, and two male students had low grades.
- Statistics: Participants were shown statistics suggesting boys performed less well in school than girls.
This study tests the following hypotheses:
**H1.** Does exposure to negative stereotypes about male achievement (ST) and positive stereotypes of female achievement (SL) result in higher predicted achievement among both male and female students?
**H2.** Was there a statistically significant difference between predicted male and female achievement based on the type of stereotype activation?
## Data
Data for this project was collected from Kaggle (Performance vs. Predicted Performance, 2022) and is a collection of existing student performance data from a study by Cortez and Silva (2008) on predicting secondary school student performance and the collector's addition of stereotype activation for machine learning. The data included information on actual student demographics such as gender, parents' highest level of education, as well as time studying vs. free time, number of absences, and grade on a final exam, among other variables.
A few important variables to define include:\
-Index - number of students included in the original and predicted data (N=856 of the original 991 students)\
-Participant ID - number associated with participants making predictions (N=107)\
-Sex - student's sex (binary: 'F' - female or 'M' - male)\
-Studytime - weekly study time is categorized as 1= less than 2 hours, 2= 2-5 hours and 3= 5+ hours\
-Freetime - free time after school group as 1 = low, 2= medium, 3 = high\
-Goout - how often a student goes out with friends where 1 is very low and 4 is very often\
-Absences - number of school absences 1 - 7 where 7 represents any absences equal to or above 7\
-Walc - weekend alcohol consumption\
-Parents_edu - the higher of original variables mother's edu and father's edu, where 4 = the highest level of education\
-G3 - final grade (numeric: from 0 to 20)\
-Reason - The reason for why a student chose to go to the school in question. The levels are close to home, school's reputation, school's curricular and other\
-PredictedGrade - the grade participants predicted based on actual data and their exposed level of StereotypeActivation\
-StereotypeActivation - see three levels of stereotype activation above\
-Pass - A binary variable showing whether G3 is a passing grade (i.e. \>=10) or not\
-PassFailStrategy - A binary variable showing whether the PredictedGrade is a passing grade (i.e. \>=10) or not
An additional variable I added to the data set, STPresent, identifies whether stereotype activation was present (True or False) for participants when predicting student scores.
Below is a summary of the variables.
```{r, summary of data}
#view top 5 observations
head(performance, 10)
#Add column that distinguishes if stereotype activation is present
performance <-performance%>%
mutate(STPresent = case_when(StereotypeActivation == "CaseBased"| StereotypeActivation == "Statistics" ~ TRUE, StereotypeActivation=="None" ~ FALSE))
summary(performance)
#cross-tabulation of stereotype activation by gender
xtabs(~sex + STPresent, performance)
```
There is an even distribution of male and female students (428 each), with 69% of participants exposed to some type of stereotype activation during grade prediction. The actual and predicted rate of passing are similar, 707 students passed versus the predicted 686, approximately 83% to 80% respectively. This may suggest other variables as strong indicators in passing. There is, however, a notable difference in the average actual scores (11.97) and predicted scores (13.14). This is further emphasized by the median actual scores (12) and predicted median (14). This early finding suggest that although the rate of passing was slightly lower, the overall predicted scores are skewed higher than actual.
The next two graphs compare the actual final grade vs. the predicted grade for both genders.
```{r, plot actual and predicted performance}
ggplot(performance, aes(x=G3, fill=sex))+ geom_histogram(position = "dodge")+labs(x="Students Actual Final Grade (G3)")
ggplot(performance, aes(x=PredictedGrade, fill=sex))+ geom_histogram(position = "dodge")+labs(x="Students Predicted Final Grade (PredictedGrade)")
```
In the first graph, there is a fairly normal distribution of actual grades for both male and female students. Male students are more concentrated near the median value of 10 while female students are skewed slightly higher near the 11 value. However, in the second graph of predicted grades for both groups, female students are skewed significantly higher near 15 points while predictions for male students spreads near 12 points. This study will investigate if stereotype activation is a possible explanation for this variance.
```{r, boxplot of grades by ST presence}
#boxplot of predicted grades by gender and if stereotype activation is present
ggplot(performance, aes(x=STPresent, y=PredictedGrade, fill=sex))+
geom_boxplot()+
theme(legend.position="none") +
ggtitle("Predicted Grades by Gender and Presence of Stereotype Activation")
```
The chart above shows more variability in predicted grades for female students without any stereotype activation; yet once present, the concentration of scores skews higher. For male students, predicted scores increased in the presence of stereotype activation accounting for more low scores. Note, male scores were overall predicted lower than females independent of stereotype activation. Is there another variable contributing to this difference?
## Hypothesis Testing
### *H1. Does exposure to negative stereotypes about male achievement (ST) and positive stereotypes of female achievement (SL) result in differences in predicted achievement among both male and female students?*
Here the dependent variable is the predicted grade and independent variable is presence of stereotype threat. The Null hypothesis states stereotype activation does not have a statistically significant effect on predicted grades for male and female students and the alternative hypothesis is negative stereotypes about male achievement and positive stereotypes of female achievement result in changes in predicted grades among both male and female students.
I conducted a two directional, two sample t-test to investigate the differences in the mean predicted score for students with it labeled "TRUE" and without stereotype activation labeled "FALSE".
```{r, t-test 1}
t.test(PredictedGrade ~ STPresent, data= performance, alternative = c("two.sided"), var.equal = FALSE, conf.level = 0.95)
```
Although the mean predicted grades for those not exposed to ST are higher (13.37) compared to those where ST was present (13.04), the resulting p-value of 0.26, renders this test not significant in the predicted grades based on if stereotype activation was present. Thus, the null was retained.
The next test isolates predicted grades for male students only.
```{r, t-test male}
#create two tables for female students and male students
m_performance<-performance%>%
filter(sex=="M")
#t.test for difference in mean of predicted grades for males with and without ST present
#null hypothesis - mean of predicted grades is equals the mean of actual grades
t.test(PredictedGrade ~ STPresent, data= m_performance, alternative = c("two.sided"), conf.level = 0.95)
```
The following test isolates predicted grades for female students only.
```{r, t-test female}
#create two tables for female students and male students
m_performance<-performance%>%
filter(sex=="F")
#t.test for difference in mean of predicted grades for males with and without ST present
#null hypothesis - mean of predicted grades is equals the mean of actual grades
t.test(PredictedGrade ~ STPresent, data= f_performance, alternative = c("two.sided"), conf.level = 0.95)
```
Both tests have a p-value higher than 0.05 denoting that neither gender experienced a statistically significant difference in predicted average grades based on exposure to stereotype activation or not. Further rejecting hypothesis one.
### H2. *Was there a statistically significant difference between predicted male and female achievement based on the type of stereotype activation?*
The graph below calculates the mean predicted grade for both groups based on the type of stereotype activation.
```{r, mean of predicted v. actual grades}
performance%>%
group_by(sex, StereotypeActivation)%>%
summarise(mean(PredictedGrade), mean(G3), mean(PredictedGrade)-mean(G3))
```
In the summary above, participants ranked the average predicted scores higher overall than the actual scores irrespective of gender or stereotype activation. The difference in predicted versus actual score was greatest among female students. Here participants exposed to the stereotype statistics predicted the widest difference compared to actual scores (2.47) and the highest overall scores (14.5).
For male students, predictions were closer to the average actual performance (11.80) ranging at a difference of 0.16 - 0.88 points. With no stereotype activation, males students garnered their highest predicted average at 12.68 suggesting introducing stereotypes negatively affected predictions in male students although still higher than actual performance. For female students, introducing statistics of lower male performance than females garnered the highest grade prediction for female students. For both genders, case based stereotype activation which included one example of a high female score and two examples of lower male scores produced the lowest predicted grades.
```{r, pairwise}
pairwise.t.test(x= performance$PredictedGrade, g=performance$StereotypeActivation, p.adjust.method = "none")
```
This may suggest that other variables in the study have an influential role in predicting scores outside of stereotype activation.
## Model Comparison
### Model 1 - Predicted Grades and Presence of Stereotype Activation
In the first model, I will use PredictedGrade as the outcome or dependent variable and the STPresent variable as the explanatory or independent variable adding in student sex as an interaction term.
```{r, model 1}
model1<- (lm(PredictedGrade ~ STPresent * sex, data=performance))
summary(model1)
```
Here we find in the absence of stereotype activation, gender is a statistically significant predictor of grades as represented by p-values under 0.05 and higher p-values when ST is present. However, the overall model of presence of stereotype activation and gender are not significant in predicting grades with a p-value of 2.17. This model confirms earlier hypothesis testing results that mean predicted grades based on ST is not as significant but gender may play a role.
### Model 2 and 3 - Predicted Grades by Stereotype Activation and Gender
The next two models address the second hypothesis and distinguishes the stereotype activation by type, adding the sex variable as both a second explanatory variable (model 2) and an interaction term (model 3).
```{r, model 2 and 3}
#model2 uses "sex" as explanatory variable
model2<-(lm(PredictedGrade ~ StereotypeActivation + sex, data=performance))
summary(model2)
#model3 uses "sex" as interaction terms
model3<- lm(PredictedGrade ~ StereotypeActivation * sex, data=performance)
summary(model3)
#ANOVA of both models
anova(model2, model3)
```
In both models, there is a significance to introducing case based ST for both genders, negatively for male students and positively for female students. The use of statistics garnered less significance for both genders, however still significant for predicting mean grades for female students. Once again the highest predicted scores for males were under conditions when ST was not present.
Comparing the two models, results are similar and there is minimal increase in the R-squared (0.053 to 0.056) and adjusted R-squared (0.050 to 0.051) for using sex as an explanatory variable vs. an interaction term. Residuals are also lower in model 3 than for model 2. The analysis of variance for the two models also confirms this result with lower RSS for model 3, minimizing residuals in the model. Thus model 3 is a better fit than model two.
### Model 4 - Predicted Grades by Other Potential Explanatory Variables
Until now, I investigated stereotype activation as the primary explanatory variable in predicting grades for both genders. However, in both my hypothesis testing and previous models, this variable was not significant in comparing scores with or without the presence of stereotype activation. This next model explores which of the other variables could explain this phenomena including gender as an interaction term.
Variables selected for exploration include:
-Studytime - weekly study time is categorized as 1= less than 2 hours, 2= 2-5 hours and 3= 5+ hours\
-Freetime - free time after school group as 1 = low, 2= medium, 3 = high\
-Goout - how often a student goes out with friends where 1 is very low and 4 is very often\
-Absences - number of school absences 1 - 7 where 7 represents any absences equal to or above 7\
-Walc - weekend alcohol consumption\
-Parents_edu - the higher of original variables mother's edu and father's edu, where 4 = the highest level of education
```{r, summary other variables}
performance%>%
group_by(sex)%>%
summarise(mean(studytime), mean(freetime), mean(goout), mean(absences),mean(G3), mean(PredictedGrade))
```
The above tables summarize differences in the mean values for several variables of interest by gender. Here we see, female students score slightly higher in study time (2.07 vs. 1.7) and while lower in free time (2.07 vs, 2.3), goout (3 vs. 3.05), absences (2.7 vs. 2.9). These would suggest female students may have a higher predicted grade based on good practices which is proven by the actual grades in G3 (12.15 vs. 11.80). However, there is larger discrepancies in predicted rages (14.0 for females vs. 12.28 for males).
```{r, model 4}
#model other variables as possible explanatory variables
model4 <-lm(PredictedGrade ~ (studytime + freetime + Walc + goout + Parents_edu + absences) * sex, data=performance)
summary(model4)
anova(model3, model4)
#create matrix of model plots
par(mfrow = c(2,3)); plot(model4, which = 1:6)
```
In this final model, we find similar residuals to model 3 but a large increase in the R-squared (0.057 to 0.34), adjusted r-squared values (0.051 to 0.33) and F-statistic (10.12 on 5 to 33.9 on 13). Based on the p-values, we also note study time, weekly alcohol consumption, parents education, and number of absences as most significant in predicting mean grades. Female students scored slighly more favorably in each of these areas than male students accounting a slight increase in actual grades as well. Thus perhaps participants over-estimated these values in predicting grades.
Comparing model 4 to model 3 using analysis of variance, there is a significant reduction in RSS and increase in p-value significance suggesting the introduction of these behavioral variables as a better fit for predicting grades than the introduction of stereotype activation. Note that in diagnosis the model 4 there are issues in normality (see the Cook's distance and Residuals vs. Leverage plots) as well as heteroskedasticity (see the Scale-Location plot). Since further evaluation of these variables are outside of the scope of this project, I will select model 3 for diagnostics.
## Diagnostics
For this section, I will evaluate a few assumptions with model 3 which aimed to predict grades by the type of stereotype activation and the sex variable as an interaction term.
```{r, diagnostics model 3}
#create matrix of model plots
par(mfrow = c(2,3)); plot(model3, which = 1:6)
```
*Normality of Errors -* In the Normal Q-Q plot, most observations fall close to the line assuming normality. Using the Cook's Distance and Residuals vs. Leverage, we can assume residuals are mostly normal as well with the exception of observation #62 whose leverage makes it an influential observation.
*Linearity -* Viewing the Residuals vs. Fitted plot, we see a relatively straight and horizontal line suggesting the average residual for the fitted values are relatively similar. Note, there are three observations, #62, #348, and #742 that are identified as outliers.
*Equal Variance of Errors* - Although the Residuals vs. Fitted plot show a near equal variance of the error terms based on its straight and horizontal line, the Scale-Location plot shows a decreasing rather than flat trend as the fitted values increase.
## Summary
In summary, stereotype activation has some influence in predicting higher scores for certain groups under certain conditions but was not a statistically significant predictor in grades for either male or female students based on this experiment. In this study, stereotypes favored female students over male students. Where this stereotype was present for both case based and statistic stereotypes, there was an increase in female predicted scores versus when ST was absent. Predictions for male grades also benefited from a higher predicted score when ST was absent. This does suggest there is some bias introduced with stereotype activation but not enough to be statistically significant in predicting grades.
A more robust model for predicting grades (model 4) incorporated student behavioral factors such as study time, weekly alcohol consumption, and number of school absences as well demographic factors such as parents education. Future research should further investigate these variables as well as test the inverse of the stereotype which would favor male students. Overall, participants generally predicted grades higher for both genders compared to actual but the average predicted scores were not statistically significant based on stereotype activation.
#### Sources
Bedyńska, S., Krejtz, I. & Sedek, G. Chronic stereotype threat and mathematical achievement in age cohorts of secondary school girls: mediational role of working memory, and intellectual helplessness. Soc Psychol Educ 22, 321--335 (2019). https://doi.org/10.1007/s11218-019-09478-6
Bedyńska, S., Krejtz, I., Rycielski, P. et al. Stereotype threat as an antecedent to domain identification and achievement in language arts in boys: a cross-sectional study. Soc Psychol Educ 23, 755--771 (2020). https://doi.org/10.1007/s11218-020-09557-z
Booth MZ, Gerard JM. Self-esteem and academic achievement: a comparative study of adolescent students in England and the United States. Compare. 2011 Sep;41(5):629-648. doi: 10.1080/03057925.2011.566688
Cortez, P. and Silva, A. Using Data Mining to Predict Secondary School Student Performance. In A. Brito and J. Teixeira Eds., Proceedings of 5th FUture BUsiness TEChnology Conference (FUBUTEC 2008) pp. 5-12, Porto, Portugal, April, 2008, EUROSIS, ISBN 978-9077381-39-7
Ganley, C. M., Mingle, L. A., Ryan, A. M., Ryan, K., Vasilyeva, M., & Perry, M. (2013). An examination of stereotype threat effects on girls' mathematics performance. Developmental Psychology, 49(10), 1886--1897. https://doi.org/10.1037/a0031412
Hyde, Janet Shibley. "Meta-analysis and the psychology of gender differences." Signs: Journal of Women in Culture and Society 16.1 (1990): 55-73.
Johnson, H., Barnard-Brak, L., Saxon, T., & Johnson, M.K. (2012) An Experimental Study of the Effects of Stereotype Threat and Stereotype Lift on Men and Women's Performance in Mathematics, The Journal of Experimental Education, 80:2, 137-149, DOI: 10.1080/00220973.2011.567312
Moè, A., & Putwain, D. W. (2020). An evaluative message fosters mathematics performance in male students but decreases intrinsic motivation in female students. Educational Psychology, 1--20. https://doi.org/10.1080/01443410.2020.1730767
Spinath, B., Harald Freudenthaler, H., & Neubauer, A. C. (2010). Domain-specific school achievement in boys and girls as predicted by intelligence, personality and motivation. Personality and Individual Differences, 48(4), 481-486. https://doi.org/10.1016/j.paid.2009.11.028
Steele, Claude M., and Joshua Aronson. "Stereotype threat and the intellectual test performance of African Americans." Journal of personality and social psychology 69.5 (1995): 797.
Warne, R. T. (2022). No Strong Evidence of Stereotype Threat in Females: A Reassessment of the Meta-Analysis. Journal of Advanced Academics, 33(2), 171--186. https://doi.org/10.1177/1932202X211061517
Data source: Anonymous. (2022). Performance vs. Predicted Performance\[Data set\]. Kaggle. https://doi.org/10.34740/KAGGLE/DSV/4282405