Code
library(tidyverse)
library(dplyr)
library(readxl)
library (ggplot2)
lungcap<- read_excel("_data/LungCapData.xls")
knitr::opts_chunk$set(echo = TRUE)Kalimah Muhammad
October 3, 2022
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.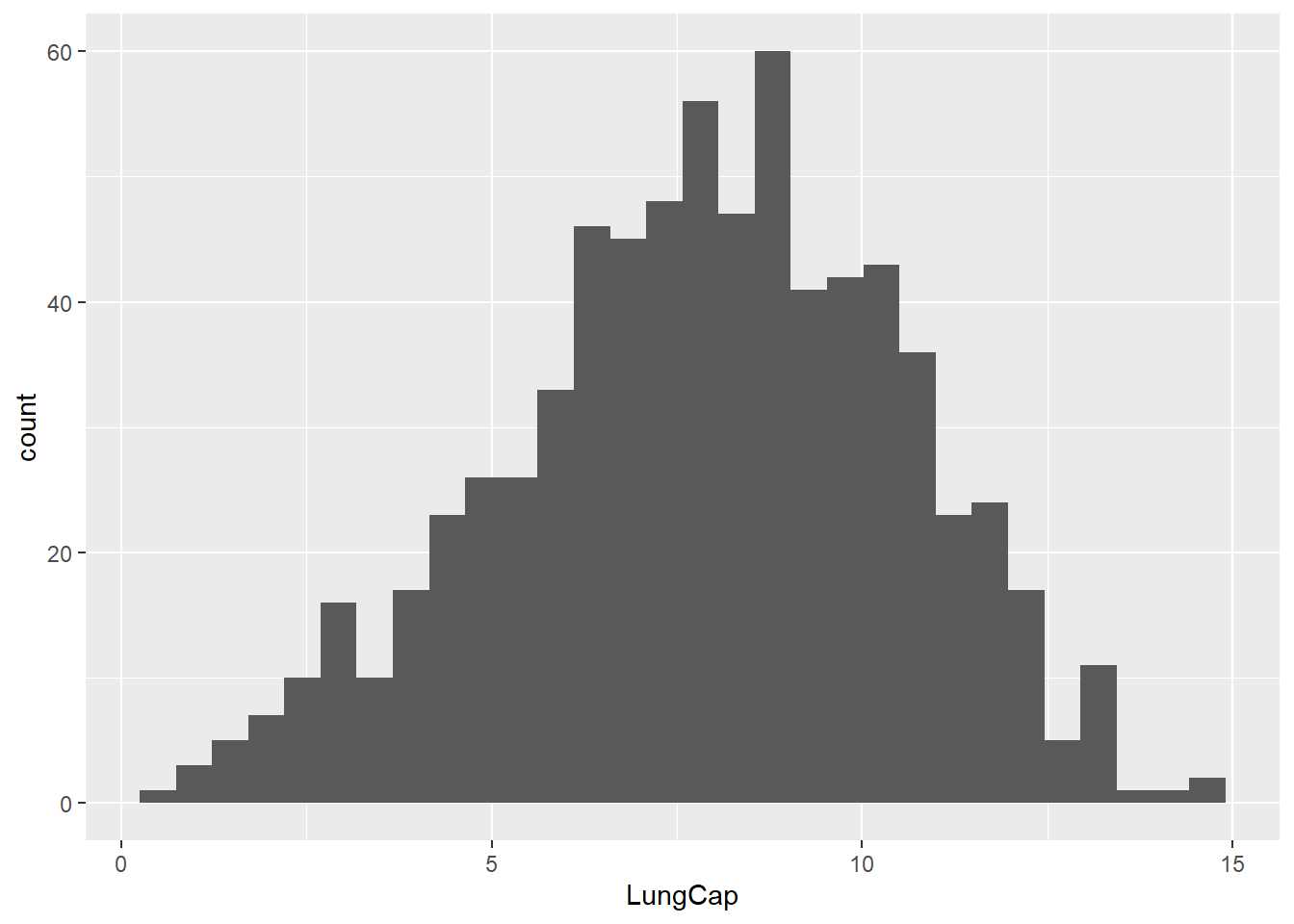
This is not normally distributed as there are far more observations of lower lung capacity than higher suggesting the distribution is negatively skewed.
# A tibble: 2 × 2
Gender `mean(LungCap)`
<chr> <dbl>
1 female 7.41
2 male 8.31The average lung capacity for females is 7.41, lower than the average for males at 8.31.
# A tibble: 2 × 2
Smoke `mean(LungCap)`
<chr> <dbl>
1 no 7.77
2 yes 8.65The mean lung capacity for non-smokers is 7.77, lower than the mean for smokers at 8.65. At first glance, this seems contradictory as one would guess smokers to have a lower lung capacity than non-smokers.The following grid displays non-smokers as having overall higher lung capacity, conflicting with the mean above.
# A tibble: 2 × 2
Smoke LungCap
<chr> <dbl>
1 no 6.36
2 yes 7.20# A tibble: 2 × 2
Smoke `mean(LungCap)`
<chr> <dbl>
1 no 9.14
2 yes 8.39# A tibble: 2 × 2
Smoke `mean(LungCap)`
<chr> <dbl>
1 no 10.1
2 yes 8.90# A tibble: 2 × 2
Smoke `mean(LungCap)`
<chr> <dbl>
1 no 11.1
2 yes 10.5With the exception of those age 13 years old and under, all non-smokers had a greater lung capacity than smokers. For those over the age of 18, the difference of the average in lung capacity for non-smokers to smokers was 0.55. For 16-17 year olds, the difference was the greatest at 1.16. The difference for 14-15 year olds was 0.74 and for those 13 years old and under, the difference was -0.843.
Here the average lung capacity for non-smokers is higher than for smokers. This differs from the results of question 1c. Overall, we see lung capacity increase with age irrespective of smoking so this may contribute to the change in results.
[1] 8.738289[1] 0.8196749The covariance between lung capacity and age is 8.74 suggesting a positive relationship in which both variables move in the same direction (i.e. for this data set an increase in lung capacity would suggest an increase in age as well).
The correlation between lung capacity and age is 0.82 suggesting a strong positive correlation (0.82 of a potential -1 to +1).
2a. What is the probability that a randomly selected inmate has exactly 2 prior convictions? 20%
2b. What is the probability that a randomly selected inmate has fewer than 2 prior convictions? 69%
2c. What is the probability that a randomly selected inmate has 2 or fewer prior convictions? 89%
2d. What is the probability that a randomly selected inmate has more than 2 prior convictions? 11%
2e. What is the expected value for the number of prior convictions?
2f. Calculate the variance and the standard deviation for the Prior Convictions.
---
title: 'Resubmission: Homework #1'
author: "Kalimah Muhammad"
date: "10/03/2022"
desription: "Descriptive Statistics"
format:
html:
toc: true
code-fold: true
code-copy: true
code-tools: true
categories:
- hw1
- Kalimah Muhammad
---
```{r}
#| label: setup
#| warning: false
library(tidyverse)
library(dplyr)
library(readxl)
library (ggplot2)
lungcap<- read_excel("_data/LungCapData.xls")
knitr::opts_chunk$set(echo = TRUE)
```
## LungCapData
### 1a. What does the distribution of LungCap look like?
```{r}
ggplot(lungcap, aes(x=LungCap))+ geom_histogram()
```
This is not normally distributed as there are far more observations of lower lung capacity than higher suggesting the distribution is negatively skewed.
### 1b. Compare the probability distribution of the LungCap with respect to Males and Females?
```{r}
lungcap %>%
group_by(Gender)%>%
summarise(mean(LungCap))
```
The average lung capacity for females is 7.41, lower than the average for males at 8.31.
### 1c. Compare the mean lung capacities for smokers and non-smokers. Does it make sense?
```{r}
lungcap %>%
group_by(Smoke)%>%
summarise(mean(LungCap))
```
The mean lung capacity for non-smokers is 7.77, lower than the mean for smokers at 8.65. At first glance, this seems contradictory as one would guess smokers to have a lower lung capacity than non-smokers.The following grid displays non-smokers as having overall higher lung capacity, conflicting with the mean above.
```{r}
ggplot(lungcap, aes(x = LungCap)) +
facet_grid(Gender ~ Smoke)+
geom_histogram()
```
### 1d. Examine the relationship between Smoking and Lung Capacity within age groups: “less than or equal to 13”, “14 to 15”, “16 to 17”, and “greater than or equal to 18”.
```{r}
#Lung capacity for those age 13 and under
lungcap %>%
filter(Age <= 13)%>%
group_by(Smoke)%>%
summarise(LungCap = mean(LungCap))
#Lung capacity for those between the age of 14 to 15
lungcap%>%
filter(Age== 14 | Age ==15)%>%
group_by(Smoke)%>%
summarise(mean(LungCap))
#Lung capacity for those between the age of 16 to 17
lungcap%>%
filter(Age==16 |Age==16)%>%
group_by(Smoke)%>%
summarise(mean(LungCap))
#Lung capacity for those 18 and older
lungcap%>%
filter(Age>=18)%>%
group_by(Smoke)%>%
summarise(mean(LungCap))
```
### 1e. Compare the lung capacities for smokers and non-smokers within each age group.
With the exception of those age 13 years old and under, all non-smokers had a greater lung capacity than smokers. For those over the age of 18, the difference of the average in lung capacity for non-smokers to smokers was 0.55. For 16-17 year olds, the difference was the greatest at 1.16. The difference for 14-15 year olds was 0.74 and for those 13 years old and under, the difference was -0.843.
### Is your answer different from the one in part c? What could possibly be going on here?
Here the average lung capacity for non-smokers is higher than for smokers. This differs from the results of question 1c. Overall, we see lung capacity increase with age irrespective of smoking so this may contribute to the change in results.
### 1f. Calculate the correlation and covariance between Lung Capacity and Age. (use the cov() and cor() functions in R). Interpret results.
```{r}
cov(lungcap$LungCap, lungcap$Age)
cor(lungcap$LungCap, lungcap$Age)
```
The covariance between lung capacity and age is 8.74 suggesting a positive relationship in which both variables move in the same direction (i.e. for this data set an increase in lung capacity would suggest an increase in age as well).
The correlation between lung capacity and age is 0.82 suggesting a strong positive correlation (0.82 of a potential -1 to +1).
## Inmate Data
```{r}
priors<- c(0, 1, 2, 3, 4)
frequency<- c(128, 434, 160, 64, 24)
prison <-data.frame(priors,frequency)
View(prison)
```
2a. What is the probability that a randomly selected inmate has exactly 2 prior convictions? 20%
2b. What is the probability that a randomly selected inmate has fewer than 2 prior convictions? 69%
2c. What is the probability that a randomly selected inmate has 2 or fewer prior convictions? 89%
2d. What is the probability that a randomly selected inmate has more than 2 prior convictions? 11%
2e. What is the expected value for the number of prior convictions?
```{r}
((128*0)+(434*1)+(160*2)+(64*3)+(24*4))/sum(frequency)
```
2f. Calculate the variance and the standard deviation for the Prior Convictions.
```{r}
var(prison$priors)*((810-1)/810)#calculate population variance
sd(prison$priors)
```