Homework #3

hw3

Kalimah Muhammad

Author

Kalimah Muhammad

Published

October 31, 2022

Code

library(tidyverse)
library(dplyr)
library(ggplot2)
library(alr4)
library(smss)
knitr::opts_chunk$set(echo = TRUE)

Question 1: United Nations

Code

data(UN11) #load United Nations data

1.1.1

The predictor variable is ppgdp (the gross national product per person in USD) and the response or outcome variable in fertility (the birth rate per 1000 females).

1.1.2

Code

ggplot(UN11, aes(x=ppgdp, y=fertility))+ geom_point()

Fertility has the most variability at zero gross national product per person (ppgdp) where countries range from birthrate of 1 to 7 per 1000 females. There is a sharp decline thereafter where the fertility rate is consistently 3 or under and hovers between slightly above 2 and 1 for countries with a ppgdp above 30,000.

Code

plot(x=UN11$ppgdp, y=UN11$fertility)

Based on the plot above, there is little difference between the two plots.

1.1.3.

Code

plot(x= log(UN11$ppgdp), y=UN11$fertility)

Using natural logarithms, the model seems more plausible as the data becomes normalized.

Question 2: Annual Income

2a.

When the British pound is used instead of the dollar, the steep of the slop minimizes.

2b.

THe correlation does not change when factoring in pound in lieu of the dollar.

Question 3: Water runoff in the Sierras

Using the pairwise scatterplot, we find some pairs are better represented by a straight line than others. This seems to be common among mountain ranges with similar starting initials (i.e. of the ranges starting with “A” or those starting with “O”).In each case, those pairs have a clear positive slope. Examining the percipitation by year and mountain range shows a wide range of variability with a singular outlier for each mountain range.

Code

data(water) #load water data
pairs(water) #plot pairs

Code

fit_water <- lm(Year~APMAM+ APSAB+ APSLAKE+ OPBPC+ OPRC+ OPSLAKE+ BSAAM, data=water) #create linear regression model based on year and mountain range
summary(fit_water) #summarize model


Call:
lm(formula = Year ~ APMAM + APSAB + APSLAKE + OPBPC + OPRC + 
    OPSLAKE + BSAAM, data = water)

Residuals:
    Min      1Q  Median      3Q     Max 
-20.135  -7.762  -1.500   8.473  27.092 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.962e+03  7.979e+00 245.831   <2e-16 ***
APMAM       -1.256e+00  1.158e+00  -1.084    0.286    
APSAB       -7.327e-01  2.494e+00  -0.294    0.771    
APSLAKE      2.351e+00  2.276e+00   1.033    0.309    
OPBPC       -7.900e-02  7.543e-01  -0.105    0.917    
OPRC        -1.975e+00  1.170e+00  -1.687    0.100    
OPSLAKE      5.219e-01  1.369e+00   0.381    0.705    
BSAAM        3.353e-04  2.722e-04   1.232    0.226    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 12.34 on 35 degrees of freedom
Multiple R-squared:  0.1949,    Adjusted R-squared:  0.03388 
F-statistic:  1.21 on 7 and 35 DF,  p-value: 0.3231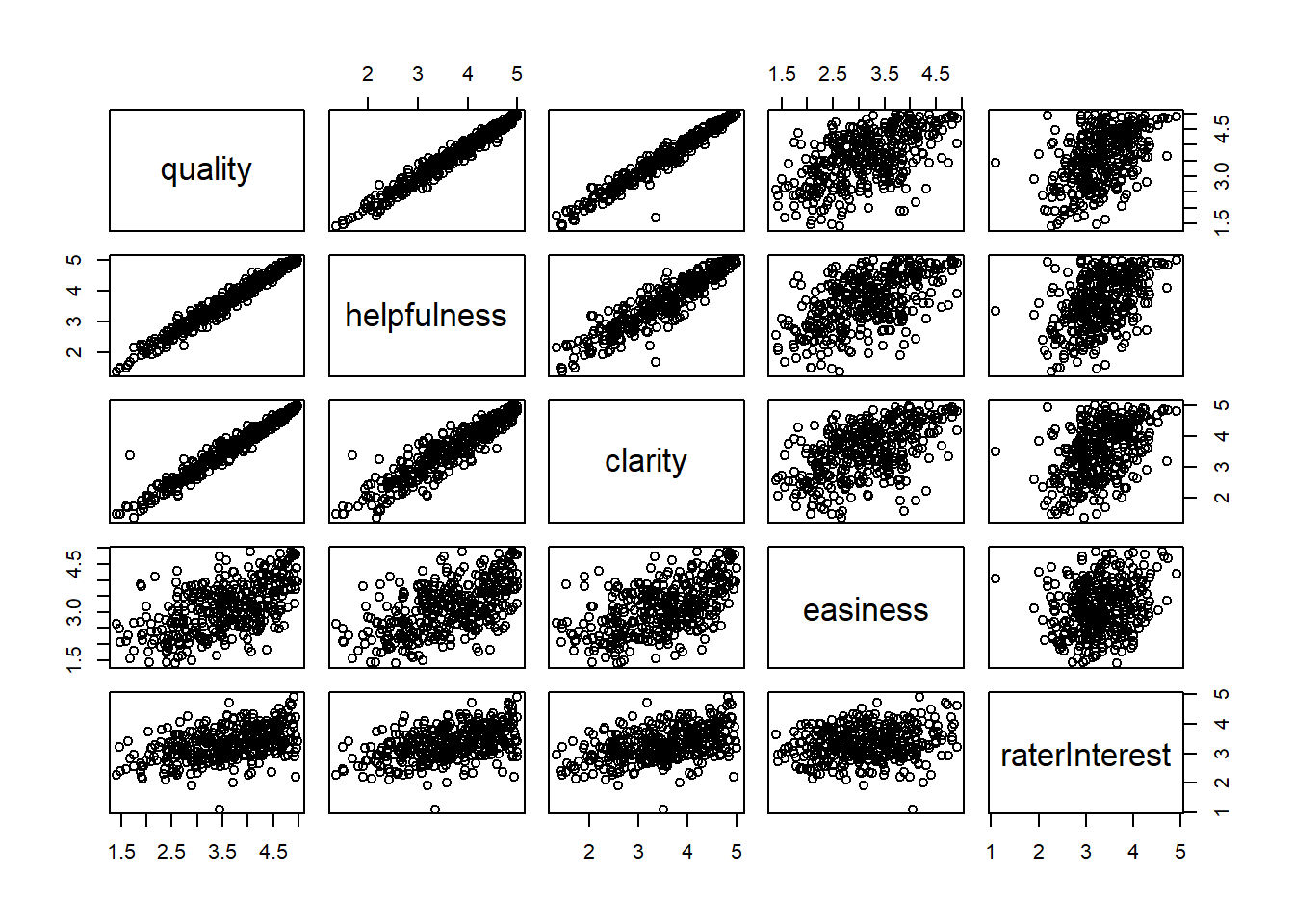

Question 4: Professor ratings

Code

data("Rateprof") #load data
Rateprof%>%
  select(quality, helpfulness, clarity, easiness, raterInterest)%>%
pairs()

Based on the scatterplot, quality appears to be positive related to helpfulness and clarity. There’s more variablity in results for easiness and aterInterest.

Question 5: Student Survey

Code

data("student.survey")
fit_smss<- lm(factor(pi) ~ re, data = student.survey)

Warning in model.response(mf, "numeric"): using type = "numeric" with a factor
response will be ignored

Warning in Ops.ordered(y, z$residuals): '-' is not meaningful for ordered
factors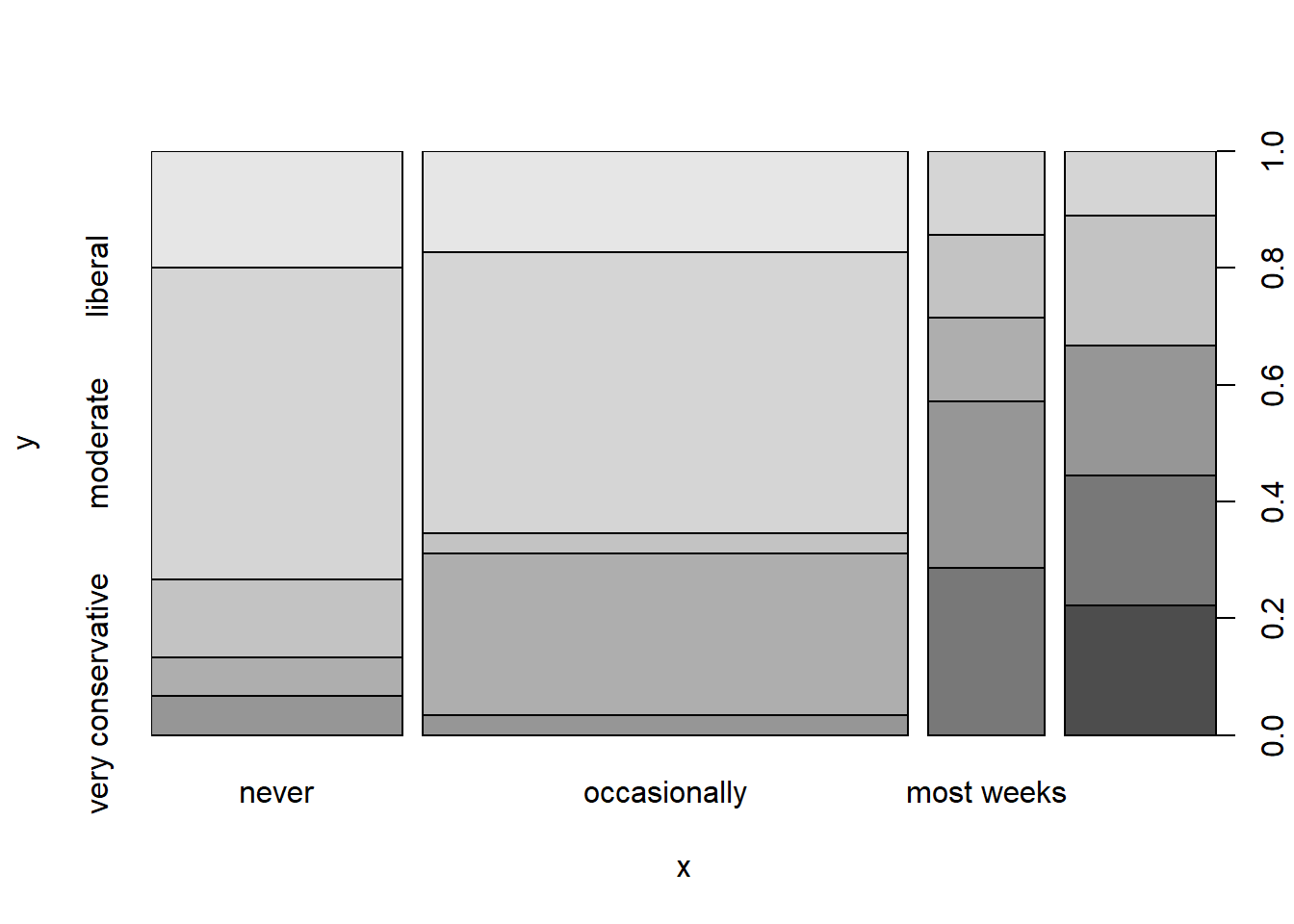

Code

plot(x=student.survey$re, y=student.survey$pi)

Code

fit_smss2<- lm(tv ~ hi, data = student.survey)
summary(fit_smss2)


Call:
lm(formula = tv ~ hi, data = student.survey)

Residuals:
   Min     1Q Median     3Q    Max 
-8.600 -3.790 -1.167  2.408 27.746 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)   20.200      6.175   3.271   0.0018 **
hi            -3.909      1.849  -2.114   0.0388 * 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.528 on 58 degrees of freedom
Multiple R-squared:  0.07156,   Adjusted R-squared:  0.05555 
F-statistic: 4.471 on 1 and 58 DF,  p-value: 0.03879

Code

plot(x=student.survey$hi, y=student.survey$tv)

The summary above shows there is a statistically signifcate relationship between high school GPA and the number of TV hours watched per week.