Code
library(tidyverse)
library(ggplot2)
library(treemap)
knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)Srujan Kagitala
July 4, 2023
For my final project, I would do exploratory analysis on the Olympics data right from the year it started in 1896 in Athena till 2016 in Rio de Janeiro.
Olympics is the most decorated sporting event in an athlete’s career. The Olympics are the leading international sporting events featuring summer and winter sports competitions in which thousands of athletes from around the world participate in a variety of competitions. The Olympic Games are considered the world’s foremost sports competition with more than 200 teams, representing sovereign states and territories, participating. The Olympic Games are normally held every four years, and since 1994, have alternated between the Summer and Winter Olympics every two years during the four-year period. The first, second, and third place finishers in each event receive Olympic medals: gold, silver, and bronze, respectively.
The dataset I would use for this analysis is downloaded from Kaggle.
This dataset consists of Olympics data of over a century, from the year 1896 to 2016. Studying this dataset will help to understand the patterns followed in the games of Olympics, patterns of the most successful athletes and countries in their Olympics journey and much more!
The data set has 271116 observations and 15 data points recorded per observation. Each observation records variables like ID, Name, Sex, Age, Height, Weight, Team, NOC, Games, Year, Season, City, Sport, Event, Medal.
The youngest and the oldest athlete that ever participated are 10 and 97 years of age respectively. Athletes from across the world compete in 765 events that happen across 66 sports. These happen in 2 Olympic seasons i.e Summer, Winter.
The dataset is mostly clean and we don’t have to work around much. Although, for doing some analysis, we might need to create various subsets of data like medals, teams, etc, drop na values for a few variables and mutate new variables(Most of these can be done during the analysis). We need to convert categorical variables into factor to get overall summary across various variables. We don’t need the “ID” column for our analysis as it only serves the purpose of a key.
Name Sex Age Height
Robert Tait McKenzie : 58 F: 74522 Min. :10.00 Min. :127.0
Heikki Ilmari Savolainen: 39 M:196594 1st Qu.:21.00 1st Qu.:168.0
Joseph "Josy" Stoffel : 38 Median :24.00 Median :175.0
Ioannis Theofilakis : 36 Mean :25.56 Mean :175.3
Takashi Ono : 33 3rd Qu.:28.00 3rd Qu.:183.0
Alexandros Theofilakis : 32 Max. :97.00 Max. :226.0
(Other) :270880 NA's :9474 NA's :60171
Weight Team NOC Games
Min. : 25.0 United States: 17847 USA : 18853 2000 Summer: 13821
1st Qu.: 60.0 France : 11988 FRA : 12758 1996 Summer: 13780
Median : 70.0 Great Britain: 11404 GBR : 12256 2016 Summer: 13688
Mean : 70.7 Italy : 10260 ITA : 10715 2008 Summer: 13602
3rd Qu.: 79.0 Germany : 9326 GER : 9830 2004 Summer: 13443
Max. :214.0 Canada : 9279 CAN : 9733 1992 Summer: 12977
NA's :62875 (Other) :201012 (Other):196971 (Other) :189805
Year Season City Sport
Min. :1896 Summer:222552 London : 22426 Athletics : 38624
1st Qu.:1960 Winter: 48564 Athina : 15556 Gymnastics: 26707
Median :1988 Sydney : 13821 Swimming : 23195
Mean :1978 Atlanta : 13780 Shooting : 11448
3rd Qu.:2002 Rio de Janeiro: 13688 Cycling : 10859
Max. :2016 Beijing : 13602 Fencing : 10735
(Other) :178243 (Other) :149548
Event Medal
Football Men's Football : 5733 Bronze: 13295
Ice Hockey Men's Ice Hockey : 4762 Gold : 13372
Hockey Men's Hockey : 3958 Silver: 13116
Water Polo Men's Water Polo : 3358 NA's :231333
Basketball Men's Basketball : 3280
Cycling Men's Road Race, Individual: 2947
(Other) :247078 #Type of medals won by teams.
teams_medals_type <- medals %>%
group_by(NOC, Medal) %>%
summarise(count = n())
#Total medals won by teams
teams_medals_total <- medals %>%
group_by(NOC) %>%
summarise(total_medals = n()) %>%
arrange(desc(total_medals))
#Top 50 countries(by total medals won) medal_type tally.
(teams_medals_tally <- inner_join(teams_medals_type,
teams_medals_total[1:50, ],
by = "NOC") %>%
arrange(desc(total_medals)))#Bar plot of medals won by top 50 countries.
ggplot(data = teams_medals_tally , aes(x= reorder(NOC, total_medals), y = count)) +
geom_bar(stat = "identity",
mapping = aes(fill = Medal),
position = "stack") +
labs(title ="Top 50 countries that won most medals",
y = "No of medals",
x = "Nation of Origin",
fill = "Medal")+
coord_flip()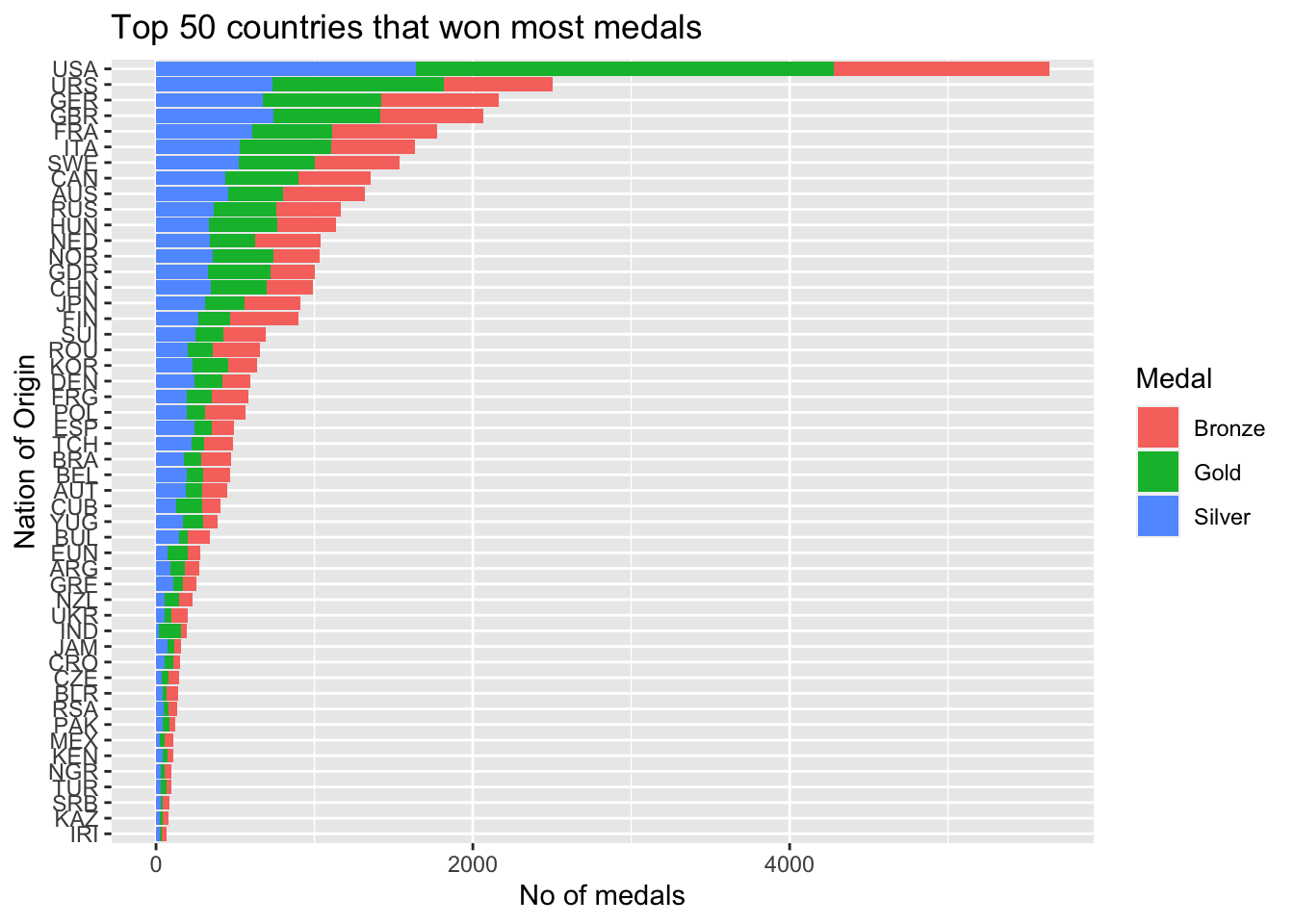
We can see that USA has won the highest number of medals, more than double the number of medals won by Soviet Union.
#Treemap representing each Sport proportional to number of events in olympics
treemap(sport_events,
index = "Sport",
vSize = "no_events",
type = "index",
fontsize.labels = 10,
fontcolor.labels = "black",
align.labels=list(
c("center", "center")),
inflate.labels=F,
palette = "Set1",
title="Treemap representing each Sport proportional to number of events in olympics",
fontsize.title=12)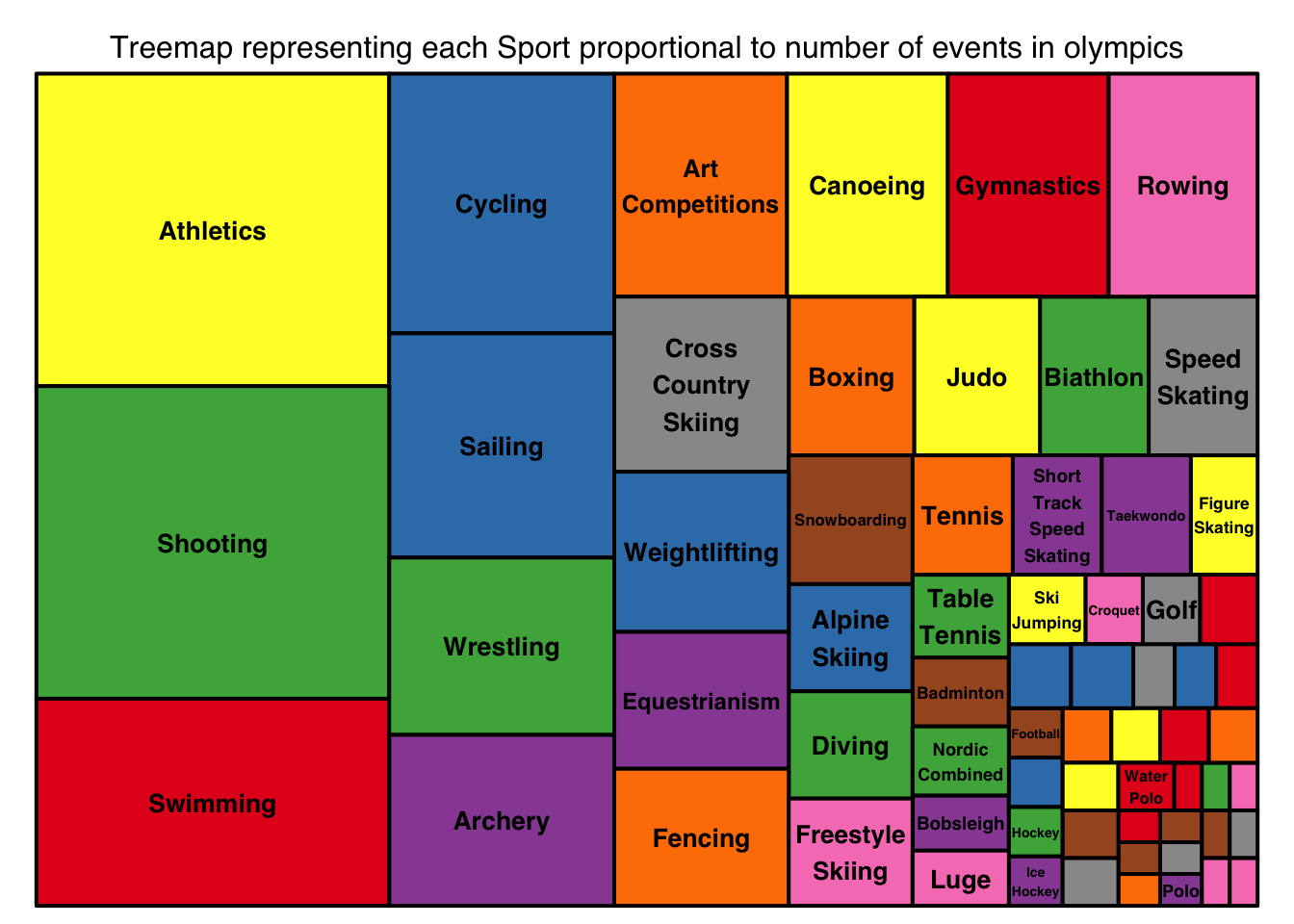
Athletics and shooting are the sports with highest number of events (83 events each) followed by swimming with 55 events.
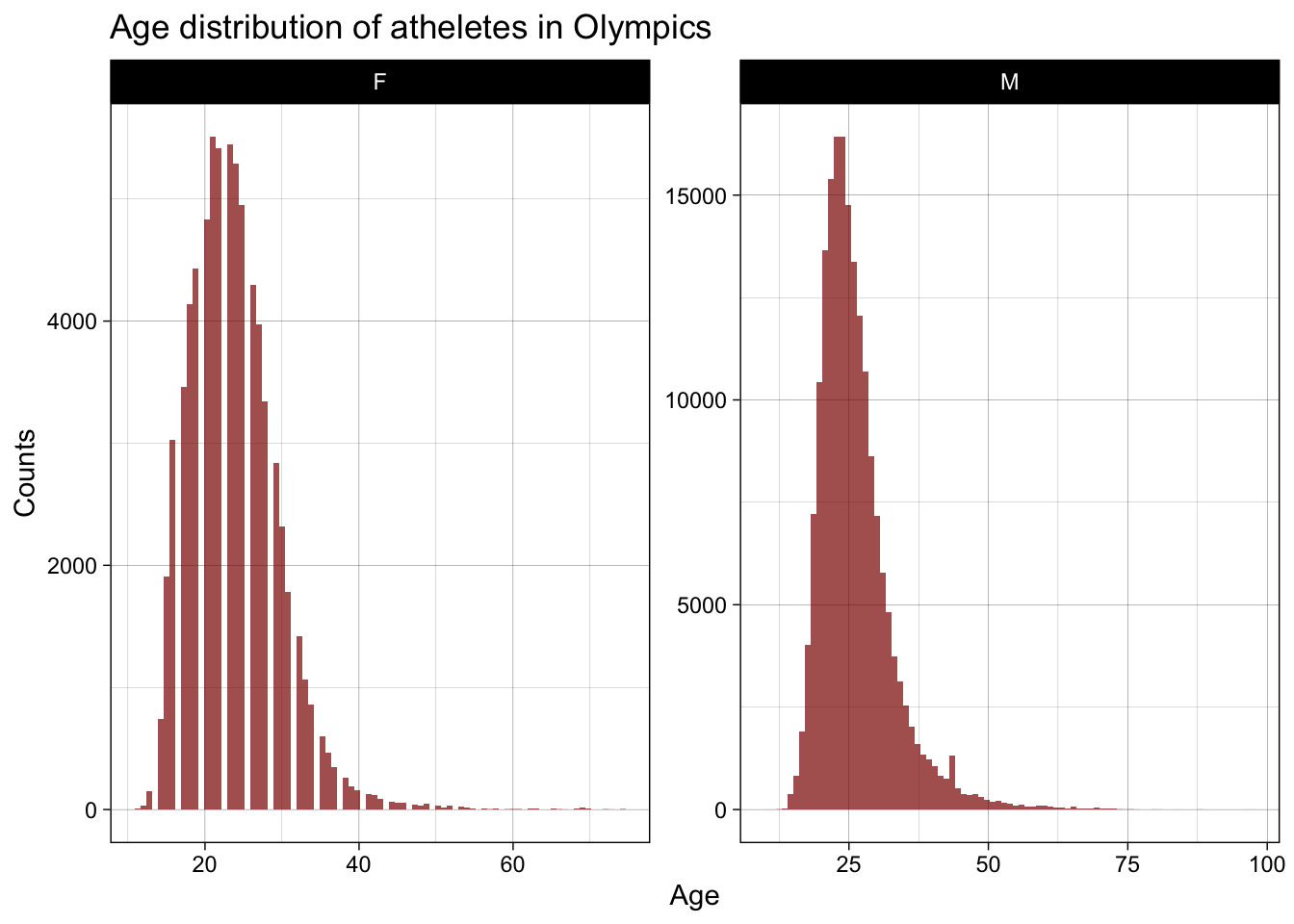
We can see that the mean age of men athletes is higher than the mean age of women athletes. Most frequent age in men athletes is approximately equal to the most frequent age in women athletes.
#Times series for how top 10 nations performed over years.
teams_medals_yearly <- medals %>%
filter(NOC %in% teams_medals_total[1:9,]$NOC) %>%
group_by(NOC, Year) %>%
summarise(total_medals = n()) %>%
arrange(NOC,Year)
ggplot(teams_medals_yearly,
aes(x= Year, y = total_medals)) +
geom_line(color = "darkgreen") +
facet_wrap(~NOC, scales = "free") +
#scale_x_continuous(breaks = c(2015, 2016, 2017),
#labels = c("2015", "2016", "2017")) +
theme_linedraw()+
labs(title = "Medals won over years by top 10 countries since 1896",
x = "Year",
y = "Number of medals")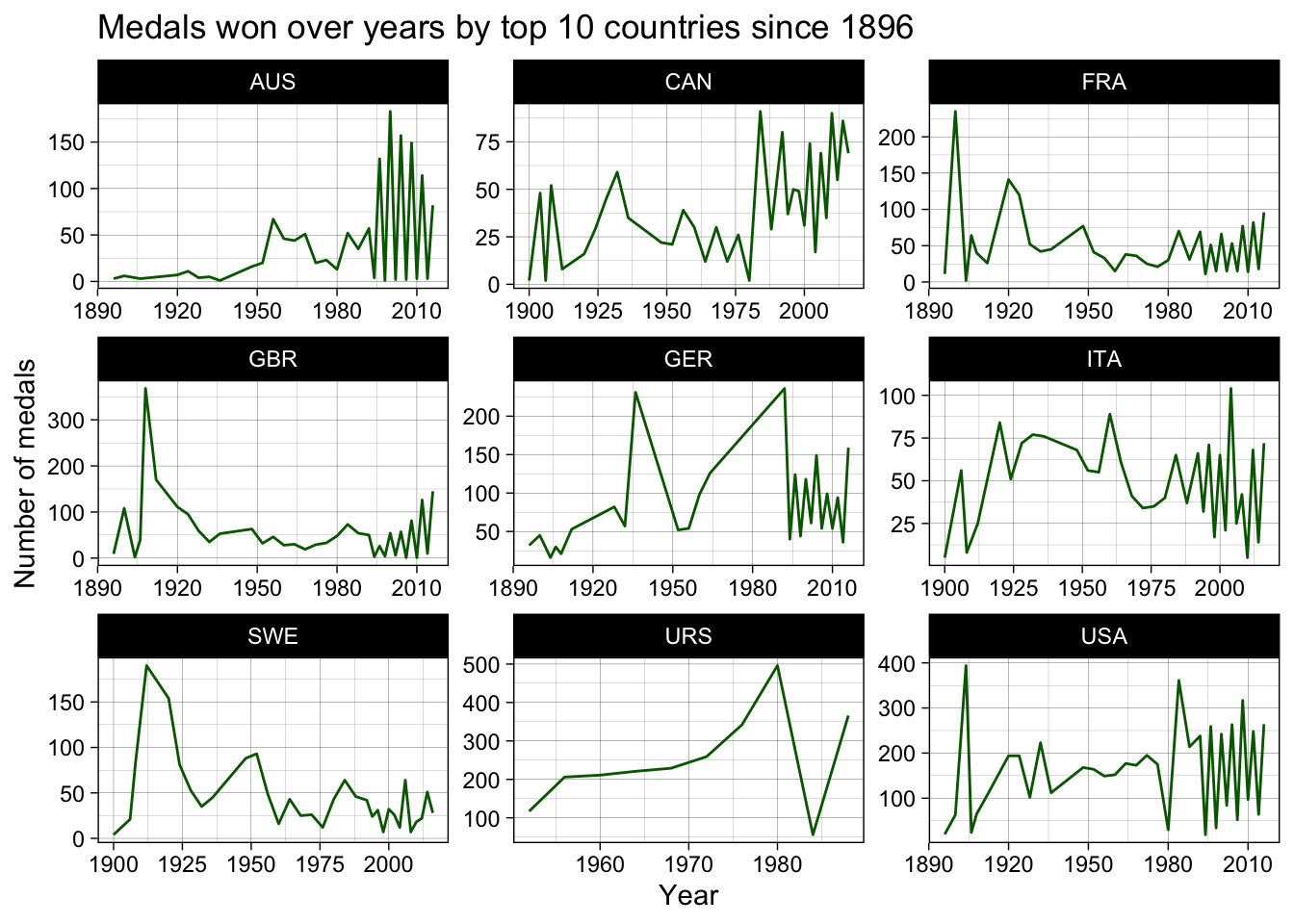
Is there an unbiased ranking system to determine the rankings of nations in Olympics? Can we rank different nations on varied ranking systems (different weightage for gold, silver and bronze) and observe how their ranks differ based on weightage given to gold, silver and bronze medals?
230 countries participated in Olympics since the start till the event in 2016. So, we will analyse how varied ranking systems for different years(approx two or three years) in which the number of countries participated is greater than 200 to ensure that we find an unbiased ranking system. We will use that system to rank nations for one random year and also over the years.
Design.
The total weighted medal values for each country determine the country’s rank in the Olympics. The weighted value of the medals won by a country is found by multiplying the number of gold, silver and bronze medals by their respective weight and then summing them. Bronze medals are always worth one point. Gold medals can’t be worth less than silver and silver can’t be worth less than bronze.
A ranking system is defined by silver multiplier and gold multiplier (bronze is always worth 1 point).The weighted value for silver in a ranking system is calculated by multiplying the number of silver medals by weight multiplier of silver. The weight for gold in a ranking system is calculated by multiplying the number of gold medals by weight multiplier of gold. Each country’s weighted medal values are summed for each medal. These totals are ranked in such a fashion that the lowest rank is allotted to the country with the highest weighted value.
Description of Ranking Systems used in the analysis. (Each system is defined by silver and gold multiplier)
I will verify the ranking systems for years 2016 and 2008.
(medals_2016 <- medals %>%
filter(Year == 2016) %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(system_1 = Gold + Silver + Bronze,
rank_1 = min_rank(-system_1),
system_2 = 5*Gold + 2*Silver + Bronze,
rank_2 = min_rank(-system_2),
system_3 = 5*Gold + 5*Silver + Bronze,
rank_3 = min_rank(-system_3),
system_4 = 10*Gold + 2*Silver + Bronze,
rank_4 = min_rank(-system_4),
system_5 = 10*Gold + 5*Silver + Bronze,
rank_5 = min_rank(-system_5),
system_6 = 20*Gold + 5*Silver + Bronze,
rank_6 = min_rank(-system_6),
system_7 = Gold,
rank_7 = min_rank(-system_7)) %>%
arrange(rank_1))ranks_2016 <- medals_2016 %>%
select(NOC, rank_1, rank_2, rank_3, rank_4, rank_5, rank_6, rank_7) %>%
arrange(rank_1) %>%
slice(1:50) %>%
pivot_longer(c("rank_1", "rank_2", "rank_3", "rank_4", "rank_5", "rank_6", "rank_7"),
names_to = "type",
values_to = "rank")
ggplot(ranks_2016, aes(x = type, y=NOC, label=rank, fill=rank)) +
geom_tile() +
geom_text(color = "white", size = 2)+
scale_fill_continuous(low = "darkorange",
high = "darkblue",
name = "rank") +
theme(axis.text.x = element_text(angle = 90),
axis.text.y = element_text(size = 6))+
labs(title = "Heatmap of rankings for top 50 total medal winning countries in 2016",
y = "Nation",
x = "Ranking System")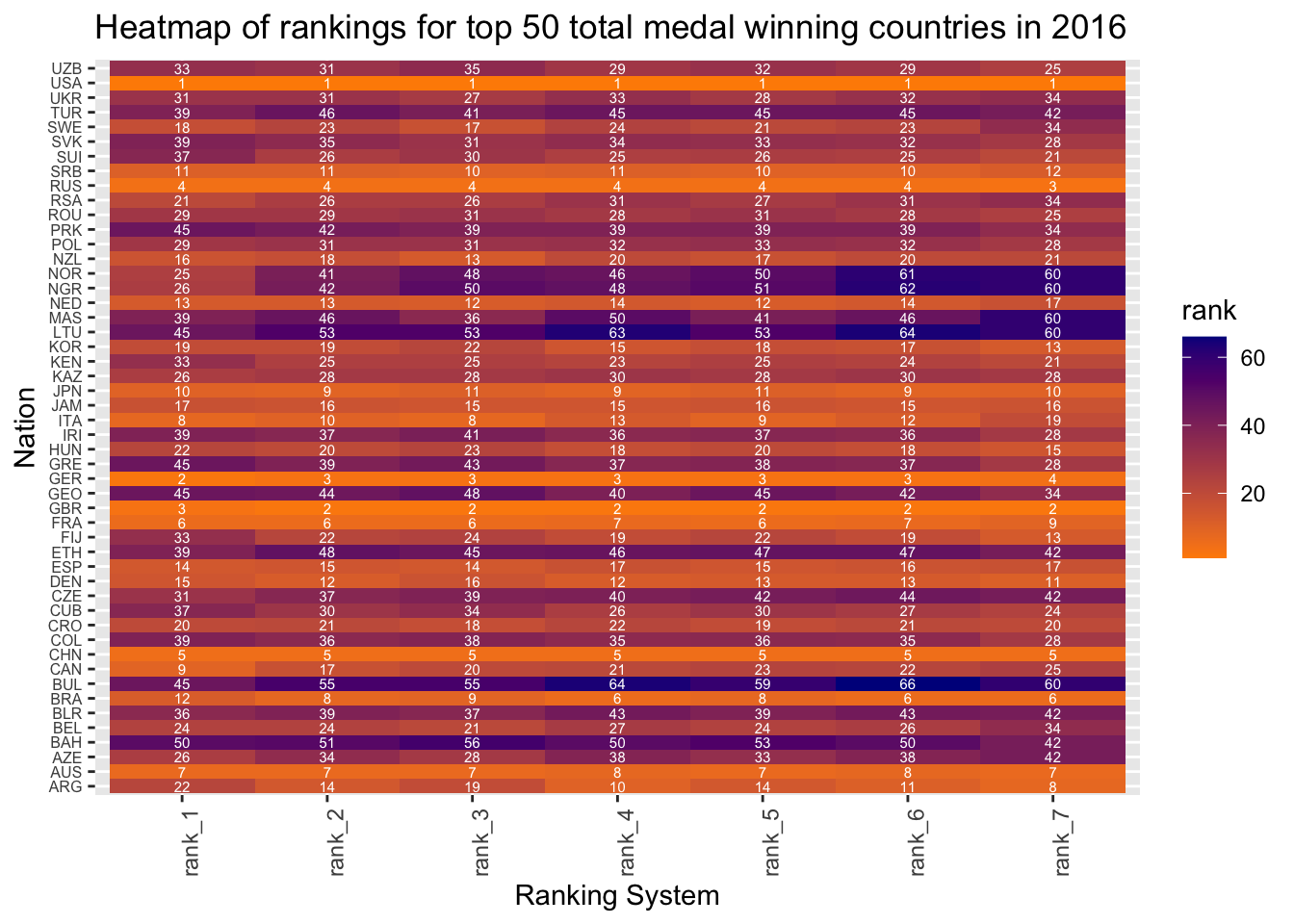
From the above heatmap of rankings for year 2016, we can see that, rank_5 has the least deviation from rankings by other systems for most of the countries. Also, rank_2 is fairly close to most of the other rankings. Hence, either of them can be used as the best estimator of country rankings for the year 2016. Likewise, let’s verify for year 2008 and see if there is a common best system for both the years.
(medals_2008 <- medals %>%
filter(Year == 2008) %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(system_1 = Gold + Silver + Bronze,
rank_1 = min_rank(-system_1),
system_2 = 5*Gold + 2*Silver + Bronze,
rank_2 = min_rank(-system_2),
system_3 = 5*Gold + 5*Silver + Bronze,
rank_3 = min_rank(-system_3),
system_4 = 10*Gold + 2*Silver + Bronze,
rank_4 = min_rank(-system_4),
system_5 = 10*Gold + 5*Silver + Bronze,
rank_5 = min_rank(-system_5),
system_6 = 20*Gold + 5*Silver + Bronze,
rank_6 = min_rank(-system_6),
system_7 = Gold,
rank_7 = min_rank(-system_7)) %>%
arrange(rank_1))ranks_2008 <- medals_2008 %>%
select(NOC, rank_1, rank_2, rank_3, rank_4, rank_5, rank_6, rank_7) %>%
arrange(rank_1) %>%
slice(1:50) %>%
pivot_longer(c("rank_1", "rank_2", "rank_3", "rank_4", "rank_5", "rank_6", "rank_7"),
names_to = "type",
values_to = "rank")
ggplot(ranks_2008, aes(x = type, y=NOC, label=rank, fill=rank)) +
geom_tile() +
geom_text(color = "white", size = 2)+
scale_fill_continuous(low = "darkorange",
high = "darkblue",
name = "rank") +
theme(axis.text.x = element_text(angle = 90),
axis.text.y = element_text(size = 6))+
labs(title = "Heatmap of rankings for top 50 total medal winning countries in 2008",
y = "Nation",
x = "Ranking System")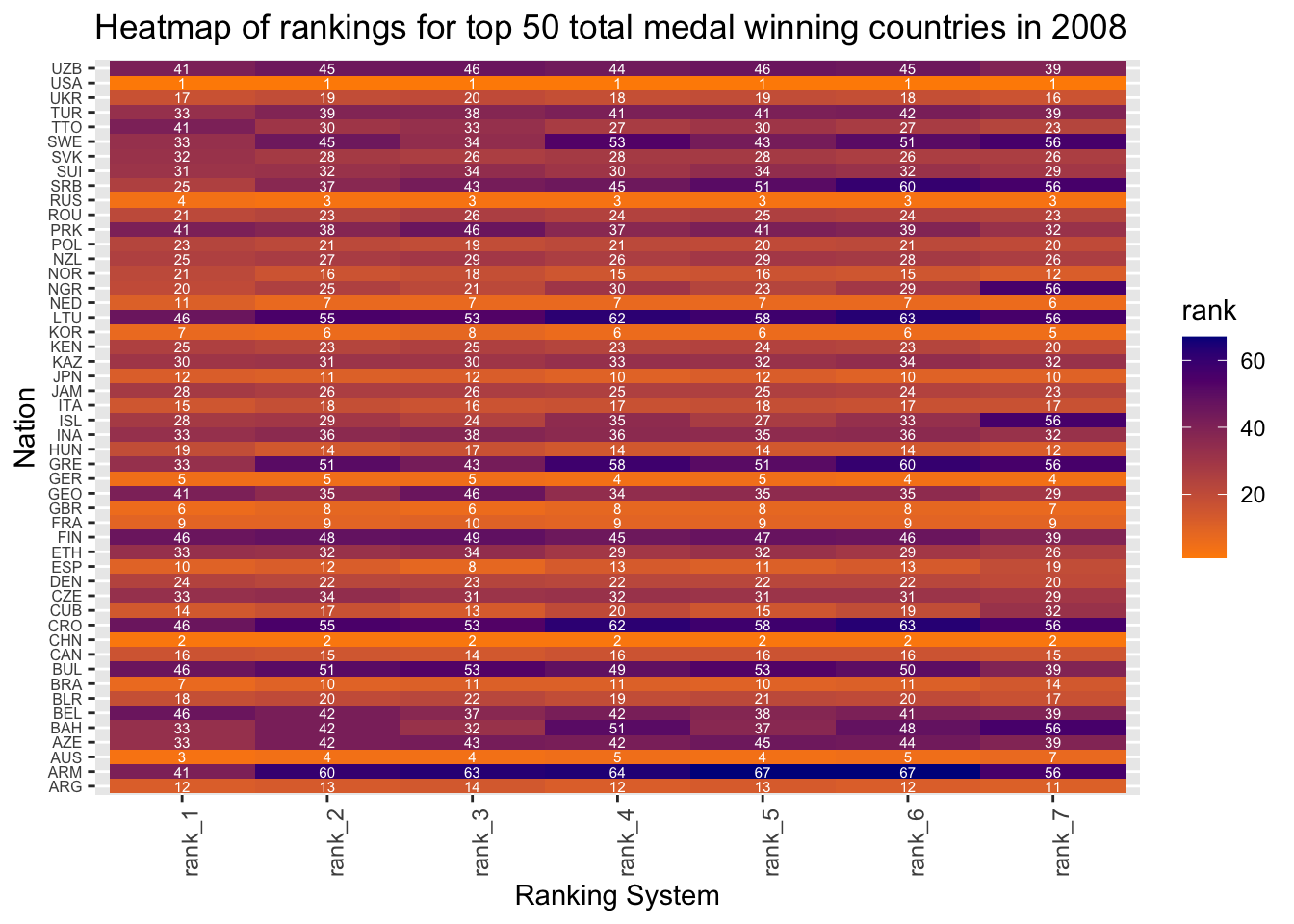
From the above heatmap of rankings for year 2008, we can see that, rank_5 has the least deviation from rankings by other systems for most of the countries. Also, rank_3 is fairly close to most of the other rankings. Hence, either of them can be used as the best estimators of country rankings for the year 2008.
Analysis on 2008 and 2016 showed that ranking system 5 has the least deviation from other rankings. So, we can use this as the best estimator for ranking nations. This might not be completely unbiased but it fairly ranks the countries according to the medals won.
Below table shows rankings of countries for the year 1912 using system 5.
Let’s see the overall rankings from 1896 to 2016 using ranking system 5. We will rank based on average_points per appearance. Total points is divided by number of appearances to eliminate bias (to some extent) that occurs from the fact that a few nations might take part more number of times compared to others. Only nations above 10th percentile of number of appearances are ranked because there could be outliers on the lower end (especially countries who participated only once).
medals_all_years <- medals %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(points = 10*Gold + 5*Silver + Bronze)
appearances <- olympics_data %>%
distinct(NOC, Year) %>%
group_by(NOC) %>%
summarise(no_appearances = n())
no_appearances_10p <- quantile(appearances$no_appearances, probs = 0.1)
appearances <- appearances %>%
filter(no_appearances > no_appearances_10p )
medals_all_years <- inner_join(medals_all_years,
appearances,
by = "NOC") %>%
mutate(avg_points_per_appearance = points/no_appearances,
rank = min_rank(-avg_points_per_appearance)) %>%
arrange(rank)
medals_all_yearsCan we identify the most decorated athlete of all time, most decorated men and women athlete?
First we compute the weighted value of medals (points) won by athletes across years using ranking system 5 (the best ranking system as shown previously). The most decorated athlete is definitely based on the number of points earned.
Another ranking system can be designed based on overall number of events the athlete has participated in years and the number of appearances over years. This can be defined as impact rankings. This system tries to give more weightage to points scored by athletes who scored comparable points in lesser time frames(either lesser appearances or lesser events). Impact ranking is based on extrapolated impact points. Impact points are calculated by using points, normalized number of events (normal_events) and normalized number of appearances(normal_years). Only athletes with number of events and number of appearances above 10th percentile are ranked because there could be outliers on the lower end (especially for those who either participated in a single event or only appeared once). \[ impact\_points = (points * normal\_events)/normal\_years \]
athletes_gender <- olympics_data %>%
distinct(Name, Sex) %>%
select(Name, Sex)
athlete_medals_all_years <- medals %>%
group_by(Name, Medal) %>%
summarise(count = n()) %>%
ungroup() %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(points = 10*Gold + 5*Silver + Bronze,
rank_decorated = min_rank(-points))
decorated_rankings <- inner_join(athlete_medals_all_years,
athletes_gender,
by = "Name") %>%
arrange(rank_decorated)
appearances_years <- olympics_data %>%
distinct(Name, Year) %>%
group_by(Name) %>%
summarise(no_years = n()) %>%
mutate(normal_years = (no_years - min(no_years))/(max(no_years) - min(no_years)))
no_years_10p <- quantile(appearances_years$no_years, probs = 0.1)
appearances_years <- appearances_years %>%
filter(no_years > no_years_10p )
appearances_events <- olympics_data %>%
group_by(Name) %>%
summarise(no_events = n()) %>%
mutate(normal_events = (no_events - min(no_events))/(max(no_events) - min(no_events)))
no_events_10p <- quantile(appearances_events$no_events, probs = 0.1)
appearances_events <- appearances_events %>%
filter(no_events > no_events_10p )
athlete_medals_events_all_years <- inner_join(athlete_medals_all_years,
appearances_events,
by = "Name")
athlete_medals_events_years <- inner_join(athlete_medals_events_all_years,
appearances_years,
by = "Name") %>%
mutate(impact_points = (points * normal_events)/normal_years,
rank_impact = min_rank(-impact_points)) %>%
select(-rank_decorated, -normal_events, -normal_years)
impact_rankings <- inner_join(athlete_medals_events_years,
athletes_gender,
by = "Name") %>%
arrange(rank_impact)
decorated_rankingsFrom the above rankings, we can conclude that Michael Fred Phelps, II is the most decorated and impactful player ever in the history of the Olympics. He is also the the most decorated and impactful athlete in men. He won a total of 23 gold, 3 silver and 2 bronze medals in 5 appearances across 30 events. Whereas, Larysa Semenivna Latynina (Diriy-) is the most decorated and impactful women athlete. She won 9 gold, 5 Silver and 4 bronze medals in 3 appearances across 19 events.
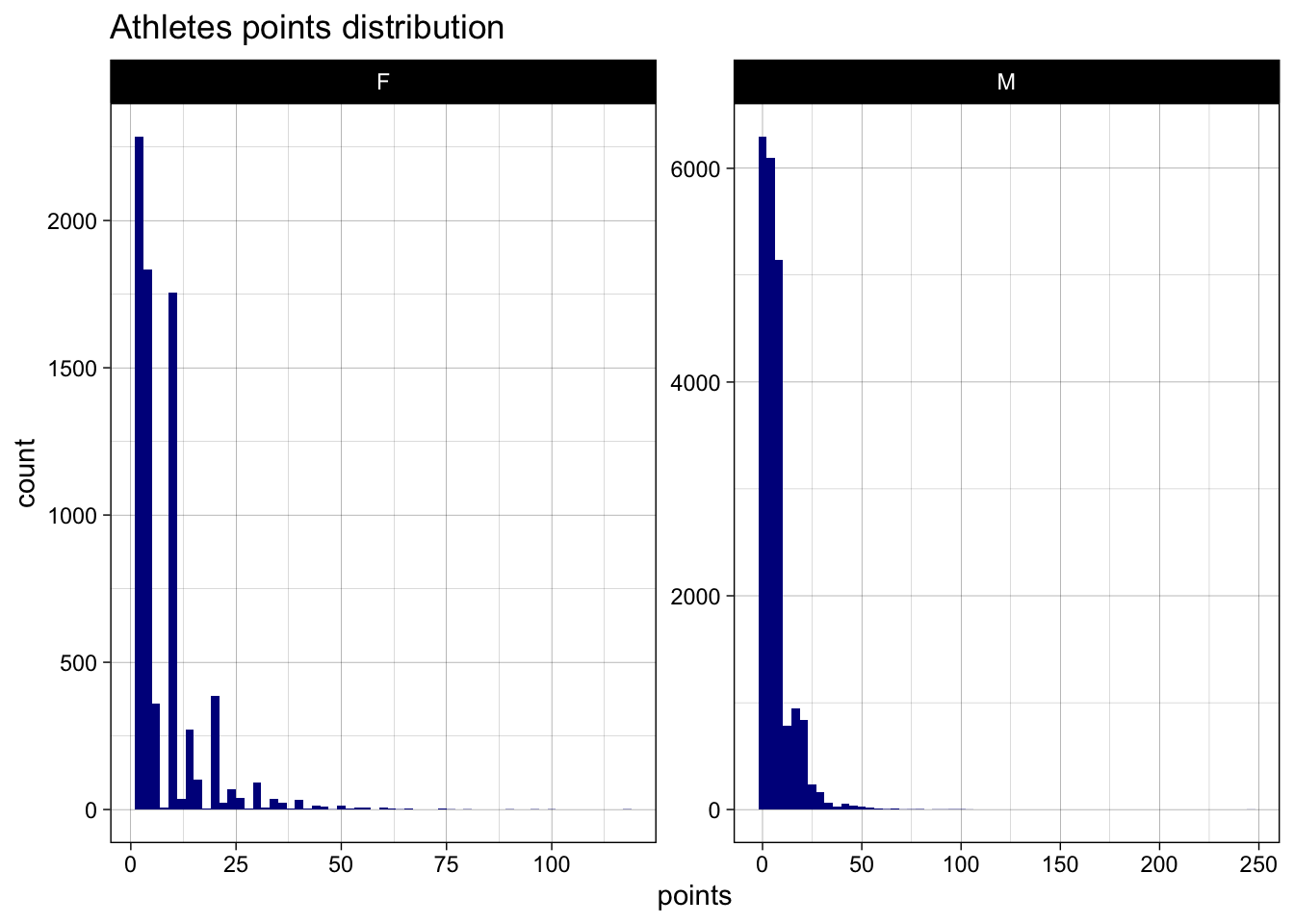
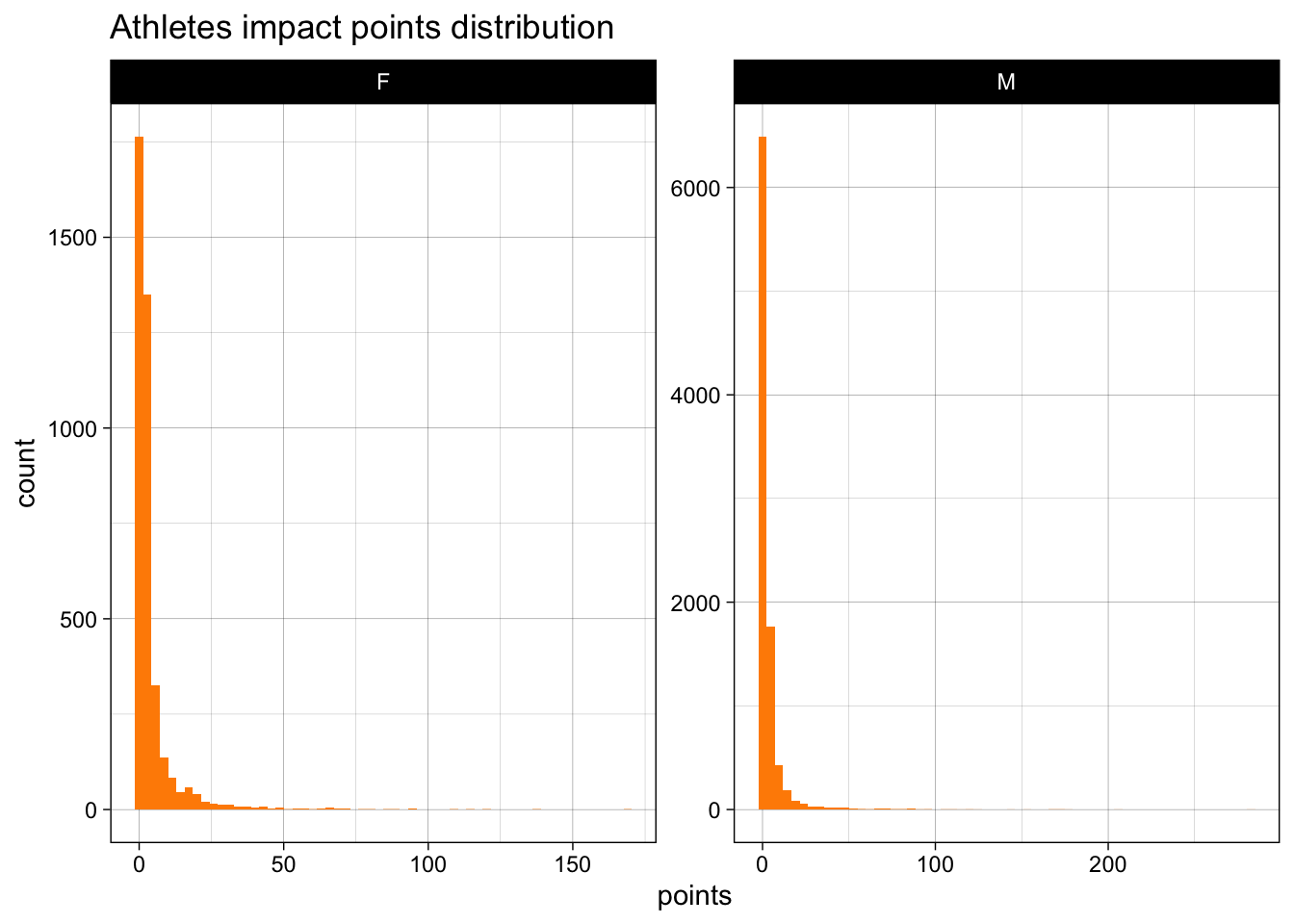
Can we identify the age of men and women athletes where their performance is maximized?
age_wise_medals <- olympics_data %>%
mutate(is_medal_won = case_when(
Medal == "Gold" | Medal == "Silver" | Medal == "Bronze" ~ "medal",
TRUE ~ "no_medal")
) %>%
filter(!is.na(Age)) %>%
group_by(Sex, Age, is_medal_won) %>%
summarise(no_medals = n())
ggplot(age_wise_medals, aes(x=Age, y=no_medals, size = no_medals,color=is_medal_won)) +
geom_point(alpha=0.6) +
scale_size(range = c(.1, 10), name="Medals")+
theme_linedraw()+
facet_wrap(~Sex, scales = "free_x") +
labs(title = "Scatter plot for medals won vs age",
subtitle = "Size of bubble represents number of medals won",
x = "age",
y = "Number of Medals",
color = "Position")+
theme(legend.position = "top")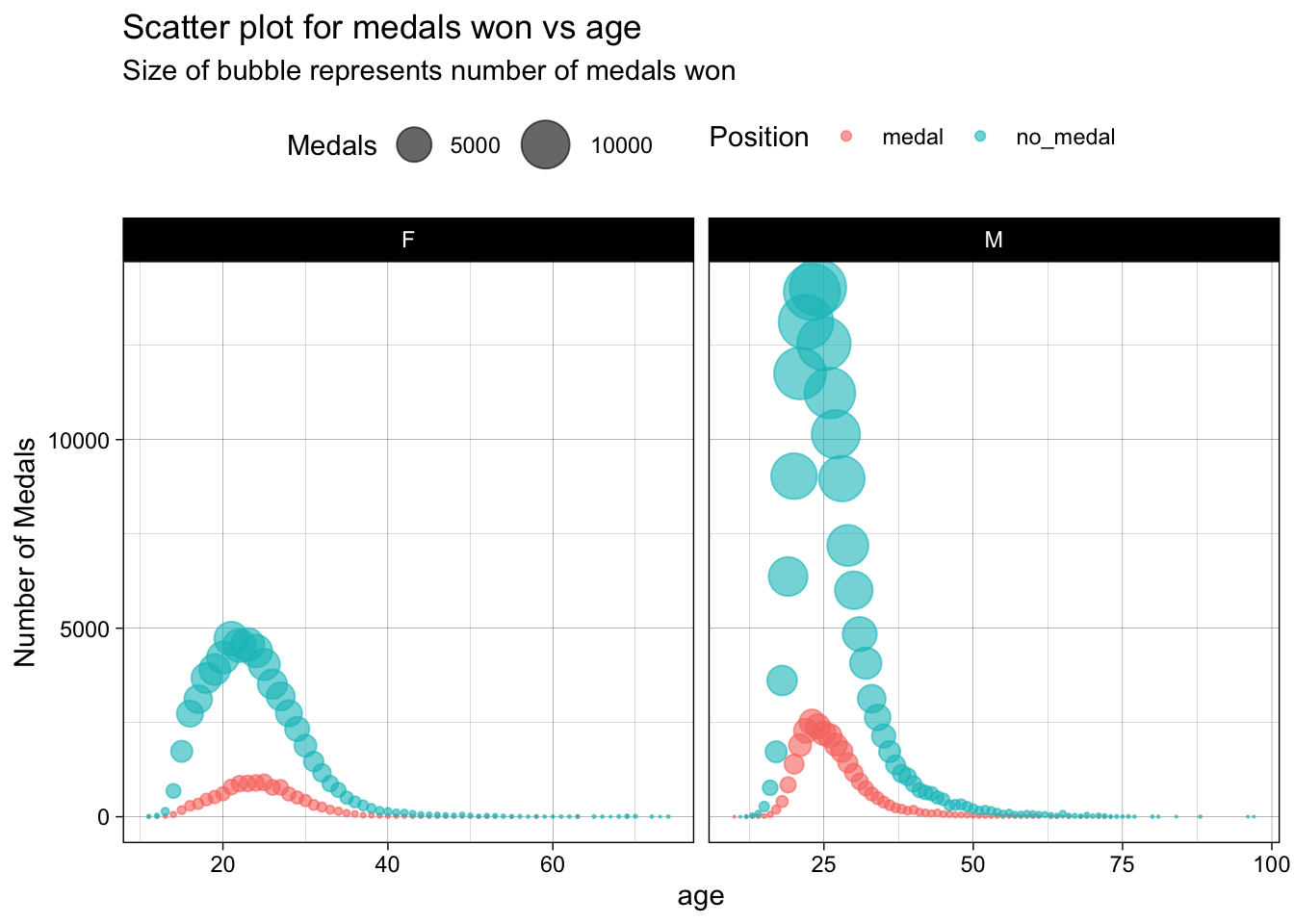
From the above visualizations, we can conclude that peak performance age for male athletes is between 22 to 24 . While for females, it is between 23 to 25. This data is also shown in the tables following the plots.
---
title: "Homework 3"
author: "Srujan Kagitala"
description: ""
date: "7/4/2023"
format:
html:
toc: true
code-fold: true
code-copy: true
code-tools: true
df-print: paged
categories:
- hw3
- olympics
- srujan_kagitala
---
```{r}
#| label: setup
#| warning: false
#| message: false
library(tidyverse)
library(ggplot2)
library(treemap)
knitr::opts_chunk$set(echo = TRUE, warning=FALSE, message=FALSE)
```
## Overview
For my final project, I would do exploratory analysis on the Olympics data right from the year it started in 1896 in Athena till 2016 in Rio de Janeiro.
## Olympics
Olympics is the most decorated sporting event in an athlete's career. The Olympics are the leading international sporting events featuring summer and winter sports competitions in which thousands of athletes from around the world participate in a variety of competitions. The Olympic Games are considered the world's foremost sports competition with more than 200 teams, representing sovereign states and territories, participating. The Olympic Games are normally held every four years, and since 1994, have alternated between the Summer and Winter Olympics every two years during the four-year period. The first, second, and third place finishers in each event receive Olympic medals: gold, silver, and bronze, respectively.
## Dataset
The dataset I would use for this analysis is downloaded from
[Kaggle](https://www.kaggle.com/datasets/samruddhim/olympics-althlete-events-analysis).
This dataset consists of Olympics data of over a century, from the year 1896 to 2016. Studying this dataset will help to understand the patterns followed in the games of Olympics, patterns of the most successful athletes and countries in their Olympics journey and much more!
```{r}
#| label: read
olympics_data <- read_csv("_data/athlete_events_olympics.csv")
olympics_data
```
The data set has `r nrow(olympics_data)` observations and `r ncol(olympics_data)` data points recorded per observation. Each observation records variables like `r names(olympics_data)`.
The youngest and the oldest athlete that ever participated are `r min(olympics_data$Age, na.rm = TRUE)` and `r max(olympics_data$Age, na.rm = TRUE)` years of age respectively. Athletes from across the world compete in `r length(unique(olympics_data$Event))` events that happen across `r length(unique(olympics_data$Sport))` sports. These happen in `r length(unique(olympics_data$Season))` Olympic seasons i.e `r unique(olympics_data$Season)`.
## Data Cleaning
The dataset is mostly clean and we don't have to work around much. Although, for doing some analysis, we might need to create various subsets of data like medals, teams, etc, drop na values for a few variables and mutate new variables(Most of these can be done during the analysis). We need to convert categorical variables into factor to get overall summary across various variables. We don't need the "ID" column for our analysis as it only serves the purpose of a key.
```{r}
#| label: clean
olympics_data <- olympics_data %>%
mutate_if(is_character, as.factor) %>%
select(-ID)
medals <- olympics_data %>%
filter(!is.na(Medal))
summary(olympics_data)
olympics_data
medals
```
## Insights
```{r}
#| label: insight_1
#Type of medals won by teams.
teams_medals_type <- medals %>%
group_by(NOC, Medal) %>%
summarise(count = n())
#Total medals won by teams
teams_medals_total <- medals %>%
group_by(NOC) %>%
summarise(total_medals = n()) %>%
arrange(desc(total_medals))
#Top 50 countries(by total medals won) medal_type tally.
(teams_medals_tally <- inner_join(teams_medals_type,
teams_medals_total[1:50, ],
by = "NOC") %>%
arrange(desc(total_medals)))
#Bar plot of medals won by top 50 countries.
ggplot(data = teams_medals_tally , aes(x= reorder(NOC, total_medals), y = count)) +
geom_bar(stat = "identity",
mapping = aes(fill = Medal),
position = "stack") +
labs(title ="Top 50 countries that won most medals",
y = "No of medals",
x = "Nation of Origin",
fill = "Medal")+
coord_flip()
```
We can see that USA has won the highest number of medals, more than double the number of medals won by Soviet Union.
```{r}
#| label: insight_2
#Sport with events count
(sport_events <- olympics_data %>%
distinct(Sport, Event) %>%
group_by(Sport) %>%
summarise(no_events = n()) %>%
arrange(desc(no_events)))
#Treemap representing each Sport proportional to number of events in olympics
treemap(sport_events,
index = "Sport",
vSize = "no_events",
type = "index",
fontsize.labels = 10,
fontcolor.labels = "black",
align.labels=list(
c("center", "center")),
inflate.labels=F,
palette = "Set1",
title="Treemap representing each Sport proportional to number of events in olympics",
fontsize.title=12)
```
Athletics and shooting are the sports with highest number of events (`r sport_events$no_events[1]` events each) followed by swimming with `r sport_events$no_events[3]` events.
```{r}
#| label: insight_3
#Age distribution among females and males in olympics.
ggplot(olympics_data, aes(x = Age, na.rm = TRUE)) +
geom_histogram(bins = 85, fill="darkred", alpha=0.7) +
theme_linedraw() +
facet_wrap(~Sex, scales = "free") +
labs(title = "Age distribution of atheletes in Olympics",
x = "Age",
y = "Counts")
```
We can see that the mean age of men athletes is higher than the mean age of women athletes.
Most frequent age in men athletes is approximately equal to the most frequent age in women athletes.
```{r}
#| label: insight_4
#Times series for how top 10 nations performed over years.
teams_medals_yearly <- medals %>%
filter(NOC %in% teams_medals_total[1:9,]$NOC) %>%
group_by(NOC, Year) %>%
summarise(total_medals = n()) %>%
arrange(NOC,Year)
ggplot(teams_medals_yearly,
aes(x= Year, y = total_medals)) +
geom_line(color = "darkgreen") +
facet_wrap(~NOC, scales = "free") +
#scale_x_continuous(breaks = c(2015, 2016, 2017),
#labels = c("2015", "2016", "2017")) +
theme_linedraw()+
labs(title = "Medals won over years by top 10 countries since 1896",
x = "Year",
y = "Number of medals")
```
## Ranking System
Is there an unbiased ranking system to determine the rankings of nations in Olympics? Can we rank different nations on varied ranking systems (different weightage for gold, silver and bronze) and observe how their ranks differ based on weightage given to gold, silver and bronze medals?
```{r}
#| label: ranking
(countries_participated_year <- olympics_data %>%
distinct(NOC, Year)%>%
group_by(Year) %>%
summarise(no_countries_participated = n()) %>%
arrange(desc(no_countries_participated)))
```
`r length(unique(olympics_data$NOC))` countries participated in Olympics since the start till the event in 2016. So, we will analyse how varied ranking systems for different years(approx two or three years) in which the number of countries participated is greater than 200 to ensure that we find an unbiased ranking system. We will use that system to rank nations for one random year and also over the years.
**Design.**
The total weighted medal values for each country determine the country’s rank in the Olympics. The weighted value of the medals won by a country is found by multiplying the number of gold, silver and bronze medals by their respective weight and then summing them.
Bronze medals are always worth one point. Gold medals can’t be worth less than silver and silver can’t be worth less than bronze.
A ranking system is defined by silver multiplier and gold multiplier (bronze is always worth 1 point).The weighted value for silver in a ranking system is calculated by multiplying the number of silver medals by weight multiplier of silver. The weight for gold in a ranking system is calculated by multiplying the number of gold medals by weight multiplier of gold. Each country’s weighted medal values are summed for each medal. These totals are ranked in such a fashion that the lowest rank is allotted to the country with the highest weighted value.
Description of Ranking Systems used in the analysis. (Each system is defined by silver and gold multiplier)
1. System 1 - Silver multiplier = Gold multiplier = 1. All medals are weighed equally. So, the nations are ranked based on the total medals won.
2. System 2 - Silver multiplier = 2, Gold multiplier = 5.
3. System 3 - Silver multiplier = 5, Gold multiplier = 5.
4. System 4 - Silver multiplier = 2, Gold multiplier = 10.
5. System 5 - Silver multiplier = 5, Gold multiplier = 10.
6. System 6 - Silver multiplier = 5, Gold multiplier = 20.
7. System 7 - Bronze mutliplier = Silver multiplier = 0, Gold multiplier = 1. Only gold medals are important.
I will verify the ranking systems for years 2016 and 2008.
```{r}
#| label: ranking_2016
(medals_2016 <- medals %>%
filter(Year == 2016) %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(system_1 = Gold + Silver + Bronze,
rank_1 = min_rank(-system_1),
system_2 = 5*Gold + 2*Silver + Bronze,
rank_2 = min_rank(-system_2),
system_3 = 5*Gold + 5*Silver + Bronze,
rank_3 = min_rank(-system_3),
system_4 = 10*Gold + 2*Silver + Bronze,
rank_4 = min_rank(-system_4),
system_5 = 10*Gold + 5*Silver + Bronze,
rank_5 = min_rank(-system_5),
system_6 = 20*Gold + 5*Silver + Bronze,
rank_6 = min_rank(-system_6),
system_7 = Gold,
rank_7 = min_rank(-system_7)) %>%
arrange(rank_1))
ranks_2016 <- medals_2016 %>%
select(NOC, rank_1, rank_2, rank_3, rank_4, rank_5, rank_6, rank_7) %>%
arrange(rank_1) %>%
slice(1:50) %>%
pivot_longer(c("rank_1", "rank_2", "rank_3", "rank_4", "rank_5", "rank_6", "rank_7"),
names_to = "type",
values_to = "rank")
ggplot(ranks_2016, aes(x = type, y=NOC, label=rank, fill=rank)) +
geom_tile() +
geom_text(color = "white", size = 2)+
scale_fill_continuous(low = "darkorange",
high = "darkblue",
name = "rank") +
theme(axis.text.x = element_text(angle = 90),
axis.text.y = element_text(size = 6))+
labs(title = "Heatmap of rankings for top 50 total medal winning countries in 2016",
y = "Nation",
x = "Ranking System")
```
From the above heatmap of rankings for year 2016, we can see that, rank_5 has the least deviation from rankings by other systems for most of the countries. Also, rank_2 is fairly close to most of the other rankings. Hence, either of them can be used as the best estimator of country rankings for the year 2016. Likewise, let's verify for year 2008 and see if there is a common best system for both the years.
```{r}
#| label: ranking_2008
(medals_2008 <- medals %>%
filter(Year == 2008) %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(system_1 = Gold + Silver + Bronze,
rank_1 = min_rank(-system_1),
system_2 = 5*Gold + 2*Silver + Bronze,
rank_2 = min_rank(-system_2),
system_3 = 5*Gold + 5*Silver + Bronze,
rank_3 = min_rank(-system_3),
system_4 = 10*Gold + 2*Silver + Bronze,
rank_4 = min_rank(-system_4),
system_5 = 10*Gold + 5*Silver + Bronze,
rank_5 = min_rank(-system_5),
system_6 = 20*Gold + 5*Silver + Bronze,
rank_6 = min_rank(-system_6),
system_7 = Gold,
rank_7 = min_rank(-system_7)) %>%
arrange(rank_1))
ranks_2008 <- medals_2008 %>%
select(NOC, rank_1, rank_2, rank_3, rank_4, rank_5, rank_6, rank_7) %>%
arrange(rank_1) %>%
slice(1:50) %>%
pivot_longer(c("rank_1", "rank_2", "rank_3", "rank_4", "rank_5", "rank_6", "rank_7"),
names_to = "type",
values_to = "rank")
ggplot(ranks_2008, aes(x = type, y=NOC, label=rank, fill=rank)) +
geom_tile() +
geom_text(color = "white", size = 2)+
scale_fill_continuous(low = "darkorange",
high = "darkblue",
name = "rank") +
theme(axis.text.x = element_text(angle = 90),
axis.text.y = element_text(size = 6))+
labs(title = "Heatmap of rankings for top 50 total medal winning countries in 2008",
y = "Nation",
x = "Ranking System")
```
From the above heatmap of rankings for year 2008, we can see that, rank_5 has the least deviation from rankings by other systems for most of the countries. Also, rank_3 is fairly close to most of the other rankings. Hence, either of them can be used as the best estimators of country rankings for the year 2008.
Analysis on 2008 and 2016 showed that ranking system 5 has the least deviation from other rankings. So, we can use this as the best estimator for ranking nations. This might not be completely unbiased but it fairly ranks the countries according to the medals won.
Below table shows rankings of countries for the year 1912 using system 5.
```{r}
#| label: ranking_1912
(medals_1912 <- medals %>%
filter(Year == 1912) %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(points = 10*Gold + 5*Silver + Bronze,
rank = min_rank(-points)) %>%
arrange(rank))
```
Let's see the overall rankings from 1896 to 2016 using ranking system 5. We will rank based on average_points per appearance. Total points is divided by number of appearances to eliminate bias (to some extent) that occurs from the fact that a few nations might take part more number of times compared to others. Only nations above 10th percentile of number of appearances are ranked because there could be outliers on the lower end (especially countries who participated only once).
```{r}
#| label: ranking_overall
medals_all_years <- medals %>%
group_by(NOC, Medal) %>%
summarise(count = n()) %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(points = 10*Gold + 5*Silver + Bronze)
appearances <- olympics_data %>%
distinct(NOC, Year) %>%
group_by(NOC) %>%
summarise(no_appearances = n())
no_appearances_10p <- quantile(appearances$no_appearances, probs = 0.1)
appearances <- appearances %>%
filter(no_appearances > no_appearances_10p )
medals_all_years <- inner_join(medals_all_years,
appearances,
by = "NOC") %>%
mutate(avg_points_per_appearance = points/no_appearances,
rank = min_rank(-avg_points_per_appearance)) %>%
arrange(rank)
medals_all_years
```
## Decorated Athletes
Can we identify the most decorated athlete of all time, most decorated men and women athlete?
First we compute the weighted value of medals (points) won by athletes across years using ranking system 5 (the best ranking system as shown previously). The most decorated athlete is definitely based on the number of points earned.
Another ranking system can be designed based on overall number of events the athlete has participated in years and the number of appearances over years. This can be defined as impact rankings. This system tries to give more weightage to points scored by athletes who scored comparable points in lesser time frames(either lesser appearances or lesser events). Impact ranking is based on extrapolated impact points. Impact points are calculated by using points, normalized number of events (normal_events) and normalized number of appearances(normal_years). Only athletes with number of events and number of appearances above 10th percentile are ranked because there could be outliers on the lower end (especially for those who either participated in a single event or only appeared once).
$$ impact\_points = (points * normal\_events)/normal\_years $$
```{r}
#| label: question1
athletes_gender <- olympics_data %>%
distinct(Name, Sex) %>%
select(Name, Sex)
athlete_medals_all_years <- medals %>%
group_by(Name, Medal) %>%
summarise(count = n()) %>%
ungroup() %>%
pivot_wider(names_from=Medal, values_from=count, values_fill=0) %>%
ungroup %>%
mutate(points = 10*Gold + 5*Silver + Bronze,
rank_decorated = min_rank(-points))
decorated_rankings <- inner_join(athlete_medals_all_years,
athletes_gender,
by = "Name") %>%
arrange(rank_decorated)
appearances_years <- olympics_data %>%
distinct(Name, Year) %>%
group_by(Name) %>%
summarise(no_years = n()) %>%
mutate(normal_years = (no_years - min(no_years))/(max(no_years) - min(no_years)))
no_years_10p <- quantile(appearances_years$no_years, probs = 0.1)
appearances_years <- appearances_years %>%
filter(no_years > no_years_10p )
appearances_events <- olympics_data %>%
group_by(Name) %>%
summarise(no_events = n()) %>%
mutate(normal_events = (no_events - min(no_events))/(max(no_events) - min(no_events)))
no_events_10p <- quantile(appearances_events$no_events, probs = 0.1)
appearances_events <- appearances_events %>%
filter(no_events > no_events_10p )
athlete_medals_events_all_years <- inner_join(athlete_medals_all_years,
appearances_events,
by = "Name")
athlete_medals_events_years <- inner_join(athlete_medals_events_all_years,
appearances_years,
by = "Name") %>%
mutate(impact_points = (points * normal_events)/normal_years,
rank_impact = min_rank(-impact_points)) %>%
select(-rank_decorated, -normal_events, -normal_years)
impact_rankings <- inner_join(athlete_medals_events_years,
athletes_gender,
by = "Name") %>%
arrange(rank_impact)
decorated_rankings
impact_rankings
```
From the above rankings, we can conclude that Michael Fred Phelps, II is the most decorated and impactful player ever in the history of the Olympics. He is also the the most decorated and impactful athlete in men. He won a total of 23 gold, 3 silver and 2 bronze medals in 5 appearances across 30 events. Whereas, Larysa Semenivna Latynina (Diriy-) is the most decorated and impactful women athlete. She won 9 gold, 5 Silver and 4 bronze medals in 3 appearances across 19 events.
```{r}
#| label: question1_plot
ggplot(decorated_rankings, aes(points)) +
geom_histogram( bins = 60, fill="darkblue") +
theme_linedraw() +
facet_wrap(~Sex, scales = "free") +
labs(title = "Athletes points distribution")
ggplot(impact_rankings, aes(impact_points)) +
geom_histogram(bins = 60, fill="darkorange") +
theme_linedraw() +
facet_wrap(~Sex, scales = "free") +
labs(title = "Athletes impact points distribution",
x = "points")
```
## Peak Performant Age
Can we identify the age of men and women athletes where their performance is maximized?
```{r}
#| label: performance
age_wise_medals <- olympics_data %>%
mutate(is_medal_won = case_when(
Medal == "Gold" | Medal == "Silver" | Medal == "Bronze" ~ "medal",
TRUE ~ "no_medal")
) %>%
filter(!is.na(Age)) %>%
group_by(Sex, Age, is_medal_won) %>%
summarise(no_medals = n())
ggplot(age_wise_medals, aes(x=Age, y=no_medals, size = no_medals,color=is_medal_won)) +
geom_point(alpha=0.6) +
scale_size(range = c(.1, 10), name="Medals")+
theme_linedraw()+
facet_wrap(~Sex, scales = "free_x") +
labs(title = "Scatter plot for medals won vs age",
subtitle = "Size of bubble represents number of medals won",
x = "age",
y = "Number of Medals",
color = "Position")+
theme(legend.position = "top")
(age_wise_medals %>%
filter(Sex == "M",
is_medal_won == "medal") %>%
arrange(desc(no_medals)) %>%
select(-is_medal_won))
(age_wise_medals %>%
filter(Sex == "F",
is_medal_won == "medal") %>%
arrange(desc(no_medals)) %>%
select(-is_medal_won))
```
From the above visualizations, we can conclude that peak performance age for male athletes is between 22 to 24 . While for females, it is between 23 to 25. This data is also shown in the tables following the plots.
## Limitations
1. It is quite tough to identify decorated/impactful athletes just from visualizations.
2. Identifying the best ranking systems from heatmap could be challenging for general audience. But can be done.
3. Need to check if peak performance age varies across countries.
4. Research question to be figured out - "Can we identify if there is a correlation of features like height/weight/age to a specific sports? (For example if height positively impacts basketball, age helps in shooting or athletics, etc.) Does it equally hold for both the genders?"
3. Need to add references section.
4. Will add more plots to show variation in peak performance age across countries. Also more visualizations around how traits are important for a sport if there is a correlation.