Week 2/3/4 Challenge Solutions

challenge_2

challenge_3

challenge_4

solution

Analyzing the Complex Structure of the Economic Input-Output Network of the US, 2012

Author

Oriol Vallès Codina

US Bureau of Economic Analysis - Input-Output Network

Package Load

Before starting, the necessary packages should be loaded. For this analysis, we are going to use igraph, but other options can be contemplated depending on your needs.

library(readxl)
library(tidyverse)
library(igraph)
library(reshape2)

knitr::opts_chunk$set(echo = TRUE, warning = FALSE, message=FALSE)

Data Preparation

Motivated by the recent shocks on global supply chains, we are interested in analyzing and visualizing the complex structure of the inter-industry economic transactions of the United States. In economic analysis, this information is contained in the so-called input-output table, which many national and international databases document at different levels of industry aggregation (26, 50, 405, 800+…). From a network perspective, an input-output table is an asymmetric, weighted adjacency matrix where the weights correspond to the input value required to produce a unit of output, that is, its direct requirements.

Data is directly loaded reading a xlsx file using the readxl package. Note that the file features two years, 2007 and 2012.

filename <- '../posts/_data/US_input_output_table_2007_and_2012.xlsx' # while on console
filename <- '_data/US_input_output_table_2007_and_2012.xlsx' # while rendering
data <- read_xlsx(filename, sheet = "2012")

First of all, we explore the data: its dimensions and the values at its corners so we can extract the adjacency matrix.

dim(data)

[1] 413 407

data[1 : 10, 1 : 10]

commodities <- unlist(data[5 : 409, 2])
industries <- unlist(data[3, 3 : 407])

In this particular case, each column of the table displays the values of 405 commodities required by a specific industry. The input-output table is commodity-by-industry with commodities in the rows and industries in the columns, in a way that the list of commodities and industries do not necessarily match so we need to harmonize them to construct the adjacency matrix.

table(commodities %in% industries)


FALSE  TRUE 
    4   401

table(industries %in% commodities)


FALSE  TRUE 
    4   401

io.table <- data[5 : 409, 3 : 407] %>% as.matrix
io.table <- apply(io.table, 1, as.numeric) %>% t

colnames(io.table) <- industries
rownames(io.table) <- commodities

sectors <- industries[industries %in% commodities]
io.table <- io.table[sectors, sectors]

go <- rowSums(io.table)

Graph Analysis

Once the adjacency matrix is constructed, we can now analyze and visualize the graph:

g <- graph_from_adjacency_matrix(io.table, mode = 'directed', weighted = TRUE, add.rownames = TRUE)

Size

The network has the same amount of vertices than the number of rows and columns of the adjacency matrix:

vcount(g)

[1] 401

and the following number of edges,

ecount(g)

[1] 51860

The network is relatively sparse:

table(io.table > 0) / length(sectors) ^ 2


    FALSE      TRUE 
0.6775393 0.3224607

io.table[io.table < 0] <- 0

prob <- (table(io.table > 0) / length(sectors) ^ 2)['TRUE']

Degree

It is useful to compute the different degree concepts of the network and observe its distributions:

nodes <- data.frame(name = V(g)$name,
                    output = rowSums(io.table),
                    all.degree = degree(g, mode = 'all'), 
                    out.degree = degree(g, mode = 'out'),
                    in.degree = degree(g, mode = 'in'), 
                    total.degree = degree(g, mode = 'total'),
                    eigen.centrality = evcent(g)$vector)

head(nodes)

nodes %>% melt %>% filter(variable != 'output' & variable != 'eigen.centrality') %>% 
  ggplot(aes(x = value, fill = variable, color = variable)) + geom_density(alpha = .2, bw = 5) +
  ggtitle('Degree Distribution')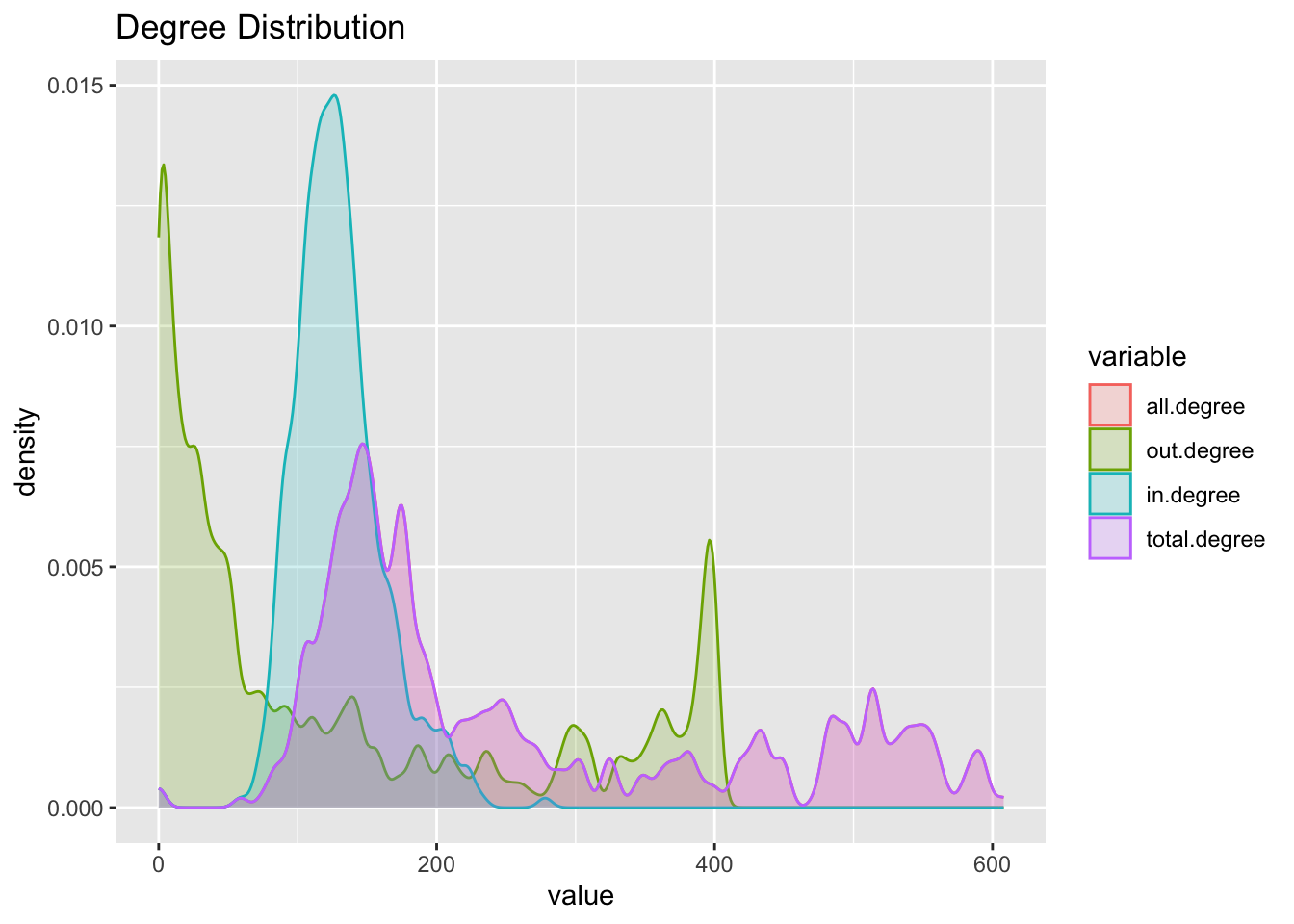

corrplot :: corrplot(cor(nodes[ , -1]), title = 'Correlation Plot')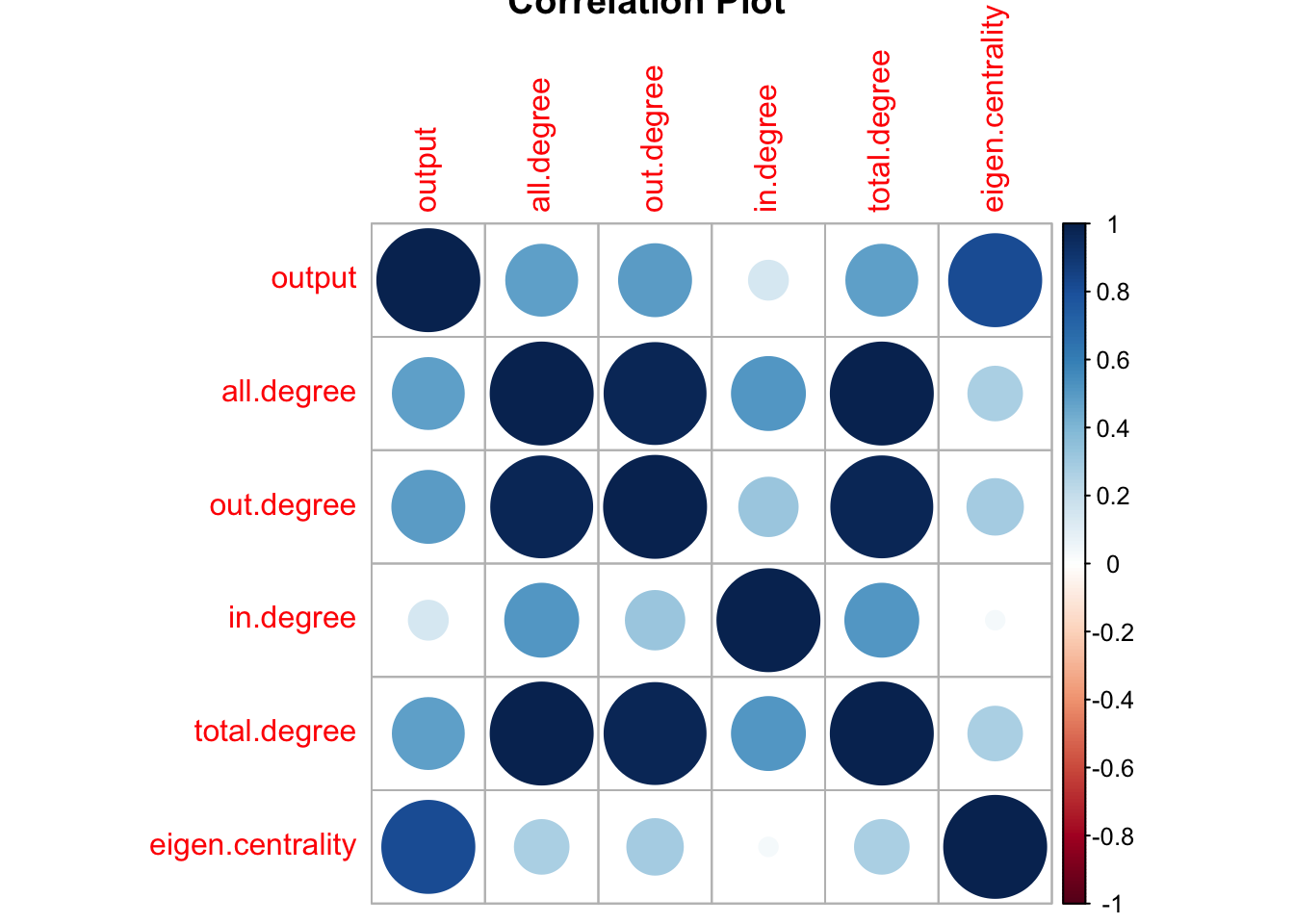

kableExtra :: kable(apply(nodes[ , -1], 2, function (x) nodes$name[order(x, decreasing = TRUE)][1 : 10]))

output	all.degree	out.degree	in.degree	total.degree	eigen.centrality
Management of companies and enterprises	Nonresidential maintenance and repair	Electric power generation, transmission, and distribution	Scientific research and development services	Nonresidential maintenance and repair	Iron and steel mills and ferroalloy manufacturing
Iron and steel mills and ferroalloy manufacturing	Full-service restaurants	Water, sewage and other systems	Hospitals	Full-service restaurants	Management of companies and enterprises
Other real estate	Wired telecommunications carriers	Professional and commercial equipment and supplies	State and local government other services	Wired telecommunications carriers	Plastics material and resin manufacturing
Other durable goods merchant wholesalers	Limited-service restaurants	Machinery, equipment, and supplies	Other amusement and recreation industries	Limited-service restaurants	Petroleum refineries
Petroleum refineries	Services to buildings and dwellings	Other durable goods merchant wholesalers	Management of companies and enterprises	Services to buildings and dwellings	Other durable goods merchant wholesalers
Electric power generation, transmission, and distribution	Architectural, engineering, and related services	Grocery and related product wholesalers	Junior colleges, colleges, universities, and professional schools	Architectural, engineering, and related services	Other real estate
Truck transportation	Wireless telecommunications carriers (except satellite)	Petroleum and petroleum products	Nonresidential maintenance and repair	Wireless telecommunications carriers (except satellite)	Other basic organic chemical manufacturing
Other nondurable goods merchant wholesalers	Management of companies and enterprises	Other nondurable goods merchant wholesalers	Accommodation	Management of companies and enterprises	Petrochemical manufacturing
Plastics material and resin manufacturing	Waste management and remediation services	Wholesale electronic markets and agents and brokers	Civic, social, professional, and similar organizations	Waste management and remediation services	Electric power generation, transmission, and distribution
Advertising, public relations, and related services	Other durable goods merchant wholesalers	Air transportation	Architectural, engineering, and related services	Other durable goods merchant wholesalers	Custom roll forming

# top.nodes <- nodes[order(nodes$degree, decreasing = T), ]
# top.nodes[1 : 10, ] %>% ggplot(aes(x = out.degree, y = reorder(name, degree))) + geom_bar(stat = 'identity')

plot(nodes$output, nodes$eigen.centrality)

Dyad Census

A dyad census confirms the input-output network is quite sparse. We could compare this dyad census with the null version of a random network with a similar number of edges:

dyad.census(g)

$mut
[1] 10041

$asym
[1] 31430

$null
[1] 38729

g.random <- erdos.renyi.game(length(sectors), prob, directed = TRUE)

ecount(g.random)

[1] 51650

rbind(IO = dyad.census(g), random = dyad.census(g.random))

       mut   asym  null 
IO     10041 31430 38729
random 8286  35078 36836

Mutual and null dyads are higher for the IO network, while asymmetric dyads are more common for the random network. How do we interpret these results?

Triad Census

triad.labels <- c("A,B,C, the empty graph.",
                  "A->B, C, the graph with a single directed edge.",
                  "A<->B, C, the graph with a mutual connection between two vertices.",
                  "A<-B->C, the out-star.",
                  "A->B<-C, the in-star.",
                  "A->B->C, directed line.","A<->B<-C.",
                  "A<->B->C.",
                  "A->B<-C, A->C.",
                  "A<-B<-C, A->C.",
                  "A<->B<->C.",
                  "A<-B->C, A<->C.",
                  "A->B<-C, A<->C.",
                  "A->B->C, A<->C.",
                  "A->B<->C, A<->C.",
                  "A<->B<->C, A<->C, the complete graph.")

triad.census.data <- data.frame(label = triad.labels, IO = triad.census(g), random = triad.census(g.random)) %>% melt
colnames(triad.census.data) <- c('triad', 'network', 'value')
triad.census.data %>% ggplot(aes(x = value, y = triad, fill = network)) + geom_bar(stat = 'identity', position = 'dodge')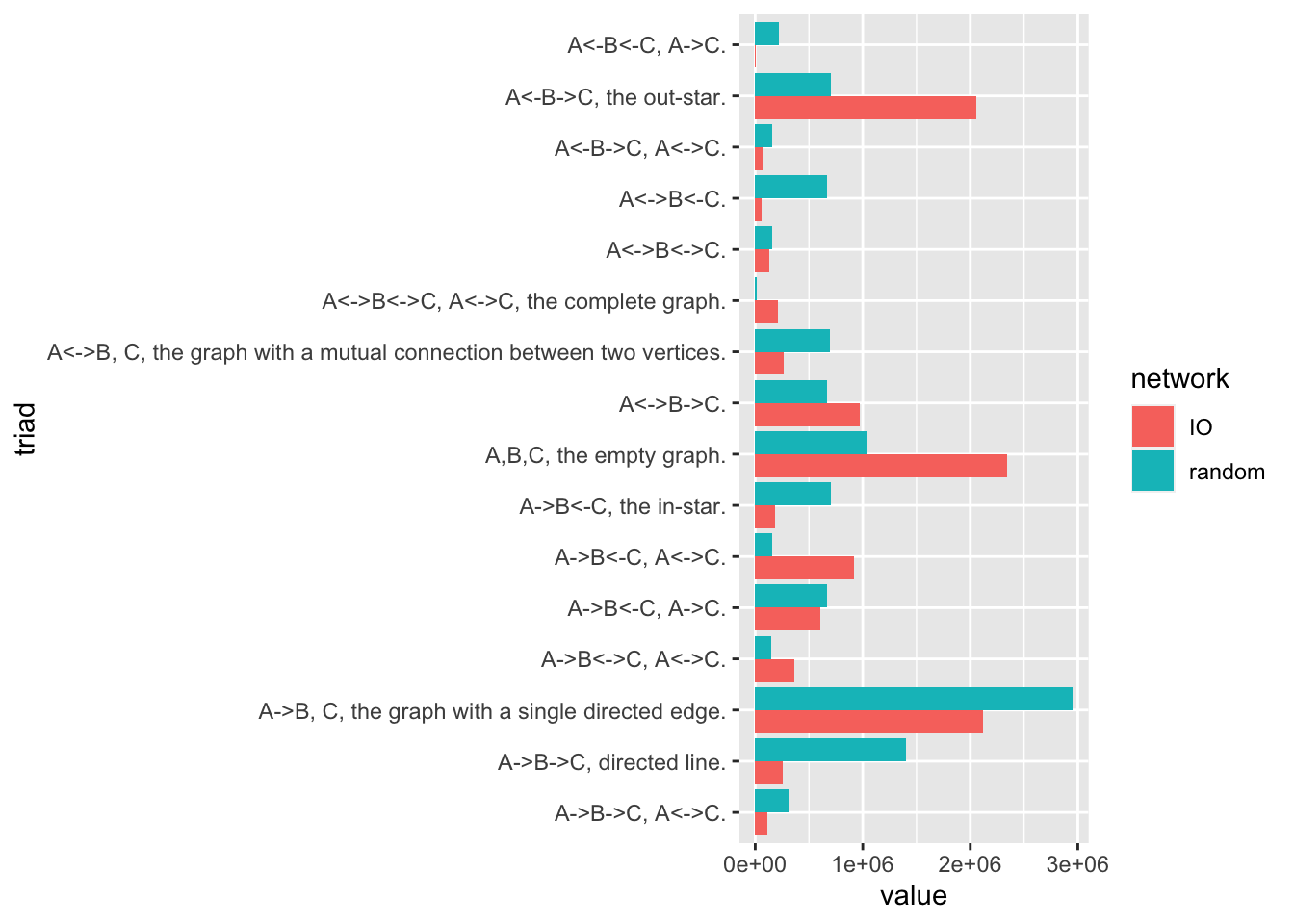

Striking features of the above plot is the over-representation of out-stars, complete, and empty graphs in the input-output case relative to the random graph, while there is an under-representation of graphs with single directed edges and directed lines.

Transitivity

transitivity(g, type = 'global')

[1] 0.6517081

transitivity(g.random, type = 'global')

[1] 0.5408801

nodes$transitivity <- transitivity(g, type = 'local')
nodes$weighted.transitivity <-  transitivity(g, type = 'weighted')

melt(nodes) %>% filter(variable == 'transitivity' | variable == 'weighted.transitivity') %>% 
  ggplot(aes(x = value, fill = variable, color = variable)) + geom_density(alpha = 0.2) +
  ggtitle('Transitivity Distribution, Local and Weighted')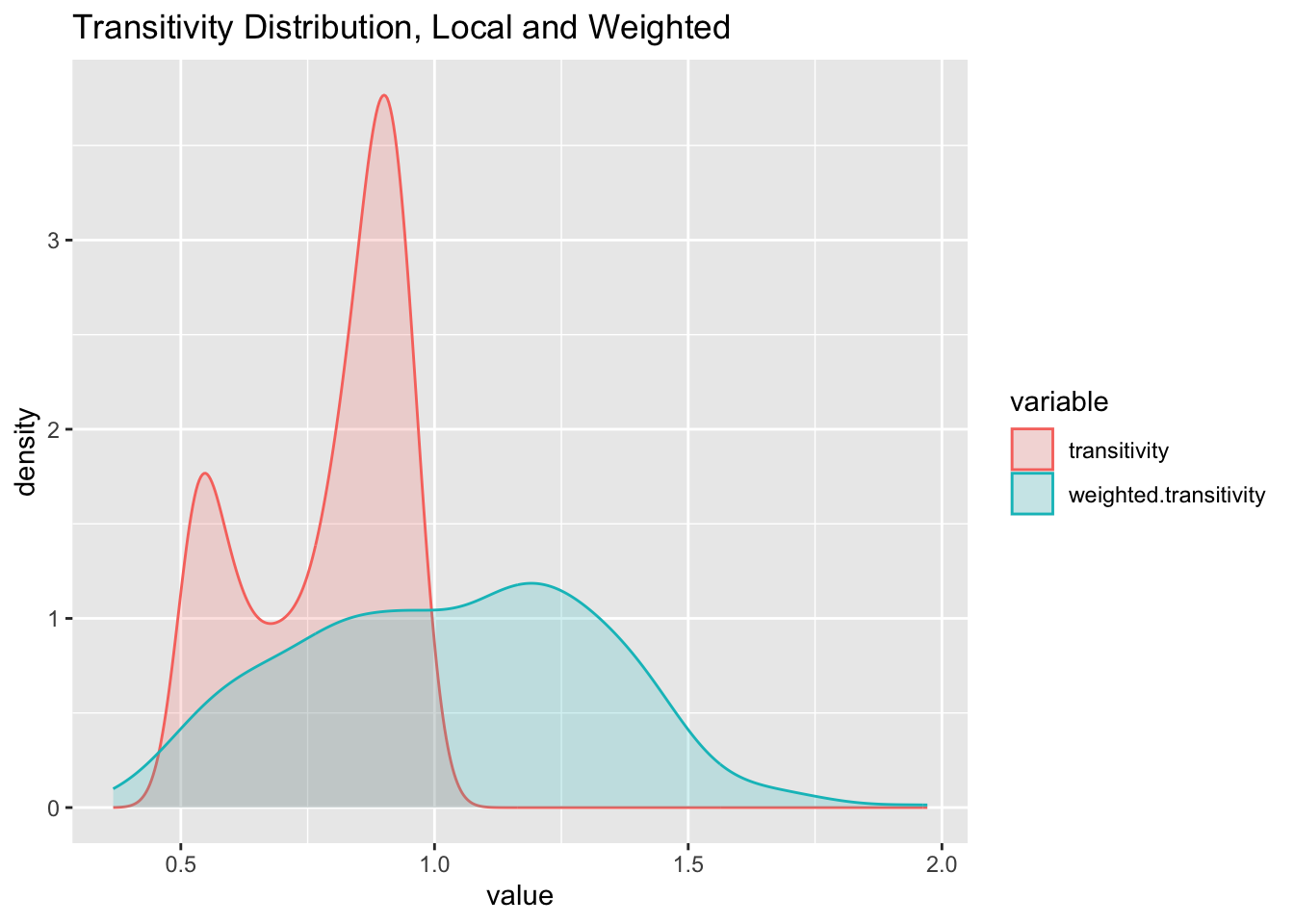

rbind(data.frame(network = 'IO', value = transitivity(g, type = 'local')),
      data.frame(network = 'random', value = transitivity(g.random, type = 'local'))) %>% 
  ggplot(aes(x = value, fill = network, color = network)) + geom_density(alpha = 0.2) +
  ggtitle('Transitivity Distribution by Network')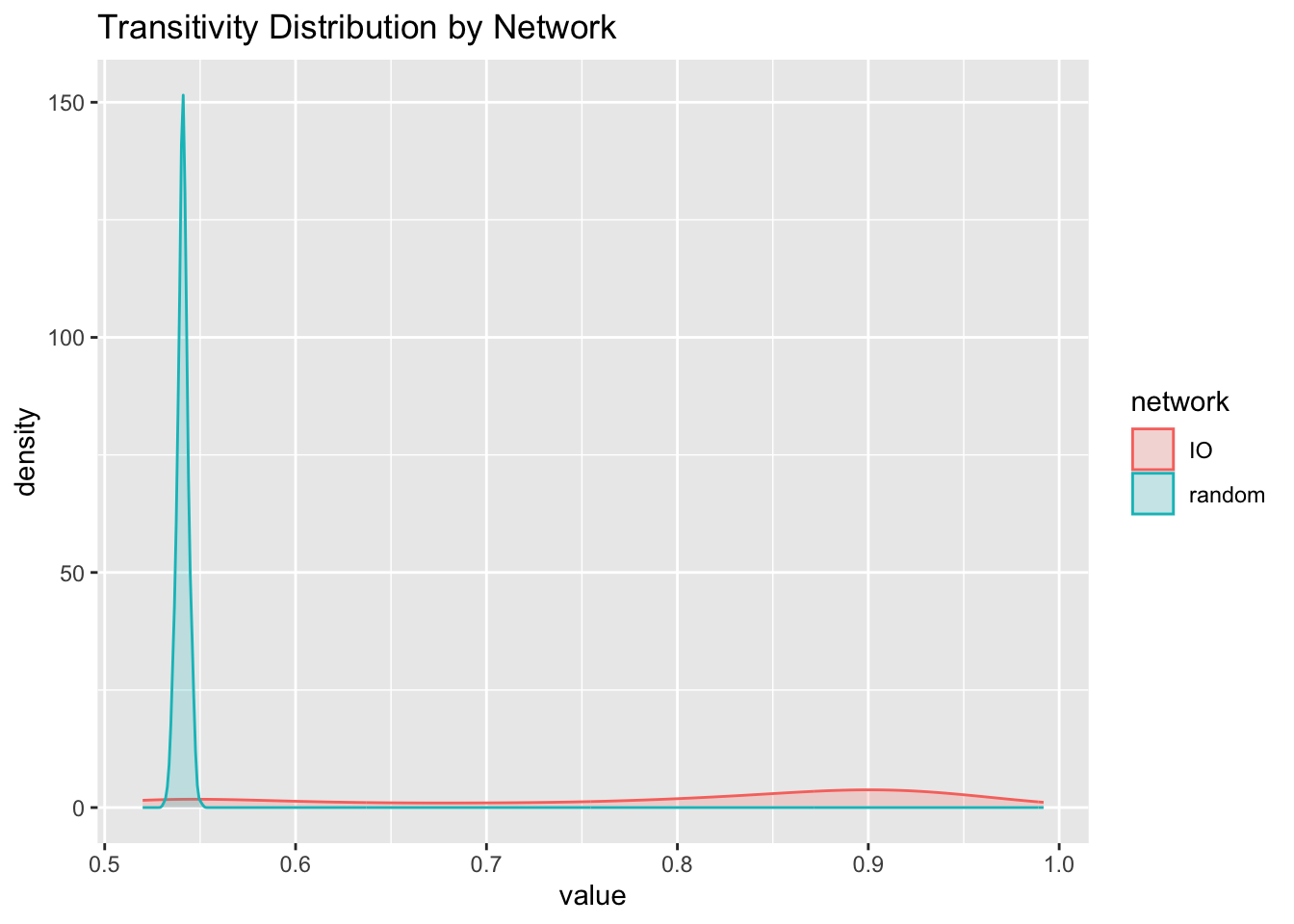

Component Structure

E(g)$weight[E(g)$weight < 0] <- 0

diameter(g)

[1] 0.129843

diameter(g.random)

[1] 2

farthest_vertices(g)

$vertices
+ 2/401 vertices, named, from 3c3e69d:
[1] Dog and cat food manufacturing Printing ink manufacturing    

$distance
[1] 0.129843

wc.g <- cluster_walktrap(g)
member <- membership(wc.g)

nodes$member <- member
table(member)

member
  1   2   3   4   5   6   7   8   9  10  11  12 
  3  38 117 121   8 107   2   1   1   1   1   1

table(member) %>% melt %>% ggplot + geom_bar(aes(x = reorder(member, - value), y = value, fill = factor(member)), stat = 'identity')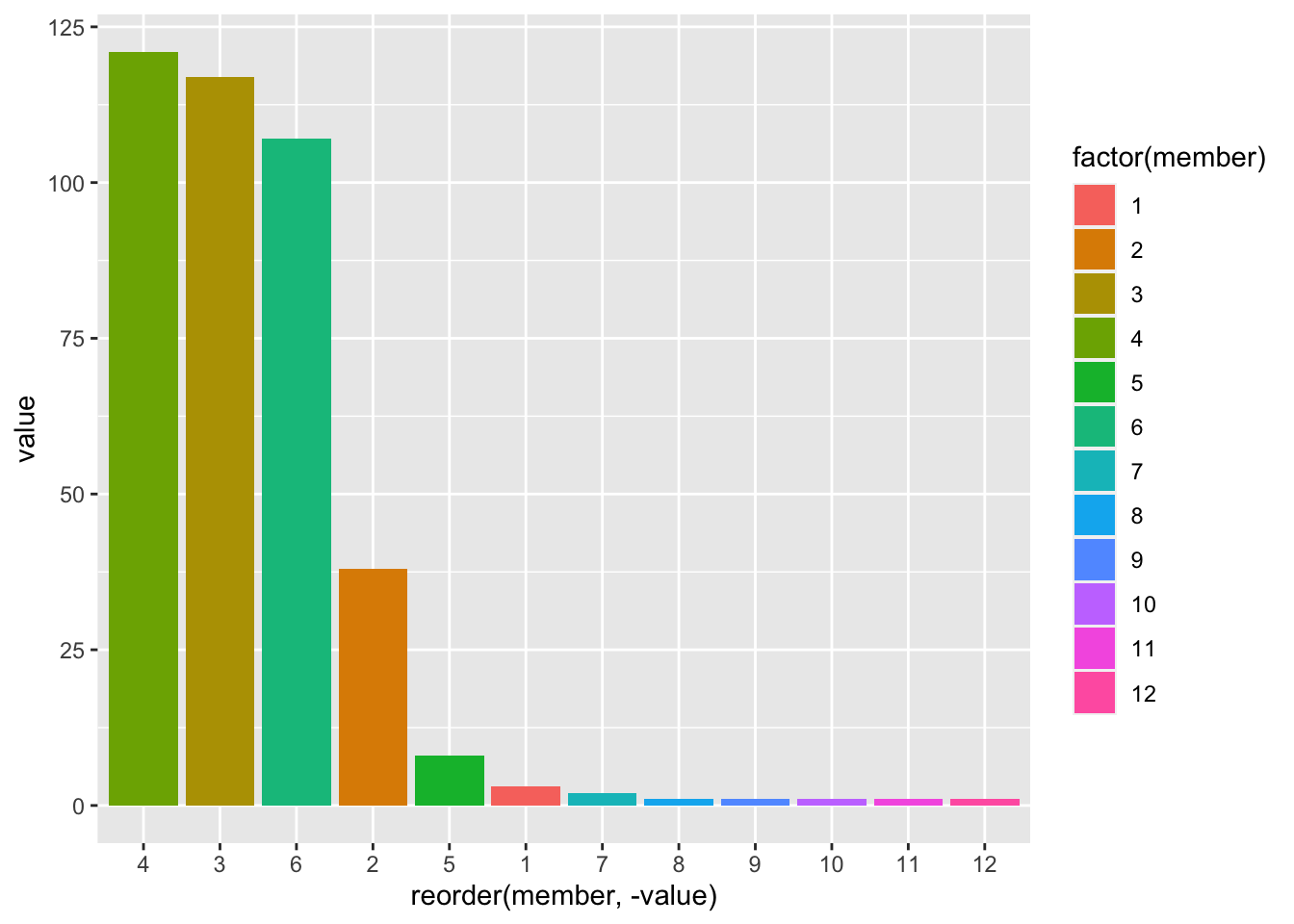

# Percentages of Output of each Component
go.wc.percent <- 100 * sapply(names(table(member)), function(x) sum(go[member==x]))/sum(go)


x <- 4
ord.x <- order(go[member == x], decreasing = T)[1:15]
V(g)$name[member == x][ord.x]

 [1] "Iron and steel mills and ferroalloy manufacturing"       
 [2] "Other durable goods merchant wholesalers"                
 [3] "Nonferrous Metal (except Aluminum) Smelting and Refining"
 [4] "Machinery, equipment, and supplies"                      
 [5] "Semiconductor and related device manufacturing"          
 [6] "Household appliances and electrical and electronic goods"
 [7] "Machine shops"                                           
 [8] "Turned product and screw, nut, and bolt manufacturing"   
 [9] "Copper rolling, drawing, extruding and alloying"         
[10] "Other Motor Vehicle Parts Manufacturing"                 
[11] "Aluminum product manufacturing from purchased aluminum"  
[12] "Other electronic component manufacturing"                
[13] "Coating, engraving, heat treating and allied activities" 
[14] "Alumina refining and primary aluminum production"        
[15] "All other forging, stamping, and sintering"

largest <- lapply(1:3,
       function(y) 
        {
         x <- c(3,4,6)[y]
         ord.x <- order(go[member == x], decreasing = T)[1:5]
         data.frame(sector = V(g)$name[member == x][ord.x],
                    output = go[member == x][ord.x],
                    prcnt = round(100 * go[member == x][ord.x]/sum(go),2),
                    component = as.factor(x),
                    row.names = NULL)
       })

bind_rows(largest) %>% ggplot(aes(y=reorder(sector, prcnt), x=prcnt, fill=component, label=round(prcnt,2))) +
  geom_bar(stat="identity") + ylab('') + xlab('% of Output')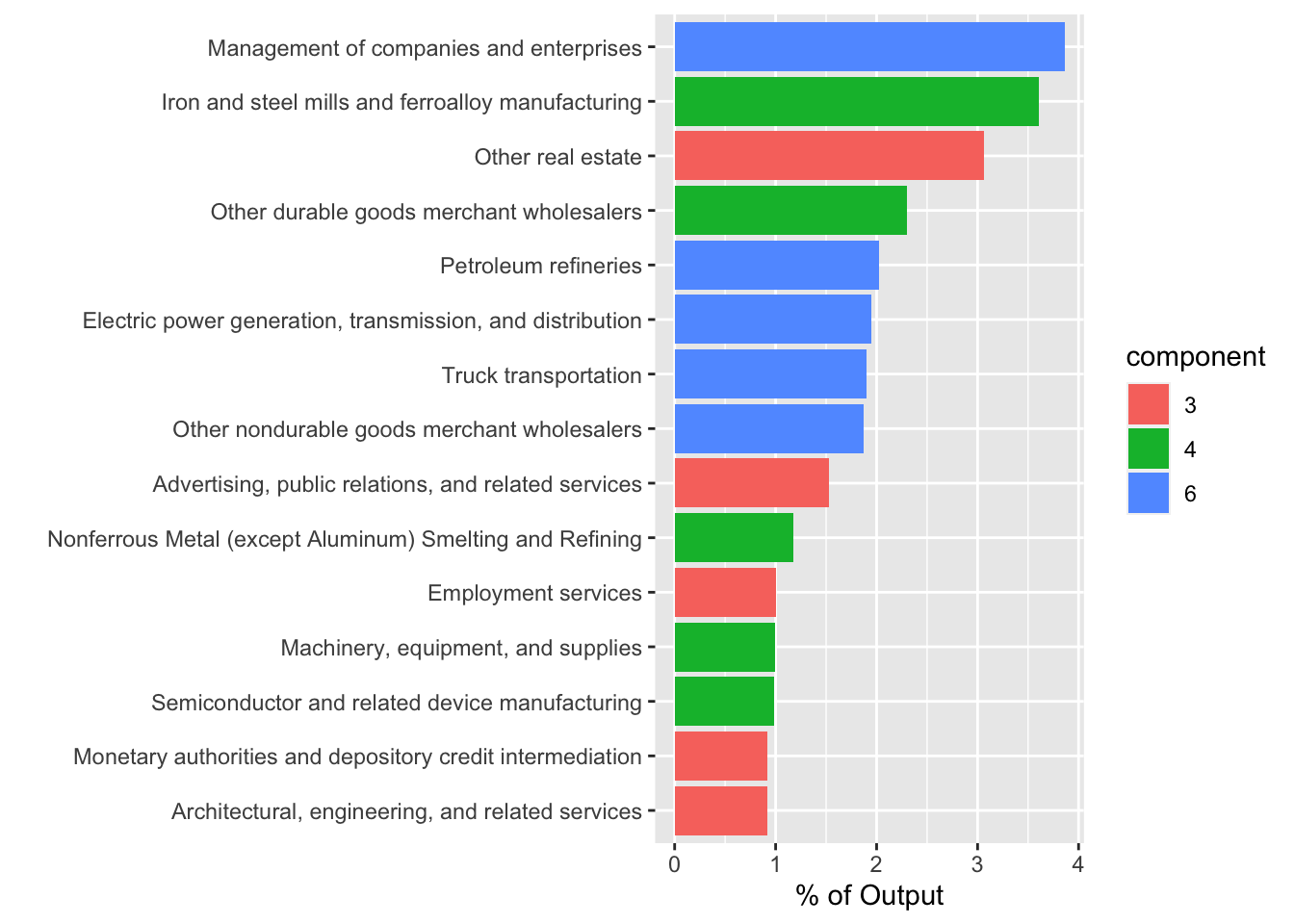

# + scale_fill_manual("component", values = rainbow_hcl(8, end = 290)[c(1,2,6,8)])

library(colorspace)
library(qgraph)

io.table.1 <- io.table
diag(io.table.1) <- 0
g <- graph_from_adjacency_matrix(io.table.1, mode = 'directed', weighted = TRUE, add.rownames = TRUE)

e <- get.edgelist(g, names = FALSE)
l <- qgraph.layout.fruchtermanreingold(e, vcount = vcount(g))
V(g)$size <- 5 * go ^ 0.25
V(g)$frame.color <- NA

V.cols <- member
V(g)$color <- alpha(rainbow_hcl(8, end = 290)[V.cols],0.8)
E(g)$color <- alpha('black', E(g)$weight / max(E(g)$weight))
V(g)$label <- NA


par(mar = c(0,0,0,0))

l <- qgraph.layout.fruchtermanreingold(e, vcount = vcount(g),
                                       area = 100 * (vcount(g) ^ 2), repulse.rad = (vcount(g) ^ 3))
# pdf('test.pdf') # uncomment to generate a pdf file with the plot
plot(g,layout = l, edge.arrow.size = 0)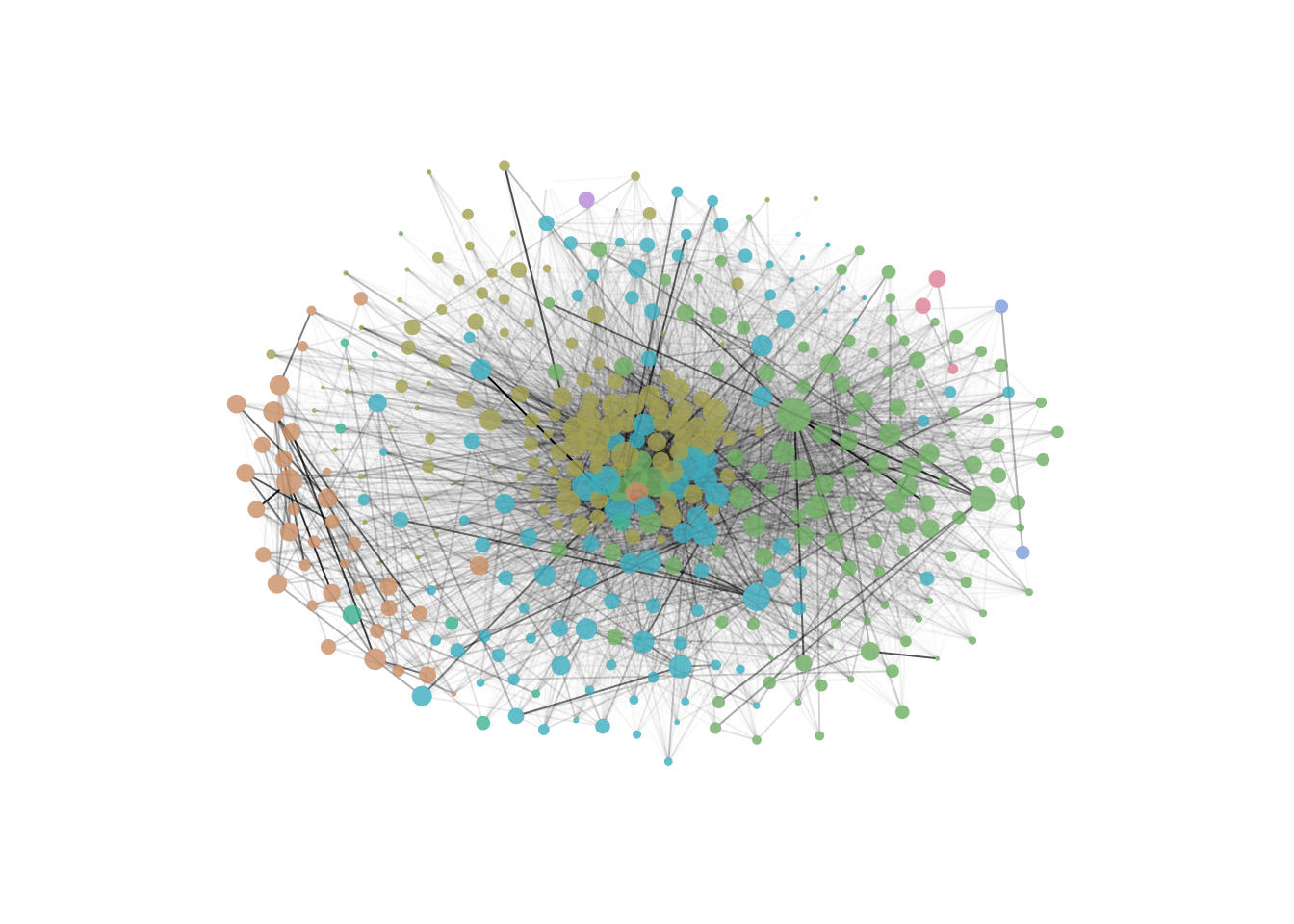

# dev.off() # uncomment to generate a pdf file