Code
library(tidyverse)
library(igraph)
library(statnet)
library(gssr)
library(drat)
knitr::opts_chunk$set(echo = TRUE)My dataset uses results from the 1985 General Social Survey. The data frame is based on “talkto,” which provides weighted edges based on members a respondent’s group of contacts. Weights are based on respondents’ perception of how much each contact talks to each other.
Skipping install of 'gssr' from a github remote, the SHA1 (abe949b1) has not changed since last install.
Use `force = TRUE` to force installationFetching: https://gss.norc.org/documents/stata/1985_stata.zipties <- gss85[,grepl("talkto", colnames(gss85))]
mat = matrix(nrow = 5, ncol = 5)
mat[lower.tri(mat)] <- as.numeric(ties[3,])
mat[upper.tri(mat)] = t(mat)[upper.tri(mat)]
na_vals <- is.na(mat)
non_missing_rows <- rowSums(na_vals) < nrow(mat)
mat <- mat[non_missing_rows,non_missing_rows]
diag(mat) <- 0
ig.net <- graph.adjacency(mat, mode = "undirected", weighted = T)Results show that there is 1 component and the median weight is 2.This network contains 5 vertices and 10 edges. Ties are not bipartite or directed but they are weighted.
[1] 1 Min. 1st Qu. Median Mean 3rd Qu. Max.
1.0 2.0 2.0 1.8 2.0 2.0 [1] 5[1] 10[1] FALSE[1] FALSE[1] TRUEIn the following tests I compare our networks network degree centralization, betweeness centrality, and transitivity with random networks to establish potential significance. These test let us determine if our sampled ego network is representative of the population in terms of important indicators of network characteristics. Doing so will help us establish the significance of any further tests such as on tie strength. Such tests will enable us to shed light on the attitudes of the network’s nodes as interpersonal attitudes are strong influences of unit formation (Heider, F. (1946). Attitudes and cognitive organization.).
To test our null hypothesis that our network’s transitivity is higher or lower than expected compared to a random network we can use a CUG-test. First we test transitivity conditioned on network size. Results show that we should accept the alternative hypothesis that the observed transitivity is higher than expected compared to a random network.
Univariate Conditional Uniform Graph Test
Conditioning Method: size
Graph Type: digraph
Diagonal Used: FALSE
Replications: 1000
Observed Value: 1
Pr(X>=Obs): 0.005
Pr(X<=Obs): 1 
Error in cug.t(trans.cug): could not find function "cug.t"If we instead test transitivity conditioned on dyads we get similar results and reject the null hypothesis.
Univariate Conditional Uniform Graph Test
Conditioning Method: dyad.census
Graph Type: digraph
Diagonal Used: FALSE
Replications: 1000
Observed Value: 1
Pr(X>=Obs): 1
Pr(X<=Obs): 1 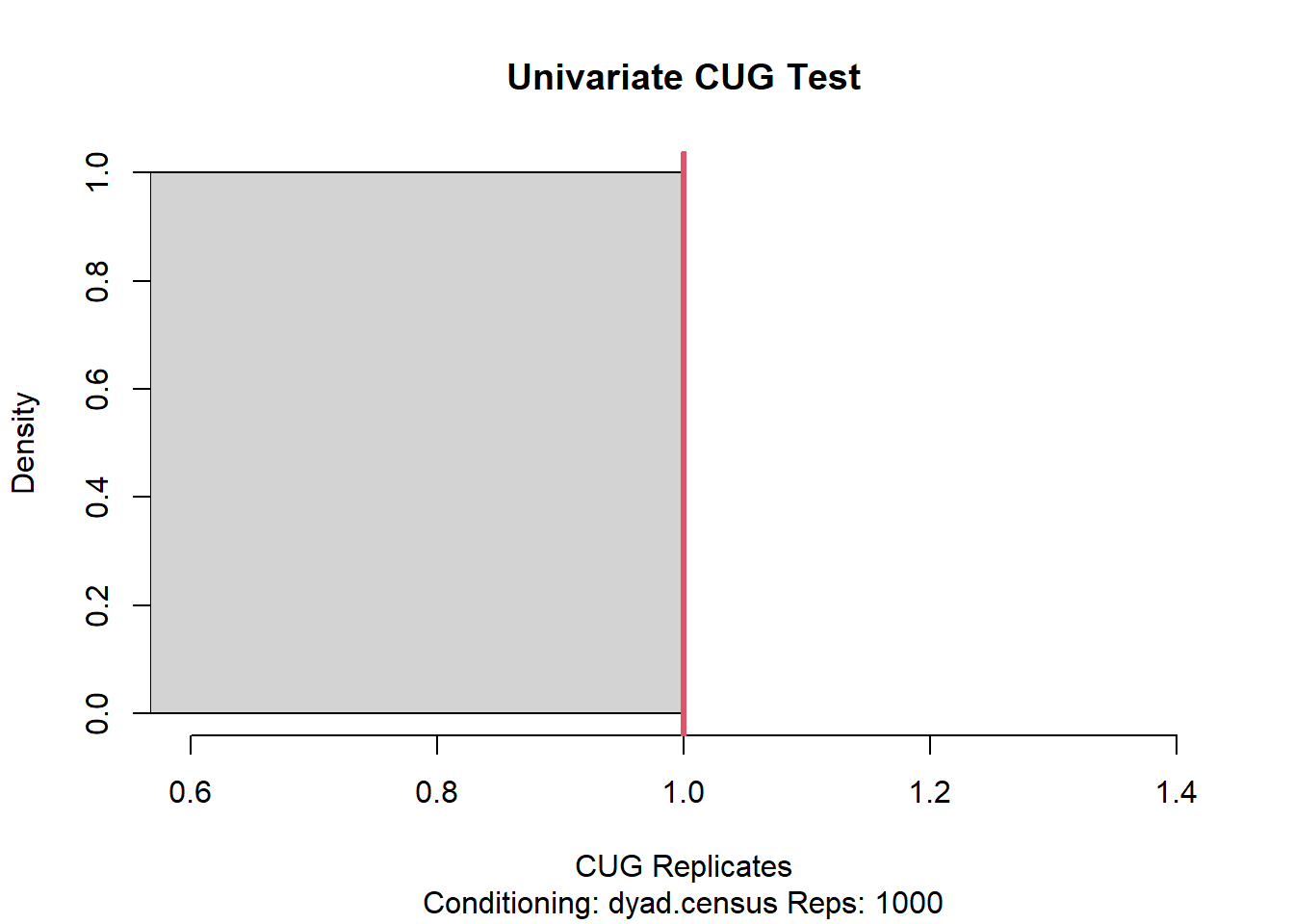
Error in cug.t(trans.cug): could not find function "cug.t"Alternatively, test transitivity can also be conditioned on edges which results in a similar outcome.
Univariate Conditional Uniform Graph Test
Conditioning Method: edges
Graph Type: digraph
Diagonal Used: FALSE
Replications: 100
Observed Value: 1
Pr(X>=Obs): 1
Pr(X<=Obs): 1 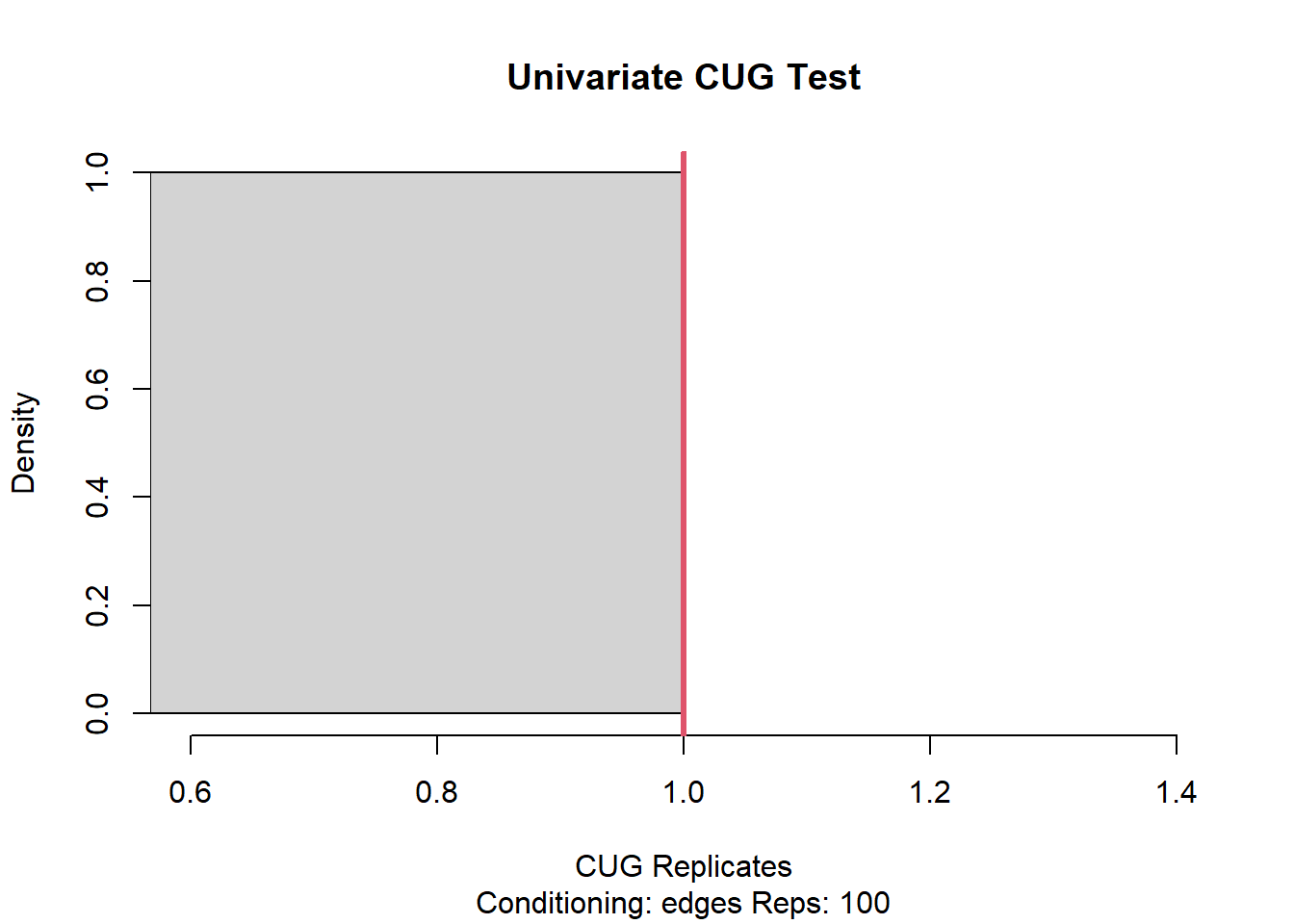
Error in cug.t(trans.cug): could not find function "cug.t"We can also test network degree centralization to the null conditional based on size. In this case, results indicate that we cannot reject the null hypothesis for network degree centralization. The t-statistic results show a score of -.62.
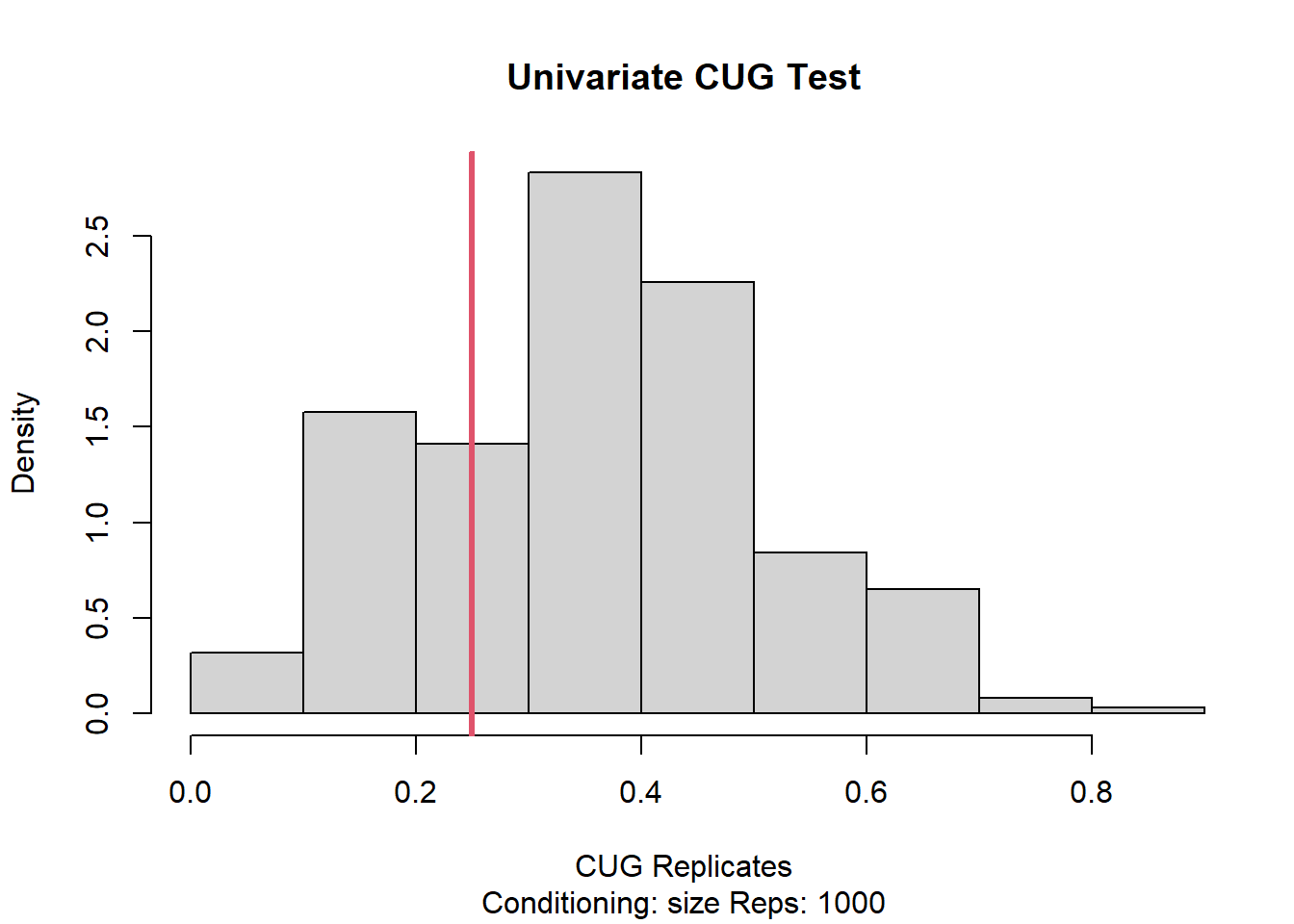
Error in cug.t(c.degree.cug): could not find function "cug.t"Here we test betweeness centrality with 100 reps. Results show that we should accept the alternative hypothesis that the observed betweeness centrality is lower than expected compared to a random network.
---
title: "WK9Challenge_KDocekal"
output: html_document
format:
html:
toc: true
code-fold: true
code-copy: true
code-tools: true
---
```{r, message=FALSE}
#| label: setup
#| warning: false
library(tidyverse)
library(igraph)
library(statnet)
library(gssr)
library(drat)
knitr::opts_chunk$set(echo = TRUE)
```
My dataset uses results from the 1985 General Social Survey. The data frame is based on "talkto," which provides weighted edges based on members a respondent's group of contacts. Weights are based on respondents' perception of how much each contact talks to each other.
```{r}
remotes::install_github("kjhealy/gssr")
drat::addRepo("kjhealy")
gss85 <- gss_get_yr(1985)
ties <- gss85[,grepl("talkto", colnames(gss85))]
mat = matrix(nrow = 5, ncol = 5)
mat[lower.tri(mat)] <- as.numeric(ties[3,])
mat[upper.tri(mat)] = t(mat)[upper.tri(mat)]
na_vals <- is.na(mat)
non_missing_rows <- rowSums(na_vals) < nrow(mat)
mat <- mat[non_missing_rows,non_missing_rows]
diag(mat) <- 0
ig.net <- graph.adjacency(mat, mode = "undirected", weighted = T)
```
Results show that there is 1 component and the median weight is 2.This network contains 5 vertices and 10 edges. Ties are not bipartite or directed but they are weighted.
```{r}
igraph::components(ig.net)$no
summary(E(ig.net)$weight)
vcount(ig.net)
ecount(ig.net)
is_bipartite(ig.net)
is_directed(ig.net)
is_weighted(ig.net)
```
In the following tests I compare our networks network degree centralization, betweeness centrality, and transitivity with random networks to establish potential significance. These test let us determine if our sampled ego network is representative of the population in terms of important indicators of network characteristics. Doing so will help us establish the significance of any further tests such as on tie strength. Such tests will enable us to shed light on the attitudes of the network's nodes as interpersonal attitudes are strong influences of unit formation (Heider, F. (1946). Attitudes and cognitive organization.).
To test our null hypothesis that our network's transitivity is higher or lower than expected compared to a random network we can use a CUG-test. First we test transitivity conditioned on network size. Results show that we should accept the alternative hypothesis that the observed transitivity is higher than expected compared to a random network.
```{r}
trans.cug<-cug.test(mat,FUN=gtrans,mode="digraph",cmode="size")
trans.cug
plot(trans.cug)
cug.t(trans.cug)
```
If we instead test transitivity conditioned on dyads we get similar results and reject the null hypothesis.
```{r}
trans.cug<-cug.test(mat,FUN=gtrans,mode="digraph",cmode="dyad")
trans.cug
plot(trans.cug)
cug.t(trans.cug)
```
Alternatively, test transitivity can also be conditioned on edges which results in a similar outcome.
```{r}
trans.cug<-cug.test(mat,FUN=gtrans,mode="digraph",cmode="edges", reps=100)
trans.cug
plot(trans.cug)
cug.t(trans.cug)
```
We can also test network degree centralization to the null conditional based on size. In this case, results indicate that we cannot reject the null hypothesis for network degree centralization. The t-statistic results show a score of -.62.
```{r}
c.degree.cug <-cug.test(mat,FUN=centralization, FUN.arg=list(FUN=degree, cmode="indegree"), mode="digraph", cmode="size")
plot(c.degree.cug)
cug.t(c.degree.cug)
```
Here we test betweeness centrality with 100 reps. Results show that we should accept the alternative hypothesis that the observed betweeness centrality is lower than expected compared to a random network.
```{r}
b.degree.cug <-cug.test(mat,FUN=centralization, FUN.arg=list(FUN=betweenness, cmode="directed"), mode="digraph", cmode="size", reps=100)
plot(b.degree.cug)
cug.t(b.degree.cug)
```